《九日集训》第十五轮 第三天(第三讲) 一维数组
知识点
数组
//int *nums和int nums[]等价
int add(int *nums, int numsSize) {
// ...
}
题目分析
题目1
分析
先找出数组是在哪个下标开始旋转的,由题目可知,数组在\([0,k]\),\([k+1,nums.size()-1]\)这段区间是升序的。然后与\(nums[0]\)比较,判断\(target\)在哪个区间,进行二分。要注意数组长度为\(1\)和\(nums\)是本来就是升序的情况
代码
class Solution {
public:
int search(vector<int>& nums, int target) {
//特殊情况,判断一下
if(nums.size()==1){
if(nums[0]==target)return 0;
else return -1;
}
int l,r;
for(int i=0;i<nums.size()-1;i++){
//判断数组在哪里开始旋转
if(nums[i]>nums[i+1]){
if(target<nums[0]){
l=i+1,r=nums.size()-1;
}else if(target>nums[0]){
l=0,r=i;
}else{
return 0;
}
break;
}else{
//升序排序
l=0,r=nums.size()-1;
}
}
//二分
while(l<=r){
int mid=l+r>>1;
if(nums[mid]>target)r=mid-1;
else if(nums[mid]<target)l=mid+1;
else return mid;
}
return -1;
}
};
题目2
分析
思路和上面那题相同,把上面的代码的返回值改一下,-1改成\(false\),其他改成\(true\)就行了( ̄▽ ̄)~*
代码
class Solution {
public:
bool search(vector<int>& nums, int target) {
//特殊情况,判断一下
if(nums.size()==1){
if(nums[0]==target)return true;
else return false;
}
int l,r;
for(int i=0;i<nums.size()-1;i++){
//判断数组在哪里开始旋转
if(nums[i]>nums[i+1]){
if(target<nums[0]){
l=i+1,r=nums.size()-1;
}else if(target>nums[0]){
l=0,r=i;
}else{
return true;
}
break;
}else{
//升序排序
l=0,r=nums.size()-1;
}
}
//二分
while(l<=r){
int mid=l+r>>1;
if(nums[mid]>target)r=mid-1;
else if(nums[mid]<target)l=mid+1;
else return true;
}
return false;
}
};
题目3
分析
必须是\(\log x\)的复杂度,明显是用二分。先判断一下数组是不是升序,如果不是的话与\(nums[0]\)比较,\(nums[mid]\)大的话说明最小值一定在左部分,反之一定在右部分。
代码
class Solution {
public:
int findMin(vector<int>& nums) {
//判断是否是升序
if(nums[0]<nums[nums.size()-1])return nums[0];
int l=0,r=nums.size()-1;
//二分
while(l<r){
int mid=l+r>>1;
if(nums[mid]<nums[0])r=mid;
else l=mid+1;
}
return nums[l];
}
};
题目4
分析
设\(a_n\)为第\(n\)层的方案数,因为既可以从第\(n-1\)层爬过来,也可以从第\(n-2\)层爬过来,当\(n=0\)和\(n=1\)时,方案显然只有一种,所以可以得知\(a_n\)满足
\[a_n=a_{n-1}+a_{n-2},其中a_1=1,a_2=1
\]
代码
class Solution {
public:
int f[46];
int climbStairs(int n) {
f[0]=f[1]=1;
for(int i=2;i<=n;i++){
f[i]=f[i-1]+f[i-2];
}
return f[n];
}
};
题目5
分析
斐波那契数,思路同上题,递推公式一样
代码
class Solution {
public:
int f[31];
int fib(int n) {
f[0]=0,f[1]=1;
for(int i=2;i<=n;i++){
f[i]=f[i-1]+f[i-2];
}
return f[n];
}
};
题目6
分析
思路同上两题。递推公式
\[T_{n+3}=T_{n+2}+T_{n+1}+T_n
\]
代码
class Solution {
public:
int f[40];
int tribonacci(int n) {
f[0]=0,f[1]=1,f[2]=1;
for(int i=3;i<=n;i++){
f[i]=f[i-1]+f[i-2]+f[i-3];
}
return f[n];
}
};
题目7
分析
本质上是找是满足\(nums[i]=k\pm nums[j]\)的\(num[i]\)个数
,所以用哈希表解决
答案
class Solution {
public:
int countKDifference(vector<int>& nums, int k) {
unordered_map <int,int> map;
int res=0;
for(auto num :nums){
if(map.count(num+k))res+=map[num+k];
if(map.count(num-k))res+=map[num-k];
map[num]++;
}
return res;
}
};
题目8
分析
枚举判断一下即可
代码
class Solution {
public:
int game(vector<int>& guess, vector<int>& answer) {
int counts=0;
for(int i=0;i<guess.size();i++){
if(answer[i]==guess[i])counts++;
}
return counts;
}
};
题目9
分析
当\(n\)为奇数时,最小次数为\(\frac{n+1}{2}\),当n为偶数时,最小次数为\(\frac{n}{2}\)
代码
class Solution {
public:
int minCount(vector<int>& coins) {
int res=0;
for(auto coin:coins){
res+=(int)(coin+1)/2;
}
return res;
}
};
题目10
分析
看到\(O(\log n)\)的时间复杂度,八成用二分,所以先写出模板
int l=0,r=arr.size()-1;
while(l<r){
int mid=(l+r+1)>>1;
if(check(mid))l=mid;
else r=mid-1;
}
return l;
然后因为这个数组是左增右减的,所以当\(arr[mid]>arr[mid-1]\),则一定在右区间,反之则在左区间
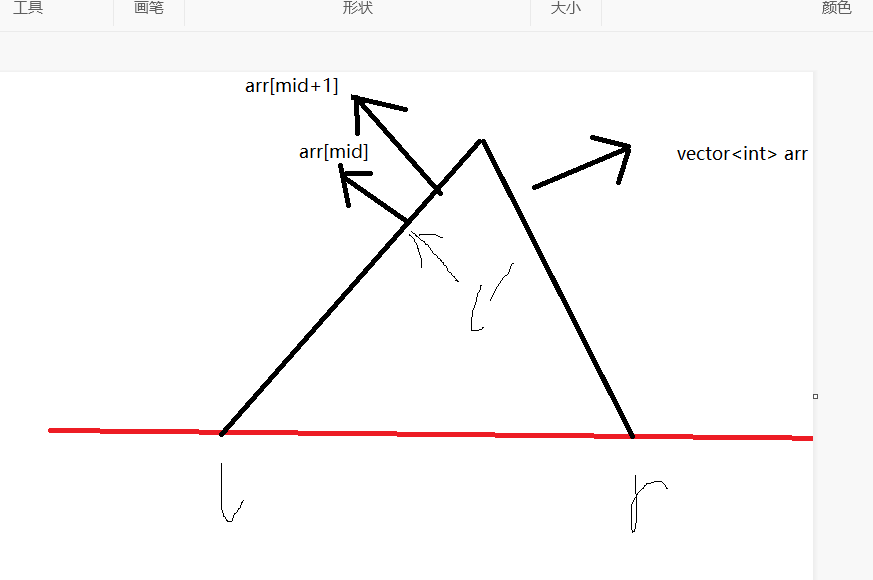
代码
class Solution {
public:
int peakIndexInMountainArray(vector<int>& arr) {
int l=0,r=arr.size()-1;
while(l<r){
int mid=(l+r+1)>>1;
if(arr[mid]>arr[mid-1])l=mid;
else r=mid-1;
}
return l;
}
};
总结
对于双指针和哈希这块感觉不熟练,对于2006. 差的绝对值为 K 的数对数目这题的优化方法想了俩小时,感觉自己太菜了qwq




 浙公网安备 33010602011771号
浙公网安备 33010602011771号