《九日集训》第15轮 第一天（第一讲）函数

知识点

函数

函数类型 函数名称(){
    //函数体
    ....
    return 返回值;
}

题目分析

题目1~3

371. 两整数之和

面试题 17.01. 不用加号的加法

剑指 Offer 65. 不用加减乘除做加法

分析

这三题的话计组课上讲过

​ \(a+b=(a\&b)<<1+a\)^\(b\)

\(a\)^\(b\)是不进位加法，\((a\&b)<<1\)表示进位。

由于题目里面要求不用加号，所以递归一下就行了。实际error了，应该是\(int\)类型左移报错，所以要转成\(unsigned\)类型

代码

class Solution {
public:
    int add(int a, int b) {
        if(!a)return b;
        int temp1=a^b;
        int temp2=(unsigned)(a&b)<<1;
        return add(temp2,temp1);
    }
};

题目4

面试题 08.05. 递归乘法

分析

$ a\times b=a+a \times (b-1)$

\(a \times (b-1) =a+a \times (b-2)=a+a \times [(b-1)-1]\)

....

很明显的递归关系

代码

class Solution {
public:
    int multiply(int A, int B) {
        if(B==0)return 0;
        if(B==1)return A;
        return A+multiply(A,B-1);
    }
};

题目5

29. 两数相除

分析

没想出来，氵过去，要注意当\(a=-2^{31}\)，\(b=-1\)时会溢出

代码

class Solution {
public:
    int divide(int a, int b){
        if(a == -2147483648 && b == -1) {
            return 2147483647;            
        }
        return a / b;  
    }                   
};

题目6

50. Pow(x, n)

分析

快速幂算法

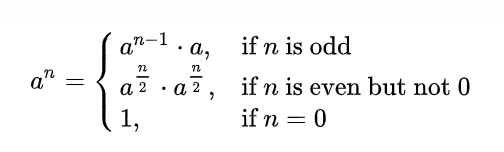
模板如下：

//泛型的非递归快速幂
template <typename T>
T qpow(T a, ll n)
{
    T ans = 1; // 赋值为乘法单位元，可能要根据构造函数修改
    while (n)
    {
        if (n & 1)
            ans = ans * a; // 这里就最好别用自乘了，不然重载完*还要重载*=，有点麻烦。
        n >>= 1;
        a = a * a;
    }
    return ans;
}

这里要注意考虑n为负数的情况

代码

class Solution {
public:
    double myPow(double x, int n) {
        double ans=1;
        long long N;
        if(n>0){
            N=(long long)n;
        }else{
            N=-(long long)n;
        }
        while(N>0){
            if(N&1)ans=ans*x;
            N>>=1;
            x=x*x;
        }
        return n<0?1/ans:ans;
    }
};

题目7

69. x 的平方根

分析

明显二分，需要注意当\(x=1\)的特殊情况。

代码

class Solution {
public:
    int mySqrt(int x) {
        if(x==1)return 1;
        int l=0,r=x;
        const double eps=1; //精度
        while(r-l>1){
            int mid=(r+l)/2;
            if(mid>x/mid) r=mid;
            else l=mid;
        }
        return l;
    }
};

题目8

面试题 16.07. 最大数值

分析

没想出来，假装自己做出来了qwq

代码

class Solution {
public:
    int maximum(int a, int b) {
        return max(a,b);
    }
};

题目9

2119. 反转两次的数字

分析

当\(num=0\)或者尾数不为\(0\)的时候，反转两次数字一定是\(true\)，反正一定是\(false\)，所以只需要判断一下尾数到底是不是\(0\)。

代码

class Solution {
public:
    bool isSameAfterReversals(int num) {
        if(num==0)return true;
        if(num%10)return true;
        return false;
    }
};

总结

有些题要想的时间有些久，还是要多加练习qwq，另题：
29. 两数相除
面试题 16.07. 最大数值
以后一定补票。