数据结构-概述及线性表

# 数据结构概述

数据结构的定义

• 数据结构是指数据元素的集合及其元素之间的相互关系
• 数据结构中，元素之间的相互关系称为数据的逻辑结构，元素及元素之间关系在计算机中的存储形式称为数据的存储结构或物理结构
• 数据结构按逻辑结构不同分为线性结构和非线性结构两大类，常见的线性结构有线性表、栈和队列，常见的非线性结构有树、图等。

线性表、链表

线性表的定义

• 一个线性表是一个由n个元素组成的有限序列。线性表中元素的个数n为线性表的长度，长度为0的线性表称为空表。非空线性表这种线性结构由如下特点
• 存在唯一一个被称为"第一个"的数据元素
• 存在唯一一个被称为"最后一个"的数据元素
• 除第一个之外，集合中的每个数据元素均只有一个直接前驱
• 除最后一个之外，集合中的每个数据元素均只有一个直接后继

线性表的存储结构

• 主要有两种存储方式：顺序存储和链接存储
• 通常用一个数组来实现顺序存储，从数组的第一个元素开始，将线性表的元素依次存储在数组中，即线性表的第i个结点存储数组的第i个元素中，用数组元素的顺序存储来体现线性表中元素的先后次序关系
  
• 链接存储中，用结点来存储元素，结点空间在需要时才分配不必事先分配号。最基本的结点结构中有两个域：数据域和指针域，如下图：
  
• 顺序存储和链接存储优缺点比较:
  

栈、队列

栈的定义

• 只允许在同一端进行插入和删除操作的线性表称为栈，允许插入和删除的一端称为栈顶，另一端称为栈底。栈具有后进先出的特征。
  

队列的定义

• 只允许在表的一端插入元素而在另一端删除元素的线性表称为队列，其具有先进后出的特性。只允许插入元素的一端称为队尾(rear),只允许删除元素的一端称为队友(front)
  

循环队列

• 在顺序队列中，当尾指针到达数组上界时就不能插入新的元素了，而此时数组的实际可用空间并未满。此时，可通过整除取余运算"rear=(rear+1)%m"将顺序队列假想成一个环状结构，称为循环队列
  

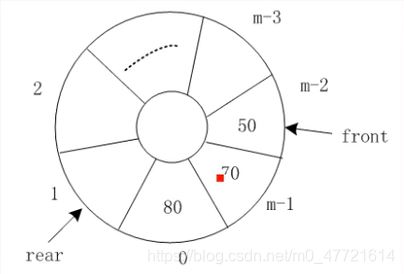
循环队列队空、队满的标志

• 跟顺序队列一样，当front=rear时表明队列为空。但是若在循环队列中不采取特殊措施，当其队满时，front和rear也相等，为了区分这两者，要牺牲一个元素空间，约定"rear"所指位置的环上的下一个位置是front时,表示队列满，即：front==(rear+1)%m
  

数组、稀疏矩阵

数组的定义

• n维数组是一种"同构"的数据结构，其中的每个元素类型相同，结构一致。数组是定长线性表上的扩展，即线性表中的元素又是一个线性表。

二维数组的存储

• 二维数组的存储结构分为以行为主序和以列为主序两种方式

地址计算

• 二维数组A[m][n]若按行优先存储，那么A的任意一个元素A[i][j]的存储地址Loc(i,j)可由下式确定:
  Loc(i,j)=Loc(0,0)+(ni+j)b
  其中，Loc(0,0)是第一个元素A[0][0]的首地址，b是每个元素占用的存储单元个数
• 按列优先存储就是把二维数组的数据一列一列地顺次存入存储单元。二维数组A[m][n]若按行优先存储，那么A的任意一个元素A[i][j]的存储首地址Loc(i,j)可由下式确定:
  Loc(i,j)=Loc(0,0)+(mj+i )b

稀疏矩阵的定义、存储

• 在一个矩阵中，若非零元素的个数远小于零元素的个数，而且非零元素分布没有规律，则称该矩阵为稀疏矩阵

字符串

字符串的基本概念

• 字符串是由某字符集上的字符所组成的任何有限字符序列
• 当一个字符串不包含任何字符时，称它为空串
• 一个字符串所包含的有效字符个数称为这个字符串的长度
• 一个字符串中任一连续的子序列称为该字符串的子串。空串是任意串的子串。比如，"by"是"passerby"的子串
• 由一个或多个空格组成的串称为空格串。虽然空格是一个空白字符，但是他也是一个字符，计算串长时要将其计算在内

字符串的比较

• 两个字符串比较大小时以字符的ASCLL码值作为依据，从第一个字符开始比较，若第一个相等，则取第二个继续比较，字符的ASCLL码值大的所在的串大，若其中一个串先结束，则后结束的串较大。若全部相同，则认为这两串相等
• 在字母表中，越靠后ASCLL码值越大，同一字母的小写字母的ASCLL码值比大写字母的ASCLL码值大