数值的整数次方
Q:实现函数double Power(double base, int exponent),求base的exponent次方。不需要考虑溢出。
A:这是一道很简单的题,但是考虑全面和优化代码却不是那么容易,一开始乍一看可能就写出这样的代码
double Power(double base,int exponent)
{
double result=1.0;
for(int i=0;i<exponent;++i)
result*=base;
return result;
}
这样的代码只能给人以不严谨的感觉,因为考虑并不全面。因为exponent是一个整数,所以可能为正也有可能为负,同时base也有可能为0,我们要全面考虑才行。改进后的代码如下
double Power(double base,int exponent)
{
//不合法输入,对于这种输入直接输出0
if(isZero(base) && exponent<0)
return 0.0;
unsigned int unsignedexp=static_cast<unsigned int>(exponent);
if(exponent<0)
unsignedexp=static_cast<unsigned int>(-exponent);
double result=PowerWithUnsignedExponent(base,unsignedexp);
if(exponent<0)
result=1.0/result;
return result;
}
double PowerWithUnsignedExponent(double base,unsigned int exponent)
{
double result=1.0;
for(int i=0;i<exponent;++i)
result*=base;
return result;
}
改进后的算法考虑了不合法的输入,同时也考虑了指数为负数的情况,考虑情况已经全面。但是还是有改进的空间。
我们可以将指数拆分成2的各次幂的加法,然后利用c^(a+b)=c^a*c^b,则可以有效减少乘法的次数。
double PowerWithUnsignedExponent(double base,unsigned int exponent)
{
std::bitset<32> bits(exponent);
if(bits.none())
return 1.0;
int num=bits.count();
double mutiplication[32];
for(int i=0;i<32;++i)
multiplication[i]=1.0;
int count=0;
double power=1.0;
for(int i=0;i<32 && count <num;++i)
{
if(i==0)
power=base;
else
power=power*power;
if(bits.at(i))
{
multiplication[i]=power;
++count;
}
}
power=1.0;
for(int i=0;i<32;++i)
if(bits.at(i))
power*=multiplication[i];
return power;
}
我们用递归的思路进行考虑,可以得出公式
则递归的算法为
double PowerWithUnsignedExponent(double base,unsigned int exponent)
{
if(exponent==0)
return 1.0;
if(exponent==1)
return base;
double result=PowerWithUnsignedExponent(base,exponent/2);
result*=result;
if(exponent & 0x1==1)
result*=base;
return result;
}
参考自:http://zhedahht.blog.163.com/blog/static/254111742009101563242535/


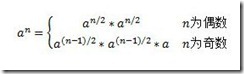

 浙公网安备 33010602011771号
浙公网安备 33010602011771号