模拟费用流

模拟费用流简单来说就是，使用除了最短路以外更加快速的过程进行增广，并不是一个很高深的知识点。

模拟费用流有三种流派，这里每一种拉出来几道例题作为介绍。

消环

拿最大费用流（流量不一定最大）举例：费用流需要每一次找到一条最长路，事实上如果不找最长路也可以求费用流。每一次将一条边加入到残余网络中，可能出现正环或者增广路，选取其中权值较大者增广即可。

CF865D Buy Low Sell High

题目描述

你完美预测了股票接下来 \(n\) 天的价格。在接下来的 \(n\) 天，你每天可以选择什么都不干，买入一股或者卖出一股。起初你没有股票，并且你希望最后一天你也不持有任何股票，求出最大的可能盈利。

\(1 \leq N \leq 10^5\) 。

题解

“每天可以选择什么都不干，买入一股或者卖出一股”的限制，我们不喜欢，我们改成“每一天可以选择什么都不干，可以买入，也可以同时卖出” 。因为一支股票在同一天买入并且卖出和什么都不干是等价的。

考虑一个费用流建模:

• 原点向每一天连流量为 \(1\) ，费用为 \(-a_i\) 的边，表示买入。
• 第 \(i\) 天向第 \(i+1\) 天连流量为 \(inf\) ，费用为 \(0\) 的边。
• 每一天向汇点连流量为 \(1\) ，费用为 \(a_i\) 的边，表示卖出。

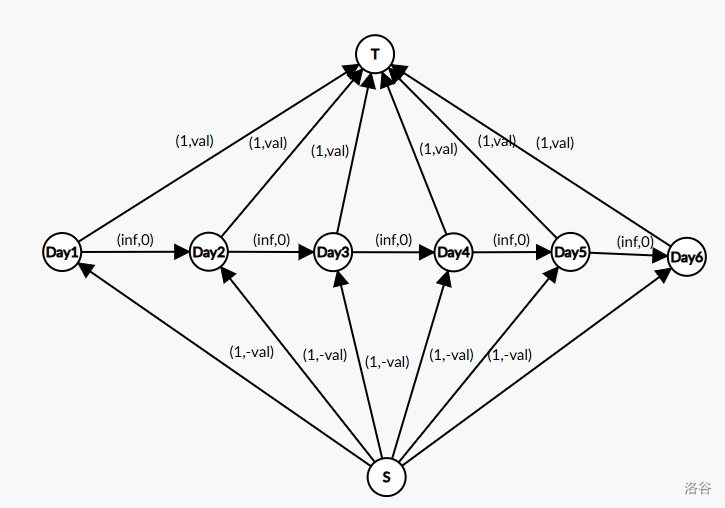
我们按照第一天到第 \(n\) 天的顺序去考虑，每一次分别加入 \(S\rightarrow i\) 和 \(i \rightarrow T\) 两条边。

首先正环是不可能同时经过 \(S,T\) 两个节点的，不然会出现增广路。

当我们加入 \(S\rightarrow i\) 的时候不会出现正环，因为 \(i \rightarrow i-1\) 的边现在没流量，所以根本形成不了环，自然也形成不了最短路。

接下来加入 \(i \rightarrow T\) 的边就可能出现增广路和正环了。增广路的形式应该是 \(S \rightarrow j \rightarrow i \rightarrow T (j<i)\) ，正环的形式应该是 \(T \rightarrow j \rightarrow i \rightarrow T(j<i)\) 。我们只需要在两者中取一个较优者就可以了。分析一下这两种情况，发现 \(j \rightarrow i \rightarrow T\) 的部分是一定可以完成了，我们只关心 \(S \rightarrow j\) 和 \(T \rightarrow j\) 的部分。

关于这两种情况的维护可以使用一个大根堆，堆的内部维护了 \(S \rightarrow j\) 和 \(T \rightarrow j\) 的所有情况。

每一次，先往看看堆顶加上 \(a_i\) 是否为正，如果为正那么 \(i \rightarrow T\) 这条边就会被使用，产生 \(T \rightarrow i\) 的情况，需要将 \(-a_i\) 加入堆中。由于 \(S \rightarrow i\) 的边本身存在，还需要将 \(-a_i\) 加入堆中。

代码好写，并且和大家熟知的反悔贪心做法是完全一样的。

#include<bits/stdc++.h>
#define int long long
using namespace std;
const int MAXN=3e5+5;
int n,ans,a[MAXN];
priority_queue<int> q;
signed main(){
	cin>>n;
	for(int i=1;i<=n;i++){
		cin>>a[i];
		if(!q.empty()&&q.top()+a[i]>0){
			ans+=q.top()+a[i];
			q.pop();
			q.push(-a[i]);
		}
		q.push(-a[i]);
	}
	cout<<ans;
	return 0;
}

P9168 [省选联考 2023] 人员调度

题目描述

众所周知，一个公司的 \(n\) 个部门可以组织成一个树形结构。形式化地，假设这些部门依次编号为 \(1, \ldots, n\)，那么除了 \(1\) 号部门以外，第 \(i \in [2, n]\) 个部门有且仅有一个上级部门 \(p_i \in [1, i - 1]\)。这样，这家公司的 \(n\) 个部门可以视为一个以 \(1\) 为根的树。如果 \(i\) 是 \(j\) 子树中的点，那么称部门 \(i\) 是部门 \(j\) 的子部门。

该公司初始时有 \(k\) 名优秀员工，编号依次为 \(1 \ldots k\)。第 \(i\) 名优秀员工初始时在第 \(x_i\) 个部门工作，并且其有一个能力值 \(v_i > 0\)。

为了最大化公司的运作效率，公司老板 0/\/\G 决定进行一些人员调动。具体来说，可以将编号为 \(i\) 的优秀员工调动到 \(x_i\) 的一个子部门，或者不调度（此时该员工在 \(x_i\) 部门）。随后，优秀员工们会在其所在的部门竞选部门领导——能力值最高者将担任这一职位，并给公司带来等同于其能力值的贡献。如果一个部门一个优秀员工也没有，那么就无法选出部门领导，从而对公司的贡献将是 \(0\)。此时，公司的业绩被定义为公司各部门的贡献之和。

公司老板 0/\/\G 自然想知道，该如何进行人员调动，使公司的业绩最大？

这当然难不倒他，然而，公司优秀员工的数量也会发生变化；具体来说，会依次发生 \(m\) 个事件，每个事件形如：

• 1 x v：先令 \(k = k + 1\)，然后新增一位编号为 \(k\)、初始部门为 \(x\)、能力值为 \(v\) 的优秀员工；
• 2 id：编号为 \(\mathit{id}\) 的优秀员工将被辞退。

公司老板 0/\/\G 希望你能在最开始和每个事件发生后，告诉他公司的业绩最大可能是多少？

注意，每次人员调动都是独立的，也就是每次计算公司的最大可能业绩时，每个优秀员工都会回到其所在的初始部门。

\(1 \leq n,m,k \leq 10^5\) 。\(5s\) 。

题解

不考虑两种操作，看看怎么解决这个问题。

考虑一个建模：

• 对于树上的 \(n\) 个节点，如果 \(j\) 是 \(i\) 的父亲，那么连 \(j\) 向 \(i\) 连流量为 \(inf\) ，费用为 \(0\) 的边。
• 建立超级汇点，对于树上的每一个节点，向汇点 \(T\) 连流量为 \(1\) ,费用为 \(0\) 的边。
• 对于一个初始部门为 \(x\) ，能力为 \(v\) 的优秀员工，超级源点 \(S\) 向 \(x\) 连流量为 \(1\) ，费用为 \(0\) 的边。

直接跑最大费用流（流量不一定最大但是费用最大）就是答案了。考虑优化这个过程。

先加入树上的每一条边，以及他们到汇点的边。此时不出现任何增广路或者正环。

接下来以此加入每一位优秀员工。然后考虑增广路和正环分别是什么样子的。增广路的形态是显然的，\(S \rightarrow i \rightarrow j \rightarrow T\) 。正环考虑到一定经过 \(S \rightarrow i\) ，那么形式也一定是 \(S \rightarrow i \rightarrow j \rightarrow S\) 。

我们怎么知道 \(i\) 可以到达的 \(j\) 有哪些呢？其实很简单，不断向父亲走，直到不存在父亲或者向父亲的边没有流量即可。假设现在走到了节点 \(k\) ，那么 \(k\) 子树内的所有点都是可以增广的。

如果 \(k\) 子树内存在某一个节点，它走到 \(T\) 的路径没有被使用过，我们直接增广。因为本题中如果同时存在增广路和正环，增广路的权值一定大。

如果子树内所有节点到 \(T\) 的路径都已经被增广过了，就只能找到子树内能力值最小的，被增广的优秀员工，看看形成的环是否是一个正环，如果是的就消去这个正环。

不要忘记增广/消环后将使用的边反向。

现在我们得到了一个 \(O(n^2)\) 的算法，但是容易使用数据结构优化到 \(O(n \log n)\) 。无非是 \(LCT\) 或者全局平衡二叉树一类数据结构。

原问题还有员工加入和员工删除。如果只有员工加入没有任何影响，因为这种费用流算法根本不care边的加入顺序。但是员工删除产生的影响就很大了，我们可以使用线段树分治把删除改为撤销，代价是时间复杂度多一只 $\log $ 。

总体时间复杂度 \(O(n \log^2 n)\) ,代码这里不放了。

使用数据结构找出最短路

P4694 [PA 2013] Raper

题目描述

你需要生产 \(k\) 张光盘。每张光盘都要经过两道工序：先在 A 工厂进行挤压，再送到 B 工厂涂上反光层。

你知道每天 A、B 工厂分别加工一张光盘的花费。你现在有 \(n\) 天时间，每天可以先送一张光盘到 A 工厂（或者不送），然后再送一张已经在 A 工厂加工过的光盘到 B 工厂（或者不送），每家工厂一天只能对一张光盘进行操作，同一张光盘在一天内生产出来是允许的。我们假定将未加工的或半成品的光盘保存起来不需要费用。

求生产出 \(k\) 张光盘的最小花费。

保证 \(1 \leqslant k \leqslant n \leqslant 5 \times 10^5,\) \(1 \leqslant a_i, b_i \leqslant 10^9\)。

题解

这个题目的主流做法是wqs二分优化dp做法，需要 \(O(n \log n \log V)\) 的时间还只能够求解单个 \(k\) 。但是存在一种 \(O(n + k \log n)\) 的模拟费用流算法，可以求解出所有的 \(k\) 。这种做法挺实用但是复杂性较高，有点容易忘（UNR的时候我就忘记了但是不好意思去翻写过的代码）。

考虑一个费用流建模：

• 源点向代表第 \(i\) 天的节点连流量为 \(1\) ，费用为 \(a_i\) 的边。
• 第 \(i\) 天向第 \(i+1\) 天连流量为 \(inf\) ，费用为 \(0\) 的边。
• 第 \(i\) 天向汇点连流量为 \(1\) ，费用为 \(b_i\) 的边。

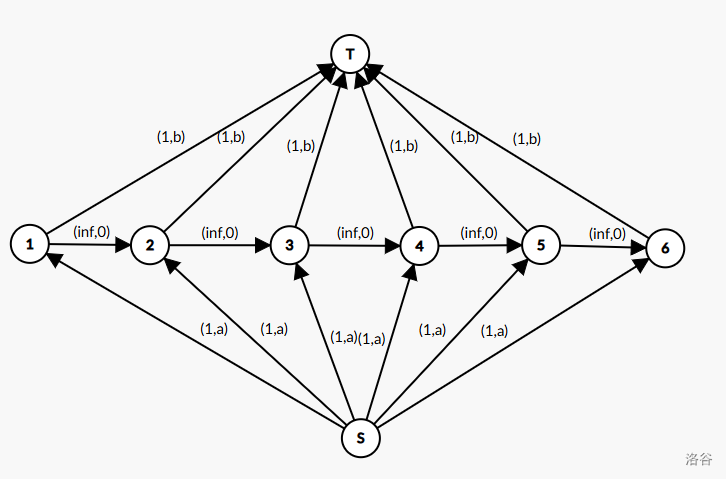
每一次增广我们都尝试找到最短路，分为两种情况：\(S \rightarrow i \rightarrow j \rightarrow T (i<j)\) 和 \(S \rightarrow i \rightarrow j \rightarrow T (i>j)\) 。

其中第一种情况一定合法，比较容易维护。重点是第二种情况，他要求对于每一条 \(k+1\) 天连向第 \(k\) 天的边都有流量才行 \((j \leq k < i)\) 。

我们尝试使用线段树解决这个问题，由于增广之后有对边流量的区间加或者区间减，让 \(j,i\) 之间不存在流量为 \(0\) 的边相当困难（区间打标记的影响很大）。但是我们尝试维护这样的信息：

• 区间反边流量的最小值 \(mn\) 。
• 区间加标记 \(tag\) 。
• 二元组 \((x0,y0)\) 满足 \(x0\leq y0\) 并且 \(a_{x0}+b_{y0}\) 最大。
• 二元组 \((x1,y1)\) 满足 \(x1>y1\) 并且 \(a_{x1}+b_{y1}\) 最大。
• 二元组 \((x2,y2)\) 满足 \(x2>y2\) 并且 \(a_{x2}+b_{y2}\) 最大,同时还要满足在 \(y2,x2\) 之间的反边流量要严格大于这个区间反边流量的最小值。
• \(mna\) 表示区间 \(a\) 的最小值所在的下标。
• \(mnb\) 表示区间 \(b\) 的最小值所在的下标。
• \(pre\) 表示区间内 \(a\) 的最小值所在的下标，但是要求 \(a\) 到区间最左端的所有反边的流量都要严格大于这个区间反边流量的最小值。
• \(suf\) 表示区间内 \(b\) 的最小值所在的下标，但是要求 \(b\) 到区间最右端的所有反边的流量都要严格大于这个区间反边流量的最小值。

发现这样不仅比较容易 pushup ，并且在 pushdown 的时候只会影响 \(mn,tag\) 。这种定义的好处就是，我们让不存在流量为 \(0\) 的限制和区间最小值挂钩，区间整体加减的影响就少。

那么现在就解决了这个问题，这个线段树还比较厉害。

放一份 pushup 的代码：

struct node{
	int x[3],y[3];
	int mna,mnb;
	int suf,pre;
	int mn,tag;
}t[MAXN<<2];
void pushup(int &x,int &y,int p,int q){
	if(a[x]+b[y]>a[p]+b[q]) x=p,y=q;
}
void pushup(int i){
	int ls=i<<1,rs=i<<1|1;
	
	t[i].mn=min(t[ls].mn,t[rs].mn);
	
	if(a[t[ls].mna]<a[t[rs].mna]) t[i].mna=t[ls].mna;
	else t[i].mna=t[rs].mna;
	if(b[t[ls].mnb]<b[t[rs].mnb]) t[i].mnb=t[ls].mnb;
	else t[i].mnb=t[rs].mnb;
	
	t[i].suf=t[rs].suf;
	if(t[rs].mn>t[i].mn){
		if(b[t[i].suf]>b[t[rs].mnb]) t[i].suf=t[rs].mnb;
		if(b[t[i].suf]>b[t[ls].suf]) t[i].suf=t[ls].suf; 
	}
	t[i].pre=t[ls].pre;
	if(t[ls].mn>t[i].mn){
		if(a[t[i].pre]>a[t[ls].mna]) t[i].pre=t[ls].mna;
		if(a[t[i].pre]>a[t[rs].pre]) t[i].pre=t[rs].pre;
	}
	
	for(int j=0;j<3;j++){
		t[i].x[j]=t[i].y[j]=0;
		pushup(t[i].x[j],t[i].y[j],t[ls].x[j],t[ls].y[j]);
		pushup(t[i].x[j],t[i].y[j],t[rs].x[j],t[rs].y[j]);
	}
	pushup(t[i].x[0],t[i].y[0],t[ls].mna,t[rs].mnb);
	pushup(t[i].x[1],t[i].y[1],t[rs].mna,t[ls].mnb);
	pushup(t[i].x[2],t[i].y[2],t[rs].pre,t[ls].suf);
	if(t[ls].mn>t[i].mn){
		pushup(t[i].x[2],t[i].y[2],t[ls].x[1],t[ls].y[1]);
		pushup(t[i].x[2],t[i].y[2],t[rs].pre,t[ls].mnb); 
	}
	if(t[rs].mn>t[i].mn){
		pushup(t[i].x[2],t[i].y[2],t[rs].x[1],t[rs].y[1]);
		pushup(t[i].x[2],t[i].y[2],t[rs].mna,t[ls].suf); 
	}
}