杂题选做1

杂题选做1

[ARC112F] Die Siedler

注意到如果存在某一个 \(j\) 满足这种牌的数量大于等于 \(2j\) ，那么一定会兑换为 \(j \bmod n +1\) 的牌。所以我们考虑这个过程的逆过程，就是将一张牌 \(j\) 换成 \((j-1)!2^{j-1}\) 张 \(1\) 号牌，最终全部的牌都被转化为了 \(1\) 号牌，但是结果并不会改变。记录 \(P=\sum_{i=1}^n c_i 2^{i-1} (i-1)!\) ，表示初始局面 \(1\) 号牌的数量。同理记录 \(b_k=\sum_{i=1}^n a_{k,i}2^{i-1}(i-1)!\) 表示牌堆 \(k\) 经过转化后的 \(1\) 号牌数量。

考虑一组选取牌堆的方案 \(x_1,x_2,\dots,x_n (x_i \geq 0)\) ,最终的 \(1\) 号牌数量为 \(Q=P+\sum_{i=1}^n x_ib_i\) 。这个值可能很大，但是考虑我们将 \(1\) 号牌换成 \(2\) 号牌 ，一直换直到又合成了一张 \(1\) 号牌，中间减少了 \(2^nn!\) 张牌，但是又获得了一张牌。所以 \(Q\) 和 \(Q \bmod (2^nn!-1)\) 是等价的。定义 \(f(Q)\) 表示初始拥有 \(Q(Q <2^nn!)\) 张 \(1\) 号牌，最终会剩下多少牌，具体计算只需要 \(O(n)\) 模拟一下即可。

考虑什么样的 \(Q\) 是可以被表示出来的？那么根据

\[Q \equiv P+\sum_{i=1}^nx_ib_i (\bmod 2^nn!-1) \]

得到

\[Q-P \bmod (2^nn!-1)=\sum_{i=1}^n x_ib_i - y\times (2^nn!-1) \]

记录 \(d=\gcd(b_1,b_2,\dots,b_n,2^nn!-1)\) ，最终一定需要满足 \(Q-P\bmod (2^nn!-1) =kd\) ，因为 \(d\) 是 \(2^nn!-1\) 的因数，所以这又是 \(Q=kd+P\bmod d\) 。

考虑一个比较有意思的事情，因为有效的 \(Q<2^nn!-1\) 的缘故，\(kd<2^nn!-1\) ，那么 \(k \leq \frac{2^nn!-1}{d}\) ，当 \(d\) 比较大的时候有比较快的速度。\(O(n\frac{2^nn-1}{d})\) 。

那么 \(d\) 比较小的时候怎么办？我们考虑随意填写卡牌，只需要最终全部的卡牌转化为 \(1\) 号牌后，模 \(d\) 的余数为 \(P \bmod d\) 即可，这个过程可以使用同余最短路处理。\(O(nd)\) 。

这个容易想到根号分治。

事实上，在 \(\sqrt{2^nn!-1}\) 以内的 \(d\) 最大为 \(1615037\) 。显而易见的第二种做法符合了时间复杂度。考虑第一种做法的时间最大消耗是啥？\(O(n\frac{2^nn!-1}{1615037})\) 吗？并不是的。第一个大于 \(\sqrt{2^nn!-1}\) 的因数就是 \(e=\frac{\sqrt{2^nn!-1}}{1615037}\) ，带入第一种做法得到时间最劣为 \(O(1615037n)\) ，可以通过。

[ABC348G] Max (Sum - Max)

首先肯定将元素按照 \(B_i\) 升序排列，接下来发现不好做了。因为当 \(\max\{B_i\}\) 变大的时候我们不好对于每一个 \(k\) 去更新答案和历史最优答案。

性质：记录 \(f_i\) 表示 \(k=i\) 的时候，最优解中 \(\max\{B\}\) 的值，则 \(f_i\geq f_{i-1}\) 。

证明:假设存在两个 \(i,j\) 使得 \(i<j,f_i > f_j\) 。我们可以选取 \(j\) 最优解中 \(A\) 前 \(i\) 大的元素，这样一定比 \(i\) 原来的方案减去的 \(\max\{B\}\) 小，并且 \(\sum A\) 不会变小。

所以我们可以考虑决策单调性，问题转化为如何快速求出 \(f(i,j)\) 表示考虑按照 \(B\) 排序后的前 \(i\) 个元素，选取 \(j\) 个元素使得 \(\sum A\) 最大？我们可以建立主席树，那么这个问题就是前缀前 \(k\) 大的元素和类似问题，容易 \(O(\log n)\) 求解。

时间复杂度 \(O(n \log ^ 2 n)\) 。

[ARC111F] Do you like query problems?

答案是求和，所以我们可以对于每一个位单独考虑。就是求 \(\sum a_i\) ，不过取 \(\min\) 取 \(\max\) 的操作让维护权值具有一定难度，所以我们转化为 \(\sum_{1 \leq d <m} \sum [a_i \geq d]\) 。

现在考虑一个 \(d\) 如何求出贡献？我们再枚举一个位置 \(p\) 以及询问的时间 \(i\) ，考虑如果在询问的时候 \(a_p \geq d\) ，需要满足什么条件，我们找到 \(i\) 之前最近的一次取 \(\max\) 操作(\(l \leq p \leq r\))且 \(v \geq d\) ，假设是第 \(j\) 次操作。那么在操作 \((i,j)\) 之间就不可以出现 \(v<d\) 的取 \(\min\) 操作 \((l \leq p \leq r)\)。

综上，我们枚举 \(d,p,i,j\) 四个变量，然后列出如下公式：

设 \(A=\frac{n(n+1)}{2}(2m+1)\) ，这是一次操作在没有任何限制下的总方案数。

\[\sum_{d=1}^{m-1}\sum_{p=1}^n\sum_{i=1}^q \sum_{j=1}^{i-1} A^{j-1}A^{q-i} p^2(n-p+1)^2(m-d)(A-p(n-p+1)m)^{i-j-1} \]

给出一个解释：

• \(A^{j-1}A^{q-i}\) ，这是表示在操作 \(j\) 和询问 \(i\) 之后的操作可以随意做。
• \(p^2(n-p+1)^2(m-d)=[p(n-p+1)]\times [p(n-p+1)(m-d)]\) 。其中 \(p(n-p+1)\) 表示第 \(i\) 次询问的时候，包含 \(p\) 的询问区间总数；\(p(n-p+1)(m-d)\) 表示第 \(j\) 次取 \(\max\) 操作的方案数，\(m-d\) 是因为要求 \(v \geq d\) 。
• \((A-p(n-p+1)m)^{i-j-1}\) 表示 \((i,j)\) 之间的操作的方案数。考虑求出不合理的那些操作有哪些？一定是包含 \(p\) 的区间，所以具有 \(p(n-p+1)\) 的系数。注意到 \(v <d\) 的 \(\min\) 操作不合法，有 \(d\) 种可能性；\(v \geq d\) 的取 \(\max\) 操作不合法，因为违背了 \(j\) 是 \(i\) 操作之前第一个 \(v \geq d\) 的取 \(\max\) 操作的定义，所以有 \(m-d\) 种可能性。一共就是 \(m\) 种可能性。

现在这个公式是 \(O(n^4)\) 的，我们逐步优化。

优化1

注意到公式和 \(d\) 关联的不过只有 \(m-d\) ，记录 \(B=\sum_{d=1}^{m-1}(m-d)\) ,原式等价于:

\[B\sum_{p=1}^n\sum_{i=1}^q \sum_{j=1}^{i-1} A^{j-1}A^{q-i} p^2(n-p+1)^2(A-p(n-p+1)m)^{i-j-1} \]

现在优化到了 \(O(n^3)\) 。

优化2

将和 \(i,p\) 有关的式子分离出第三个循环，则：

\[B\sum_{p=1}^np^2(n-p+1)^2\sum_{i=1}^q A^{q-i-1}(A-p(n-p+1)m)^{i-1}\sum_{j=1}^{i-1} A^{j} (A-p(n-p+1)m)^{-j} \]

最后一个循环如果令 \(C=A(A-p(n-p+1)m)^{-1}\) ，则就是一个等比序列求和

\[B\sum_{p=1}^np^2(n-p+1)^2\sum_{i=1}^q A^{q-i-1}(A-p(n-p+1)m)^{i-1}C\times \dfrac{1-C^{i-1}}{1-C} \]

现在优化到了 \(O(n^2)\) 。

优化3

发现 \(C\) 和 \(i\) 是无关的，我们将仅和 \(C\) 有关的提出去

\[B\sum_{p=1}^np^2(n-p+1)^2\sum_{i=1}^q A^{q-i-1}(A-p(n-p+1)m)^{i-1} \dfrac{C-C^{i}}{1-C} \]

\[B\sum_{p=1}^np^2(n-p+1)^2A^{q-1}\dfrac{1}{1-C}(A-p(n-p+1)m)^{-1}\sum_{i=1}^q A^{-i}(A-p(n-p+1)m)^{i}(C-C^{i}) \]

前面的一坨是系数，我们不关心。我们拿出后面的式子出来看：

\[\sum_{i=1}^q A^{-i}(A-p(n-p+1)m)^{i}(C-C^{i}) \]

拆分为两个部分：

\[\sum_{i=1}^q A^{-i}(A-p(n-p+1)m)^{i}C \]

还有

\[-\sum_{i=1}^q A^{-i}(A-p(n-p+1)m)^{i}C^{i} \]

第一部分是一个等比序列求和，第二部分也是一个等比序列求和。

所以被优化到了 \(O(n \log mod)\) ，因为快速幂需要时间。

[CF875F] Royal Questions

给出一个十分自然的做法，可能吧。

这个题目很容易想到带权二分图匹配，因为数据规模过大，考虑使用模拟费用流的手段解决。

建模比较简单：

• 源点向公主 \(i\) 连流量为 \(1\) ，费用为 \(0\) 的边。

• 公主 \(i\) 连向一个辅助节点 \(v_i\) ，费用为 \(w_i\) ，流量为 \(1\) 。

• 辅助节点 \(v_i\) 连向 \(a_i,b_i\) 两位王子表示的节点，费用为 \(0\) ，流量为 \(1\) 。

• 王子 \(i\) 向汇点连流量为 \(1\) ，费用为 \(0\) 的边。

对于第一个样例，建模如下：

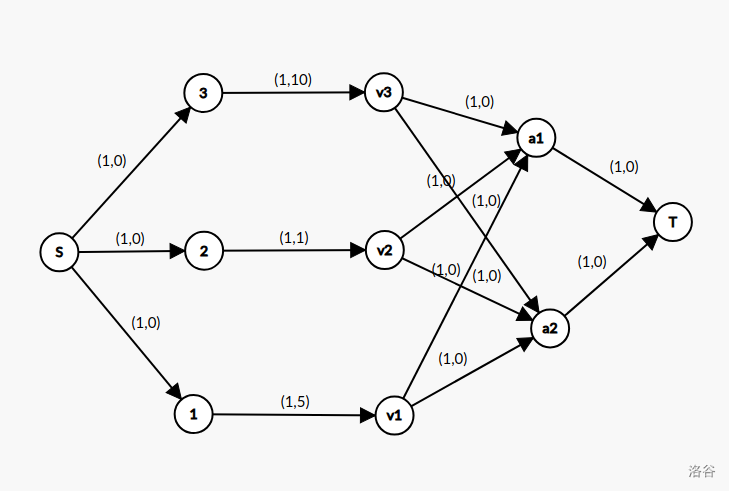
跑最大费用最大流就是答案了。

我们分析每一次找到的增广路的形态。

• 因为过程中不会出现正权环，所以没有必要经过相同的节点两次。这一点十分重要，意味着流一旦到达了 \(v_i\) 就不会回头。

• 整张图有非 \(0\) 费用的边只有 \(i\) 连向 \(v_i\) 的这些边，也就是说一旦到达 \(v_i\) 就决定了整条路径的费用。

既然如此，我们可以将公主们按照 \(w_i\) 从大到校排序，能增广就增广。

考虑第一次增广带来的影响。原来是这样的：

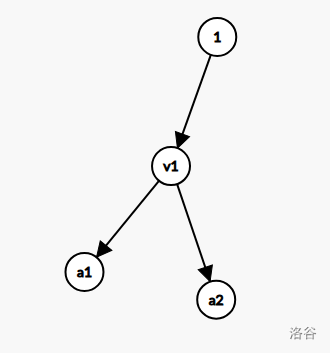
假设增广的时候选择了 \(a_1\) ，其实 \(a_2\) 也行，那么网络就变成了这样：

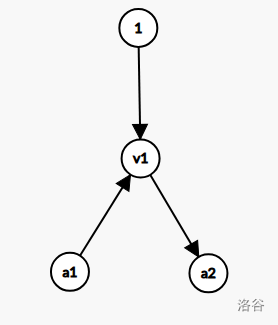
注意到此时 \(a_1\) 到汇点的边已经没有流量了，不会被再次经过。所以一个点一旦到达了 \(a_1\) ，就只能经过 \(v_1\) 从 \(a_2\) 走出去。

并且因为 \(1\) 公主已经被增广，所以 \(v_1\) 到 \(a_2\) 的边不会被 \(1\) 公主再次使用，所以可以直接忽略 \(a_1\) 到 \(v_1\) ，\(v_1\) 到 \(a_2\) 两条边。转而添加一条 \(a_1\) 到 \(a_2\) 的边，记录通过这种方式得到的边为二类边。

我们观察到一个十分重要的性质（其实也很好发现，手玩一下样例即可），就是 二类边在任意时刻构成的图等价于一棵树 。这是为什么呢？假设不是一棵树：

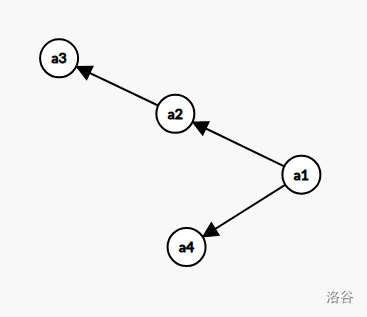
假设产生 \(a_1,a_4\) 这条边的时候，\(a_1,a_2,a_3\) 之间的边已经存在了。如果 \(a_3\) 可以增广到汇点，那么 \(a_1\) 到 \(a_2\) , \(a_2\) 到 \(a_3\) 之间的这些边应当被反向，变成下图：

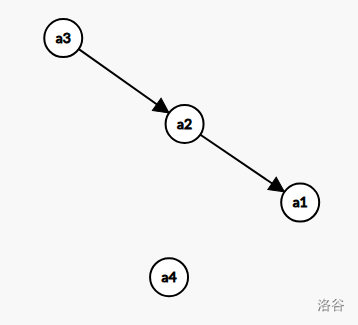
如果 \(a_3\) 到汇点的边已经被使用过了，那么这位公主就会直接增广 \(a_4\) ，从而产生一条 \(a_4\) 到 \(a_1\) 的边。那也不是一棵树。

所以任意时刻二类边都应该是一棵树才对。

具体流程就是对于嫁妆从大到小的每一位公主：

分别考虑 \(a_i,b_i\) 两位王子是否存在一位满足一下条件之一：

• 直接到达汇点。

• 通过二类边走到一个可以到达汇点的节点。

如果是第一种情况是容易处理的，直接添加一条 \(a_i,b_i\) 之间的二类边即可。

但是如果是第二种呢？会产生什么影响？通过对于“二类边构成的图等价于一棵树”的证明时使用的图，你就会发现影响就是将一条到根的路径反向。给出一个更具一般性的例子。

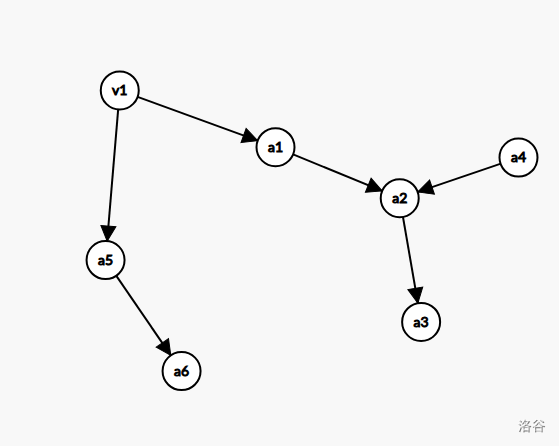
其中公主 \(1\) 希望通过 \(a_1\) 到 \(a_3\) 的路径增广。在增广之后的二类边变成：

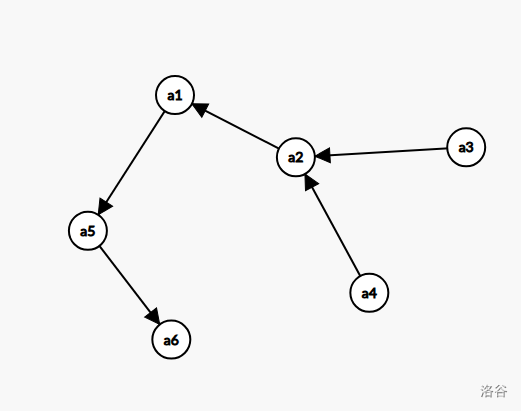
具体修改就是反向了 \(a_1\) 到 \(a_3\) 的路径，然后添加了 \(a_1\) 到 \(a_5\) 的二类边。这个操作属于动态树的基础操作，可以使用 \(\text{LCT}\) 维护但是没有必要。

有没有更简单的方法？

首先对于反向 \(a_1\) 到 \(a_3\) 的路径(其中 \(a_3\) 是根)，等价于将这棵树的根换到 \(a_1\) 。添加 \(a_1\) 到 \(a_5\) 的边等价于将根 \(a_1\) 的父亲设为 \(a_5\) 。那么以上的操作其实等价于将 \(a_3\) 的父亲设为 \(a_5\) 。

现在的问题就是如何找到某一位王子所在的内向树的根，使用并查集就可以了。上述将某个并查集的根的父亲设为另一个节点也是并查集的模板操作。

时间复杂度 \(O(n \log n)\) ，因为使用排序算法和并查集。

提醒：可能出现 \(a_i,b_i\) 处于同一个并查集的情况，注意判断。