高等数理统计知识点
Catalog:
- 弱大数定理 ------ 辛钦大数定理、伯努利大数定理、切比雪夫大数定理
- 中心极限定理、李雅普诺夫(Lyapunov)定理、棣莫弗-拉普拉斯(De Moivre-Laplace)定理
- 常见统计量:样本均值、样本方差、样本k阶矩、样本k阶中心矩、样本偏度系数、样本峰度系数
- 二项式分布
- 泊松分布 ------ Possion分布
- 正态分布 ------ normal(中心极限定理)
- Gamma分布族 ------ gamma函数、指数分布、卡方分布
- Beta分布族
- $F$分布
- 正态总体的样本均值和样本方差的方差
- Z分布族
- 学生氏分布 ------ t分布
- 评估量的平价指标:均方误差、无偏估计、相合性、渐近正态性
- 假设检验 ------ 基本概念、第一类错误、第二类错误、纽曼皮尔逊(Neyman—Pearson)显著性假设检验原则、假设检验的势函数、纽曼-皮尔逊(Neyman-Pearson)基本引理、一致最优势检验
大数定律
辛钦大数定理
设随机变量$X_{1},X_{2},\cdots $是独立同分布的,且具有数学期望$E\left ( X_{k} \right )= \mu \left ( k= 1,2,\cdots \right )$。作为前$n$个变量的算数平均$\frac{1}{n}\sum_{k=1}^{n}X_{k}$,则对于任意$\varepsilon > 0$,有:
$\lim_{n \to \infty }P\left \{ \left |\frac{1}{n}\sum_{k=1}^{n}X_{k}-\mu \right |< \varepsilon \right \}= 1$
或者称之为:序列$\bar{X}= \frac{1}{n}\sum_{k=1}^{n}X_{k}$依概率收敛于$\mu$,即$\bar{X}\overset{P}{\rightarrow}\mu $。
伯努利大数定理
设$f_{A}$是$n$次独立重复实验中事件$A$发生的次数,$p$是事件$A$在每次实验中发生的概率,对于任意$\varepsilon > 0$,有:
$\lim_{n \to \infty }P\left \{ \left |\frac{f_{A}}{n}-\mu \right |< \varepsilon \right \}= 1$
Chebyshev大数定律(切比雪夫大数定理)
设随机变量$X_{1},X_{2},\cdots ,X_{n}$是独立的(不要求同分布),且随机变量的方差$D\left ( X_{k} \right )$一致有上界。则有$\bar{X}= \frac{1}{n}\sum_{k=1}^{n}X_{k}$依概率收敛于$\frac{1}{n}\sum_{k=1}^{n}E\left (X_{k} \right )$。即:
$\frac{1}{n}\sum_{k=1}^{n}X_{k} \overset{P}{\rightarrow}\frac{1}{n}\sum_{k=1}^{n}E\left (X_{k} \right )$
中心极限定理
棣莫弗-拉普拉斯(De Moivre-Laplace)定理是中心极限定理的特殊情况,即分布为二项分布的中心极限定理。李雅普诺夫(Lyapunov)定理引入“二阶以上中心矩的期望和除以方差和”当$n \to \infty $时,它趋于$0$,以此将同分布推广到不限制分布。
独立同分布的中心极限定理
设随机变量$X_{1},X_{2},\cdots ,X_{n},\cdots $是独立同分布的,期望和方差分别为:$E\left ( X_{k} \right )= \mu ,D\left ( X_{k} \right )= \sigma ^{2}> 0 \left ( k= 1,2,\cdots \right )$。则随机变量之和$\sum_{k=1}^{n}X_{k}$的标准化变量
$Y_{n}= \frac{\sum_{k=1}^{n}X_{k}-E\left ( \sum_{k=1}^{n}X_{k} \right )}{\sqrt{D\left ( \sum_{k=1}^{n}X_{k} \right )}}= \frac{\sum_{k=1}^{n}X_{k}-n\mu }{\sqrt{n}\sigma }$
的分布函数$F_{n}\left ( x \right )$对任意$x$,有:
$\lim_{n \to \infty } F_{n}\left ( x \right )= \lim_{n \to \infty } P \left \{ \frac{\sum_{k=1}^{n}X_{k}-n\mu }{\sqrt{n}\sigma} \leq x \right \}\\ \qquad= \int_{-\infty }^{x}\frac{1}{\sqrt{2\pi} }e^{-\frac{t^{2}}{2}}dt\\ \qquad= \Phi \left ( x \right )$
其中是$\Phi \left ( x \right )$标准正态分布。
李雅普诺夫(Lyapunov)定理
设随机变量$X_{1},X_{2},\cdots ,X_{n},\cdots $是独立的,期望和方差分别为:$E\left ( X_{k} \right )= \mu_{k} ,D\left ( X_{k} \right )= \sigma_{k} ^{2}> 0 \left ( k= 1,2,\cdots \right )$,记$B_{n}^{2}= \sum_{k=1}^{n} \sigma _{k}^{2}$。若存在正数$\delta $,使得当时$n \to \infty $,
$\frac{1}{B_{n}^{2+\delta }}\sum_{k=1}^{n}E\left \{ \left | X_{k}-\mu _{k} \right |^{2+\delta } \right \}\rightarrow 0$
则随机变量之和$\sum_{k=1}^{n}X_{k}$的标准化变量
$Y_{n}= \frac{\sum_{k=1}^{n}X_{k}-E\left ( \sum_{k=1}^{n}X_{k} \right )}{\sqrt{D\left ( \sum_{k=1}^{n}X_{k} \right )}}= \frac{\sum_{k=1}^{n}X_{k}-\sum_{k=1}^{n}\mu_{k} }{B_{n}}$
的分布函数$F_{n}\left ( x \right )$对任意$x$,有:
$\lim_{n \to \infty } F_{n}\left ( x \right )= \lim_{n \to \infty } P \left \{ \frac{\sum_{k=1}^{n}X_{k}-\sum_{k=1}^{n}\mu _{k} }{B_{n}} \leq x \right \}\\ \qquad= \int_{-\infty }^{x}\frac{1}{\sqrt{2\pi} }e^{-\frac{t^{2}}{2}}dt\\ \qquad= \Phi \left ( x \right )$
棣莫弗-拉普拉斯(De Moivre-Laplace)定理
设随机变量$\eta _{n}\left ( n=1,2,\cdots \right )$服从参数为$n,p\left ( 0< p< 1 \right )$的二项分布,则对于任意$x$,有:
$\lim_{n \to \infty }P\left \{ \frac{\eta _{n}-np}{\sqrt{np\left ( 1-p \right )}} \leq x \right \}= \int_{-\infty }^{x}\frac{1}{\sqrt{2\pi} }e^{-\frac{t^{2}}{2}}dt\\ \qquad= \Phi \left ( x \right )$
常见统计量
样本均值:$\bar{X}=\frac{1}{n}\sum_{i=1}^{n}X_{i}$
样本方差:$s^{2}=\frac{1}{n-1}\sum_{i=1}^{n}\left ( X_{i}-\bar{X} \right )^{2}$
样本$k$阶矩:$A_{k}=\frac{1}{n}\sum_{i=1}^{n}X_{i}^{k},k=1,2,\cdots $
样本$k$阶中心矩:$B_{k}=\frac{1}{n}\sum_{i=1}^{n}\left (X_{i}-\bar{X} \right )^{k},k=1,2,\cdots $
样本偏度系数:$\beta _{1}= \frac{\sqrt{n}\sum_{i=1}^{n}\left (X_{i}-\bar{X} \right )^{3}}{\left [ \sum_{i=1}^{n}\left (X_{i}-\bar{X} \right )^{2} \right ]^{\frac{3}{2}}}$
样本偏度系数可以看作:$\beta_{1}= \frac{B_{3}}{\left (B_{2} \right )^{\frac{3}{2}}}$。样本偏度系数这个统计量描述的是样本分布的对称情况,若数据分布是对称的,$\beta_{1}$为$0$。若$\beta_{1}> 0$,则分布为右偏,有一条长尾在右;若$\beta_{1}< 0$,则分布为左偏,有一条长尾在左。同时偏度的模越大,说明分布的偏移程度越严重。
样本峰度系数:$\beta_{2}= \frac{n\sum_{i=1}^{n}\left (X_{i}-\bar{X} \right )^{4}}{\left [ \sum_{i=1}^{n}\left (X_{i}-\bar{X} \right )^{2} \right ]^{2}}-3$
样本峰度系数可以看作:$\beta_{2}= \frac{B_{4}}{\left (B_{2} \right )^{2}}-3$。样本峰度系数描述的是分布的平滑或陡峭程度的统计量,减去$3$是为什么呢?因为标准正态分布的峰度就是$0$,即:$\frac{B_{4}}{\left (B_{2} \right )^{2}}=3$,所以是将正态分布作为基准。
二项式分布
二项分布是由伯努利提出的概念,指的是重复n次独立的伯努利试验。基本假设条件为:重复实验之间相互独立。若单次实验成功的概率为p,失败为1-p,那么n次实验成功k次的概率为:
$\binom{n}{k}p^{k}\left ( 1-p \right )^{n-k}$
泊松分布
泊松分布在统计学的角度上可以看作二项式分布从离散到连续的推广。假设随机事件发生的时间超级短,我们认为它是瞬时发生的,且在时间轴上是连续的,那么从二项式分布的角度有如下思考:事件要么发生要么不发生,发生的概率为p,不发生的概率为1-p,假设我们将时间轴划分为n份,每一份发生概率为p,不发生概率为1-p,那么总共发生k次的概率为:
$P\left ( X= k \right )=\binom{n}{k}p^{k}\left ( 1-p \right )^{n-k}$
此时的时间轴是离散的,因为我们为了和二项式分布靠拢,分成了n份,如果n趋向于无穷大呢?首先p值会变小,因为区间越大,质量分布应该越大。对分割取极限有:
$P\left ( X= k \right )= \lim_{n \to \infty }\binom{n}{k}p^{k}\left ( 1-p \right )^{n-k}$
若n份切割的发生期望为$\mu $,那么我们可以将p写为$\frac{\mu }{n}$。上式可以分割为两部分的乘积:
$P\left ( X= k \right )= \lim_{n \to \infty }\binom{n}{k}\left (\frac{\mu }{n} \right )^{k}\cdot \lim_{n \to \infty }\left ( 1-\frac{\mu }{n} \right )^{n-k}$
其中:
$\lim_{n \to \infty }\binom{n}{k}\left (\frac{\mu }{n} \right )^{k}= \lim_{n \to \infty}\frac{\mu ^{k}}{k!}\frac{n}{n}\frac{n-1}{n}\cdots \frac{n-k+1}{n}= \frac{\mu ^{k}}{k!}$
$\lim_{n \to \infty }\left ( 1-\frac{\mu }{n} \right )^{n-k}= \lim_{n \to \infty}\left ( 1-\frac{\mu }{n} \right )^{n}\cdot \left ( 1-\frac{\mu }{n} \right )^{-k}= e^{-\mu }$
所以有,连续轴上发生k次的概率为:
$P\left ( X= k \right )= \frac{\lambda^{k}}{k!}\cdot e^{-\lambda}$
注意这里的$\lambda$和$\mu$是等价的,上式我们称之为泊松分布的分布率。
二项分布与泊松分布的关系
当n很大,p很小时,二项分布可以由泊松分布近似计算。
$P\left ( X= k \right )= \binom{n}{k}p^{k}\left ( 1-p \right )^{n-k}= \frac{\lambda^{k}}{k!}\cdot e^{-\lambda}$
参考文献:泊松分布的现实意义是什么,为什么现实生活多数服从于泊松分布?
正态分布
正态分布又名高斯分布,是自然界常见的一个分布。概率密度函数为:
$P\left ( x \right )= \frac{1}{\sqrt{2\pi}\sigma}e^{-\frac{\left ( x-\mu \right )^{2}}{2\sigma ^{2}}}$
中心极限定理:
假设随机变量$X_{1}$、$X_{2}$、$\cdots$、$X_{n}$、$\cdots$独立同分布,对于:
$F_{n}\left ( x \right )= P\left ( \frac{\sum_{i=1}^{n}X_{i}-n\mu }{\sigma \sqrt{n}} \leq x\right )$
有,当n趋向于无穷大时,$F_{n}\left ( x \right )$服从正态分布,即:$Y_{n}= \frac{\sum_{i=1}^{n}X_{i}-n\mu }{\sigma \sqrt{n}}$服从标准正态分布$N\left ( 0,1 \right )$。
Gamma分布族
Gamma分布族表示为:$Ga\left ( \alpha ,\lambda \right )$。其中$\alpha$为形状参数,$\lambda$为尺度参数。概率密度函数为:
$p\left ( x;\alpha, \lambda \right )= \frac{\lambda ^{\alpha }}{\Gamma\left ( \alpha \right ) }x^{\alpha -1}e^{-\lambda x}$
其中gamma函数为:$\Gamma\left ( \alpha \right )= \int_{0}^{+\infty }t^{\alpha -1}e^{-t}dt$,若n为正整数,则有$\Gamma\left ( n \right )= \left (n-1 \right )!$。当$0\leq \alpha \leq 1$时,概率密度函数是严格的递减函数;当$1< \alpha \leq 2$时,概率密度函数为先上凸,再下凸;当$\alpha > 2$时,概率密度函数为先下凸,再上凸,最后再下凸,此时有两个拐点。如图所示:
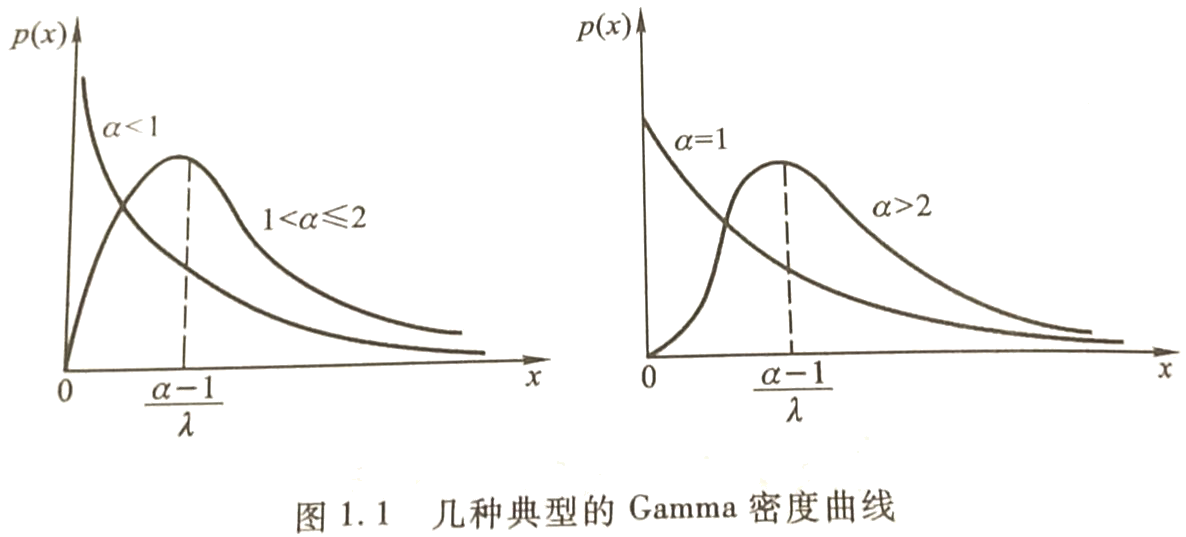
属于Gamma族的几种常见分布:
指数分布:当$\alpha = 1$时,概率密度函数为:$p\left ( x \right )= \lambda e^{-\lambda x}, x\geq 0$。
卡方分布:$Ga\left ( \frac{n}{2},\frac{1}{2} \right )= \chi ^{2}\left ( n \right )$。
在$\lambda$相同时,关于形状参数具有可加性:$Ga\left ( \alpha_{1},\lambda \right )+Ga\left ( \alpha_{2},\lambda \right )=Ga\left ( \alpha_{1}+\alpha_{2},\lambda \right )$。
Beta分布族
beta分布族的定义域为:$D=\left ( 0,1 \right )$,记为:$Be\left ( a,b \right )$。概率密度函数为:
$p\left ( x;a,b \right )= \frac{\Gamma \left ( a+b \right )}{\Gamma \left ( a \right )\Gamma \left ( b \right )}x^{a-1}\left ( 1-x \right )^{b-1}$
概率密度曲线如下图所示:
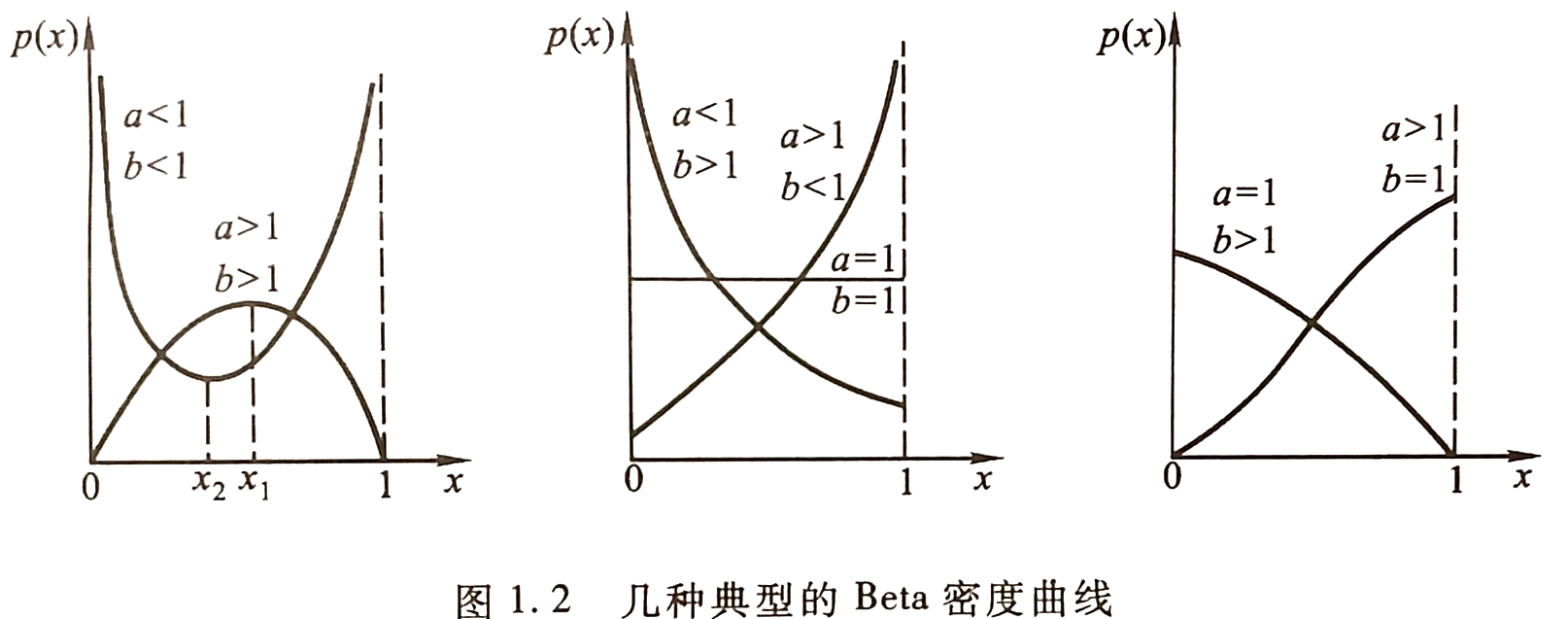
Beta变量$X$的$k$阶矩为:
$E\left ( X^{k} \right )= \frac{a\left ( a+1 \right )\left ( a+2 \right )\cdots \left ( a+k-1 \right )}{\left ( a+b \right )\left ( a+b+1 \right )\cdots \left ( a+b+k-1 \right )}$
Beta变量$X$的期望和方差分别为:
$E\left ( X \right )= \frac{a}{a+b}$
$Var\left ( X \right )=\frac{ab}{\left ( a+b \right )^{2}\left ( a+b+1 \right )}$
F分布
设$u\sim \chi^{2}\left ( n \right )$,$v\sim \chi^{2}\left ( m \right )$,$u,v$相互独立,$Y= \frac{\frac{u}{n}}{\frac{v}{m}}$的分布称为自由度为$\left ( n,m \right )$的$F$分布,记为:$Y\sim F\left ( n,m \right )$。
性质:$F\left ( n,m \right )= \frac{1}{F\left ( m,n \right )}$。
正态总体的样本均值和样本方差的方差
设$X_{1},X_{2},\cdots ,X_{n}$是取自$N\left ( \mu ,\sigma \right )$的样本,有:$\frac{X_{i}-\mu }{\sigma }\sim N\left ( 0,1 \right ),i=1,2,\cdots ,n$。
结论一:
由卡方分布的定义知:$\frac{\left (X_{i}-\mu \right )^{2} }{\sigma^{2} }\sim \chi^{2}\left ( n \right )$。
结论二:
由假设知:$\sum_{i=1}^{n}X_{i}\sim N\left ( n\mu ,n\sigma ^{2} \right )$,$\frac{1}{n}\sum_{i=1}^{n}X_{i}\sim N\left ( \mu ,\frac{\sigma ^{2}}{n} \right )$,$s^{2}= \frac{1}{n-1}\sum_{i=1}^{n}\left ( X_{i}-\bar{X} \right )^{2}$。
------------------------------------------------------------------------------------------------------------
结论:$\frac{\left ( n-1 \right )s^{2}}{\sigma^{2}}= \frac{\sum_{i=1}^{n}\left ( X_{i}-\bar{X} \right )^{2}}{\sigma^{2}}\sim \chi ^{2}\left ( n-1 \right )$。
$s^{2}$与$\bar{X}$相互独立。
------------------------------------------------------------------------------------------------------------
证明:
令$Z_{i}= \frac{X_{i}-\mu}{\sigma },\quad i=1,2,\cdots ,n$,独立同分布,都服从标准正态分布:$N\left ( 0,1 \right )$;期望为:$\bar{Z}= \frac{1}{n}\sum_{i=1}^{n}Z_{i}= \frac{\bar{X}-\mu }{\sigma }$。则有:
$\frac{\left (n-1 \right )s^{2}}{\sigma ^{2}}= \frac{\sum_{i=1}^{n}\left (X_{i}-\bar{X} \right )^{2}}{\sigma ^{2}}\\ \qquad = \sum_{i=1}^{n} \left [\frac{\left ( X_{i}-\mu \right )-\left ( \bar{X}-\mu \right )}{\sigma } \right ]^{2}\\ \qquad = \sum_{i=1}^{n}\left ( Z_{i}-\bar{Z} \right )^{2} \\ \qquad = \sum_{i=1}^{n}Z_{i}^{2}-n\bar{Z}^{2}$
将$Z_{i},i=1,\cdots ,n$看作 一组空间中的正交基,此时其平方和应该服从自由度为n的卡方分布。但是$\frac{\left (n-1 \right )s^{2}}{\sigma ^{2}}$,还有一项$n\bar{Z}^{2}$,这怎么办呢?解决办法是用正交变化将这项放缩到基向量上,假设这一项映射到$Y_{1}$上,根据高等代数的知识有:$\sum_{i=1}^{n}Z_{i}^{2}=\sum_{i=1}^{n}Y_{i}^{2}$,所以我们希望$Y_{1}^{2}=n\bar{Z}^{2}$。因此设置正交矩阵$A= \left ( a_{ij} \right )$,第一行元素为:$\frac{1}{\sqrt{n}}$,对原始正交基做正交变换得到新的正交基:
$Y= AZ$,其中$Y= \begin{pmatrix} Y_{1}\\ Y_{2}\\ \cdots \\ Y_{n} \end{pmatrix}$,$Z= \begin{pmatrix} Z_{1}\\ Z_{2}\\ \cdots \\ Z_{n} \end{pmatrix}$。
现在我们来证明经过正交变换的新基是相互独立且服从标准正态分布的。
首先,由于$Y_{i}= \sum_{j=1}^{n}a_{ij}Z_{j},i=1,2,\cdots ,n$,所以$Y_{1},Y_{2},\cdots ,Y_{n}$任然是正态随机变量,因为标准正态分布的随机变量的线性组合任然是正态分布。即:
$E\left (Y_{i} \right )=E\left ( \sum_{j=1}^{n}a_{ij}Z_{j} \right )=\sum_{j=1}^{n}a_{ij}E\left (Z_{j} \right )=0$
$Cov\left ( Y_{i},Y_{k} \right )= Cov\left ( \sum_{j=1}^{n}a_{ij}Z_{j},\sum_{l=1}^{n}a_{kl}Z_{l} \right ) \\ \qquad = \sum_{j=1}^{n}\sum_{l=1}^{n}a_{ij}a_{kl}Cov\left ( Z_{j},Z_{l} \right ) \\ \qquad = \sum_{j=1}^{n}a_{ij}a_{kj} \\ \qquad = \delta_{ik}$
注意正交矩阵的性质:有若$A= \left [ \vec{a_{1}},\vec{a_{2}},\cdots ,\vec{a_{n}} \right ]^{T}$,则有:
$\vec{a_{i}}\cdot \vec{a_{k}}= \left\{\begin{matrix} 1,\quad if \quad i=k\\ 0, \qquad else \quad \end{matrix}\right.$
所以有:
$Cov\left ( Y_{i},Y_{k} \right )= \left\{\begin{matrix} 1,\quad if \quad i=k\\ 0, \qquad else \quad \end{matrix}\right.$
通过协方差我们可以知道,新的基$Y_{i}$的方差为1,不同基$Y_{i}$, $Y_{k}$之间相互独立,协方差为0。而均值已经证明为0,且变换后是仍然是正态分布,所以$Y_{i}\sim N\left ( 0,1 \right )$,即仍然是标准正态分布。那么有:
$\frac{\left (n-1 \right )s^{2}}{\sigma ^{2}}=\sum_{i=1}^{n}Z_{i}^{2}-n\bar{Z}^{2}\\ \qquad = \sum_{i=1}^{n}Y_{i}^{2}-Y_{1}^{2}\\ \qquad = \sum_{i=2}^{n}Y_{i}^{2}$
因为$Y_{i}\sim N\left ( 0,1 \right )$,所以有:
$\frac{\left (n-1 \right )s^{2}}{\sigma ^{2}}\sim \chi ^{2}\left ( n-1 \right )$
$s^{2}$与$\bar{X}$相互独立的证明。$\bar{X}= \sigma \bar{Z}+\mu = \frac{\sigma Y_{1}}{\sqrt{n}}+\mu$,而$s^{2}= \frac{\sigma ^{2}}{n-1}\sum_{i=2}^{n}Y_{i}^{2}$,即样本均值只与$Y_{1}$有关,而方差与$Y_{2}, \cdots ,Y_{n}$有关,所以两者之间相互独立。
证毕。
结论三:
结论:$\frac{\bar{X}-\mu}{\frac{s}{\sqrt{n}}}\sim t\left ( n-1 \right )$。
证明:
由$s^{2}= \frac{\sigma ^{2}}{n-1}\sum_{i=2}^{n}Y_{i}^{2}$有:$s= \sigma \sqrt{\frac{\sum_{i=2}^{n}Y_{i}}{n-1}}$。因此有:
$\frac{\bar{X}-\mu}{\frac{s}{\sqrt{n}}} = \frac{\sqrt{n}\left ( \bar{X}-\mu \right )}{\sigma \sqrt{\frac{\sum_{i=2}^{n}Y_{i}}{n-1}}}\\ \qquad = \frac{\frac{\sqrt{n}\left ( \bar{X}-\mu \right )}{\sigma }}{ \sqrt{\frac{\sum_{i=2}^{n}Y_{i}}{n-1}}}$
而:$\frac{\sqrt{n}\left ( \bar{X}-\mu \right )}{\sigma }= Y_{1}\sim N\left ( 0,1 \right )$,$\sum_{i=2}^{n}Y_{i}^{2}\sim \chi^{2}\left ( n-1 \right )$。所以由t分布的定义(正态分布除以根号下卡方分布除以它的自由;卡方分布的自由度就是t分布的自由度)知:
$\frac{\bar{X}-\mu}{\frac{s}{\sqrt{n}}}\sim t\left ( n-1 \right )$
证毕。
Z分布族
Z分布又称 Fisher Z 分布,记为:$Z\left ( a,b \right )$。概率密度函数为:
$p\left ( x;a,b \right )= \frac{\Gamma \left ( a+b \right )}{\Gamma \left ( a \right )\Gamma \left ( b \right )}\frac{x^{a-1}}{\left ( 1+x \right )^{a+b}}$
Z分布的概率密度曲线为:

Z分布的$k$阶矩为:
$E\left ( X^{k} \right )=\frac{\left ( a+k-1 \right ) \left ( a+k-2 \right )\cdots a}{\left ( b-1 \right )\left ( b-2 \right )\cdots \left ( b-k \right )},k< b$
期望和方差分别为:
$E\left ( X \right )=\frac{a}{b-1},b> 1$
$Var\left ( X \right )= \frac{a\left ( a+b-1 \right )}{\left ( b-1 \right )^{2} \left ( b-2 \right )},b> 2$
Z分布与Beta分布之间的关系:
若:$X\sim Be\left ( a,b \right )$,则$Y= \frac{X}{1-X}\sim Z\left ( a,b \right )$。
若:$X\sim Z\left ( a,b \right )$,则$Y= \frac{X}{1+X}\sim Be\left ( a,b \right )$。
Z分布与F分布之间的关系:
若$X\sim Z\left ( \frac{n_{1}}{2},\frac{n_{2}}{2} \right )$,则容易导出$Y= \left ( \frac{n_{2}}{n_{1}} \right )X$的概率密度函数为:
$p\left ( y;n_{1},n_{2} \right )= \frac{\Gamma \left ( \frac{n_{1}+n_{2}}{2} \right )}{\Gamma \left ( \frac{n_{1}}{2} \right )\Gamma \left ( \frac{n_{2}}{2} \right )} \left ( \frac{n_{1}}{n_{2}} \right )^{\frac{n_{1}}{2}} \frac{y^{\frac{n_{1}}{2}-1}}{\left ( 1+\frac{n_{1}}{n_{2}}y \right )^{\frac{n_{1}+n_{2}}{2}}}, y> 0$
这就是自由度为$n_{1}$和$n_{2}$的$F$分布,记为:$F\left ( n_{1},n_{2} \right )$。$F$分布的期望和方差分别为:
$E\left ( Y \right )= \frac{n_{2}}{n_{2}-2},n_{2}> 2$
$Var\left ( Y \right )= \frac{2n_{2}^{2}\left ( n_{1}+n_{2}-2 \right )}{n_{1}\left ( n_{2}-2 \right )^{2}\left ( n_{2}-4 \right )},n_{2}> 4$
学生氏分布------t分布族
若随机变量$X\sim N\left ( 0,1 \right )$与$Y\sim \chi _{n}^{2}$相互独立,则称$T= \frac{X}{\sqrt{\frac{Y}{n}}}$服从自由度为n的$t$分布,记为:$T\sim t_{n}$。它的分布曲线和正态分布类似。概率密度函数为:
$p\left ( x;\alpha \right )= \frac{\Gamma \left ( \frac{\alpha +1}{2} \right )}{\sqrt{\alpha \pi }\Gamma \left ( \frac{\alpha }{2} \right )}\left ( 1+\frac{x^{2}}{\alpha } \right )^{-\frac{\alpha +1}{2}}$
柯西分布
自由度为1的$t$分布就是柯西分布,它以期望和方差都不存在而著名。其概率密度函数为:
$p\left ( x \right )= \frac{1}{\pi \left ( 1+x^{2} \right )},x\in R$
更一般的形式为:
$p\left ( x \right )= \frac{b}{\pi \left ( b^{2}+\left (x-a \right )^{2} \right )},x\in R$
估计量的评价指标
MSE均方误差
公式:$MSE_{\theta }\left ( \hat{\theta} \right )= E\left ( \hat{\theta}-\theta \right )^{2}$。
无偏估计、渐近无偏估计
参数真值是确定的,但是我们未知。则称估计为无偏估计,若$E\left [ \hat{\theta}\left ( X_{1},\cdots ,X_{n} \right ) -\theta \right ]= 0$。估计为渐近无偏估计,若$\lim_{n \to \infty }E_{\theta }\left [ \hat{\theta}\left ( X_{1},\cdots ,X_{n} \right ) \right ]= \theta$。
相合性估计
弱相合性:若$\hat{\theta}\left ( X_{1},\cdots ,X_{n} \right )\xrightarrow[n \to \infty ]{P}\theta $则称$\hat{\theta}\left ( X_{1},\cdots ,X_{n} \right )$作为$\theta $的估计量,具有弱相合性。
强相合性:若$\hat{\theta}\left ( X_{1},\cdots ,X_{n} \right )\xrightarrow[n \to \infty ]{a.s.}\theta $则称$\hat{\theta}\left ( X_{1},\cdots ,X_{n} \right )$作为$\theta $的估计量,具有强相合性。其中$a.s.$表示依概率1收敛or几乎必然收敛。
渐近正态估计
若,$\frac{\hat{\theta}\left ( X_{1},\cdots ,X_{n} \right ) -\theta}{\sigma _{n}\left ( \theta \right )}\xrightarrow[n \to \infty ]{L}N\left ( 0,1 \right )$,其中$\sigma _{n}\left ( \theta \right )$为渐近方差。
假设检验
基本概念
记$H_{0}:\theta \in \Theta_{0}$为原假设;$H_{1}:\theta \in \Theta_{1}$为备择假设。为了对$H_{0}$的正确性做出判断,需要构造一个检验统计量$T\left ( X_{1},X_{2},\cdots ,X_{n} \right )$。当参数$\theta$给定时,检验统计量的分布也能相应确定,样本的取值大小与原假设是否成立有密切联系。假设检验中有一个重要的概念为:接受域、拒绝域。用$W$表示拒绝域,即$W= \left \{ x_{1},x_{2},\cdots ,x_{n}|T\left ( x_{1},x_{2},\cdots ,x_{n} \right )\in G \right \}$,$G$表示检验统计量在原假设下不合理的取值范围。
则有:若$\left ( x_{1},x_{2},\cdots ,x_{n} \right )\in W$则拒绝原假设$H_{0}$,反之接受。原假设是否成立我们是不知道的,但是我们可以根据样本判断其是否落入拒绝域,因此检验规则就是落入就拒绝,不落入就接受,此时就会出现下面的Bug。
第一类错误、第二类错误
第一类错误(拒真):在原假设$H_{0}$成立时,$\left ( x_{1},x_{2},\cdots ,x_{n} \right )$一般不会落入$W$,但由于样本的随机性,也有可能落入$W$。此时按规则将做出拒绝$H_{0}$的错误判断,我们称之为第一类错误(拒真)。
第二类错误(采伪):在原假设$H_{0}$不成立时,$\left ( x_{1},x_{2},\cdots ,x_{n} \right )$一般都会落入$W$,但由于样本的随机性,也有可能不落入$W$。此时按规则将做出接受$H_{0}$的错误判断,我们称之为第二类错误(采伪)。
原假设的拒绝域$W$一旦确定,检验规则也就随之确定了,由于样本的随机性,这两类错误率无法彻底避免。
纽曼皮尔逊(Neyman—Pearson)显著性假设检验原则
优先保证犯第一类错误的概率$\alpha \left ( \theta \right )= P_{H_{0}成立}\left ( 拒绝H_{0} \right )$不超过预先设定的显著性水平(常取0.1、0.05、0.01),在此前提下,使犯第二类错误的概率$\beta \left ( \theta \right )= P_{H_{0}不成立}\left ( 接受H_{0} \right )$尽可能小。
假设检验的势函数
定义势函数为:$g\left ( \theta \right )= P_{\theta }\left \{ \left ( X_{1},X_{2},\cdots ,X_{n} \right )\in W \right \}$。
显然,当$\theta \in \Theta_{0}$时,则$\alpha \left ( \theta \right )= g\left ( \theta \right )$就是犯第一类错误的概率;
当$\theta \in \Theta_{1}$时,有$P_{\theta }\left \{ \left ( X_{1},X_{2},\cdots ,X_{n} \right )\notin W \right \}= 1-P_{\theta }\left \{ \left ( X_{1},X_{2},\cdots ,X_{n} \right )\in W \right \}$,即$\beta \left ( \theta \right )=1- g\left ( \theta \right )$为犯第二类错误的概率。
所以,在$Theta_{0}$中我们希望势函数越小越好,在$Theta_{1}$上希望势函数越大越好。
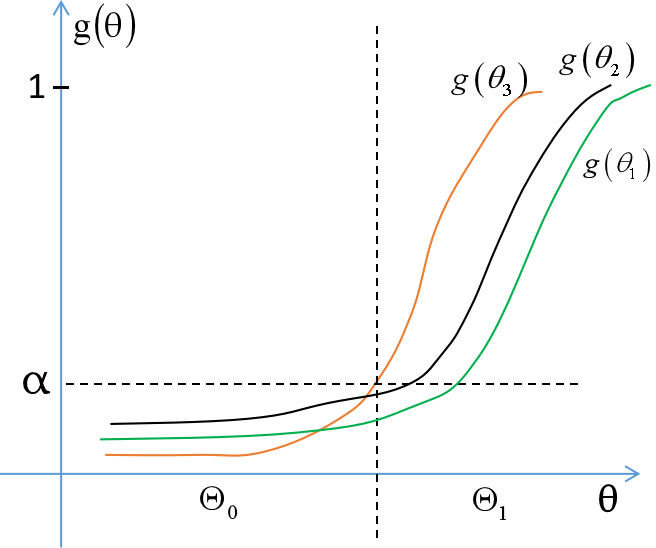
如图所示,第三个势函数要比第一个、第二个势函数好。实际上,我们希望在$Theta_{0}$中,势函数尽可能小,但是在边界点上可以达到$\alpha$,在$Theta_{1}$中,要尽可能大。
当参数$theta$对应的分布是离散型时,势函数$g\left ( \theta \right )$在$Theta_{0}$上的最大值正好等于$\alpha$可能是办不到的,为此引入“随机化检验”,先引入“检验函数”的概念。
非随机化检验函数:将原假设的拒绝域的示性函数:
$\phi \left ( x_{1},x_{2},\cdots ,x_{n} \right ) = \left\{\begin{matrix} 1,\quad if\quad \left ( x_{1},x_{2},\cdots ,x_{n} \right )\in W\\ 0,\quad if\quad \left ( x_{1},x_{2},\cdots ,x_{n} \right )\notin W \end{matrix}\right.$
称为非随机化检验函数。
随机化检验函数:在接受域与拒绝域的边界以概率$r$拒绝原假设,以概率$1-r$接受原假设。随机化检验函数为:
$\phi \left ( x_{1},x_{2},\cdots ,x_{n} \right ) = \left\{\begin{matrix} 1,\quad if\quad \left ( x_{1},x_{2},\cdots ,x_{n} \right )\in W\\ 0,\quad if\quad \left ( x_{1},x_{2},\cdots ,x_{n} \right )\notin W \\ r,\quad if\quad \left ( x_{1},x_{2},\cdots ,x_{n} \right )\in W的边界 \end{matrix}\right.$
纽曼-皮尔逊(Neyman-Pearson)基本引理
如果$\phi_{1}\left ( \vec{X} \right ),\phi_{2}\left ( \vec{X} \right )$是显著性水平$\alpha$的两个检验函数,即$E_{\theta_{0}}\left [ \phi_{1}\left ( \vec{X} \right ) \right ]\leq \alpha$,$E_{\theta_{0}}\left [ \phi_{2}\left ( \vec{X} \right ) \right ]\leq \alpha $,若有$E_{\theta_{1}}\left [ \phi_{1}\left ( \vec{X} \right ) \right ]\geq E_{\theta_{1}}\left [ \phi_{2}\left ( \vec{X} \right ) \right ]$,则称$\phi_{1}\left ( \vec{X} \right )$不比$\phi_{2}\left ( \vec{X} \right )$差。
如果$\phi_{1} \left ( \vec{X} \right )$是显著性水平为$\alpha$下的任意检验函数,如果有$E_{\theta_{1}}\left [ \phi \left ( \vec{X} \right ) \right ]\geq E_{\theta_{1}}\left [ \phi_{1}\left ( \vec{X} \right ) \right ]$,则称$\phi \left ( \vec{X} \right )$是此假设检验的最优势检验(MPT)。
Neyman-Pearson基本引理:若$P_{\Theta_{0}},P_{\Theta_{1}}$是两个不同的概率测度,原假设的MPT一定存在,且可以由似然比给出如下:
$\phi \left ( \vec{X} \right )= \left\{\begin{matrix} 1,\quad P\left ( \vec{X};\theta_{1} \right )> k\cdot P\left ( \vec{X};\theta_{0} \right )\\ 0,\quad P\left ( \vec{X};\theta_{1} \right )< k\cdot P\left ( \vec{X};\theta_{0} \right )\\ r,\quad P\left ( \vec{X};\theta_{1} \right )= k\cdot P\left ( \vec{X};\theta_{0} \right ) \end{matrix}\right.$
由此定理得到就是最优势函数(MPT)。
额,什么?你感觉势函数和检验函数差不多?嗯,实际上确实是,势函数是介绍的连续随机变量分布的情况,主要是用于枢轴量分布的选择,使得第一类错误率不超过显著性水平的情况下,犯第二类错误的概率尽可能小。而检验函数有点类似于离散版的势函数。那么上面的公式用图表示出来是什么样呢?如下图所示:
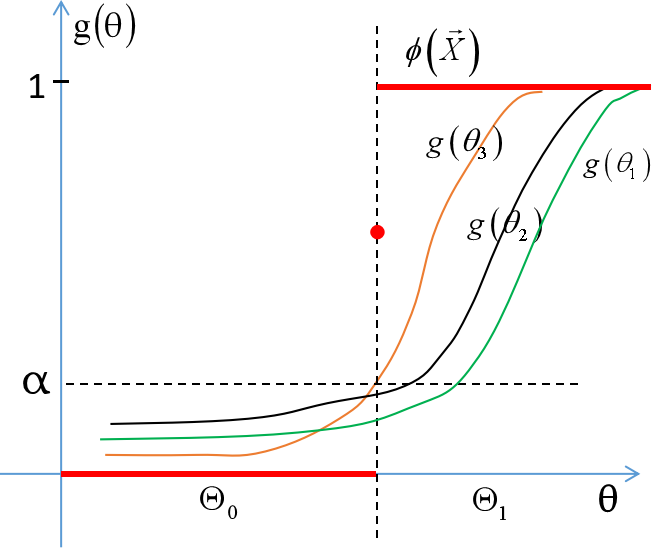
红色的阶梯线表示离散的检验函数,这里将$\vec{X},\theta,W$对应起来了,若$\vec{X}\in W\rightarrow \vec{X}\in \Theta_{1}$;$\vec{X}\notin W\rightarrow \vec{X}\in \Theta_{0}$。不难发现这个极致的情况是真的极端,就因为是离散函数就可以这么吊吗?当然这里属于拒绝域时,检验函数值必须为1,不属于必须为0,边界上的值可以变动,$k$和$r$由$E_{\theta _{0}}\left ( \phi \left ( \vec{X} \right ) \right )= \alpha $来确定。
一致最优势检验
定义:设$\phi \left ( \vec{X} \right )$是显著性水平为$\alpha$的检验,如果对任意一个水平为$\alpha$的检验$\phi_{1} \left ( \vec{X} \right )$,都有:
$E_{\theta}\left [ \phi \left ( \vec{X} \right ) \right ]\geq E_{\theta}\left [ \phi_{1}\left ( \vec{X} \right ) \right ],\forall \theta \in \Theta_{1}$
则,称$\phi \left ( \vec{X} \right )$水平为$\alpha$的一致最优势检验(UMPT)。
此时,你是不是想问MPT与UMPT的定义公式一模一样啊?两者之间有什么区别?MPT是指假设检验为“$H_{0}:\theta= \theta_{0};\quad H_{1}:\theta= \theta_{1}$”这种简单假设的最优势检验,而UMPT是指假设检验为“$H_{0}:\theta= \Theta_{0};\quad H_{1}:\theta= \Theta_{1}$”这种复合假设检验的一致最优势检验,差别就在原假设、备择假设是否有多个选择。
定理一:设$\phi \left ( \vec{X} \right )$是$\left ( \alpha,\Theta_{0},\Theta_{1} \right)$检验,$\Theta_{01}$是$\Theta_{0}$的子集。如果$\phi \left ( \vec{X} \right )$是$\left ( \alpha,\Theta_{01},\Theta_{1} \right)$的UMPT,则$\phi \left ( \vec{X} \right )$是$\left ( \alpha,\Theta_{0},\Theta_{1} \right)$的UMPT。
这里不做证明,原因很简单,接受域中的子集$\Theta_{01}$与完整的拒绝域$\Theta_{1}$结合的UMPT,那么在$\Theta_{0}$和$\Theta_{1}$上也是UMPT,因为我们的条件是在$\Theta_{1}$啊!由$\phi \left ( \vec{X} \right )$是$\left ( \alpha,\Theta_{0},\Theta_{1} \right)$检验有:$E_{\theta _{0}}\left ( \phi \left ( \vec{X} \right ) \right )\leq \alpha,\theta \in \Theta_{0}$。所以条件都是满足的。
定理二:假如对某个$\theta_{0} \in \Theta_{0}$和对每一个$\theta_{1} \in \Theta_{1}$,$\phi \left ( \vec{X} \right )$都是的MPT,则$\phi \left ( \vec{X} \right )$也是$\left ( \alpha,\Theta_{0},\Theta_{1} \right)$的UMPT。
根据定理一及UMPT的定义不难证明其正确性。
未完待续,转载请注明出处……




 浙公网安备 33010602011771号
浙公网安备 33010602011771号