机器学习——正规方程，正则化

一、正规方程（Normal equation）：

对于某些线性回归问题，正规方程方法很好解决；

\(\frac{\partial}{\partial\theta_j}J(\theta_j)=0\),假设我们的训练集特征矩阵为 X(包含了 x0)并且我们的训练集结果为向量 y，则利用正规方程解出向量 \(\theta=(X^TX)^{-1}X^Ty\)

注意：\((X^TX)^{-1}\) 如果特征数量n较大，运算代价就很大，一般小于10000即可；只适用于线性模型；

二、正则化：

解决过拟合问题：

1.丢弃一些不能帮助我们正确预测的特征。可以是手工选择保留哪些特征，或者使用一些模型选择的算法来帮忙（例如PCA）

2.正则化。 保留所有的特征，但是减少参数的大小（magnitude）。

如果我们的模型是：\(h_\theta(x)=\theta_0x_0^0+\theta_1x_1^1+...+\theta_nx_n^n\)

正是这些高次项导致了过拟合的产生，所以去减小他们系数的大小就好了。修改代价函数，给他们的系数设置惩罚；

修改后的代价函数：\(J(\theta)=\frac{1}{2m}[\sum_{i=1}^m(h_\theta(x^{(i)}）-y^{(i)})^2+\lambda\sum_{j=1}^n\theta_j^2]\)

其中\(\lambda\)称作正则化参数，需要对哪个参数惩罚，就把他们加进去，默认全加上。

因为如果我们令\(\lambda\)的值很大的话，为了使Cost Function 尽可能的小，\(\theta_j\)的值都会在一定程度上减小 。。。

（备注： \(\theta_0\)不参与其中的任何一个正则化 ）

2.1正则线性回归的代价函数为：

\(J(\theta)=\frac{1}{2m}\sum_{i=1}^m[((h_\theta(x^{(i)}-y^{(i)})^2+\lambda\sum_{j=1}^n\theta_j^2)]\)

求得更新式子为：\(\theta_j:=\theta_j(1-a\frac{\lambda}{m})-a\frac{1}{m}\sum_{i=1}^m(h_\theta(x^{(i)})-y^{(i)})x_j^{(i)}\) 可以看出，正则化线性回归的梯度下降算法的变化在于，每次都在原有算法更新规则的基础上令 \(\theta\)值减少了一个额外的值。

若用正规方程求解：

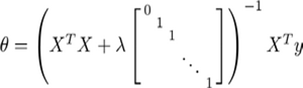
2.2正则逻辑回归的代价函数为：

\(J(\theta)=\frac{1}{m}\sum_{i=1}^m[-y^{(i)}log(h_\theta(x^{(i)}))-(1-y^{(i)})log(1-h_\theta(x^{(i)}))]+\frac{\lambda}{2m}\sum_{j=1}^n\theta_j^2\)

梯度更新式子和正则线性的一样的注：看上去同线性回归一样，但是知道 \(h_\theta(x)=g(\theta^TX)\) ，所以与线性回归不同。