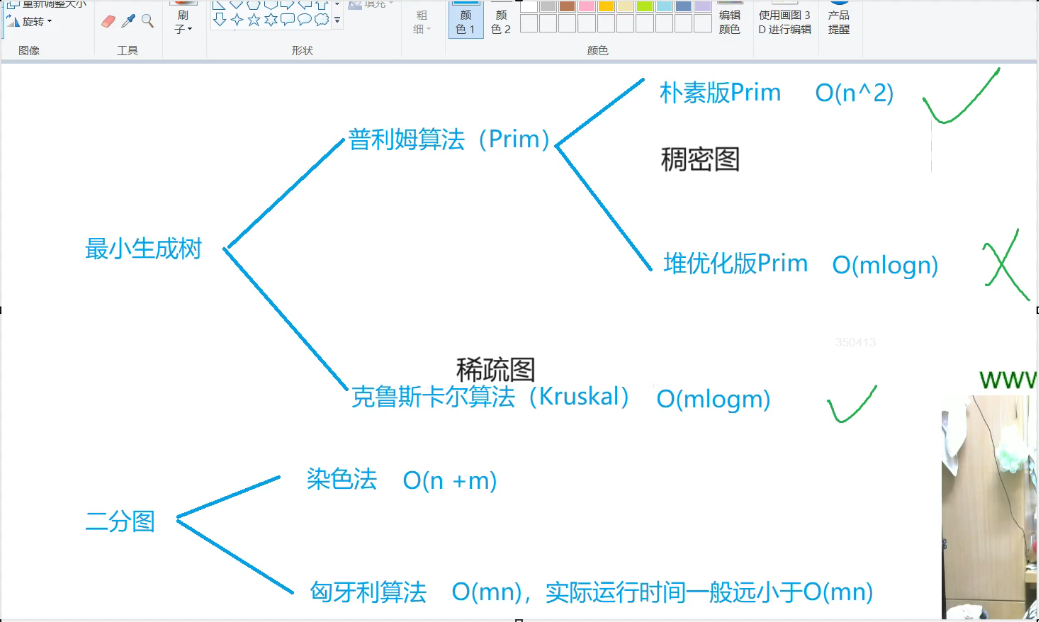
最小生成树、二分图(11/2)

到集合得最短距离是指点到集合中的所有点最短距离，集合就是遍历或正选中的数

prim

#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
int n,m;
const int N=510 ;const int INF=0x3f3f3f3f;
int g[N][N];
int dist[N];
bool st[N];

int prim()
{
    memset(dist,0x3f,sizeof dist);
    int res=0;
    for(int i=0;i<n;i++)
    {
        //找到最近的点，t=-1的话直接更新
        int t=-1;
        for(int j=1;j<=n;j++)
          if(!st[j]&&(t==-1||dist[j]<dist[t]))
            t=j;
        
        if(i && dist[t]==INF) return INF;//首先判断，如果距离为无穷就是没有最小生成树，不连通
        
        if(i) res+=dist[t];//注意i=0的时候，dist为无穷，不算入，从第二个点加，第一个点加也没意义
        
        st[t]=true;//标记
        
    for(int j=1;j<=n;j++) dist[j]=min(dist[j],g[t][j]); //注意此处更新的是距离集合最近的点
    }
    return res;
}

int main()
{
    memset(g,INF,sizeof g);
    scanf("%d%d",&n,&m);
    while(m--)
    {
        int a,b,c;
        scanf("%d%d%d",&a,&b,&c);
        g[a][b]=g[b][a]=min(g[a][b],c);
    }
    
    int t=prim();
    if(t==INF) puts("impossible");
    else 
    printf("%d",t);
    return 0;
}