最短路（10/25）

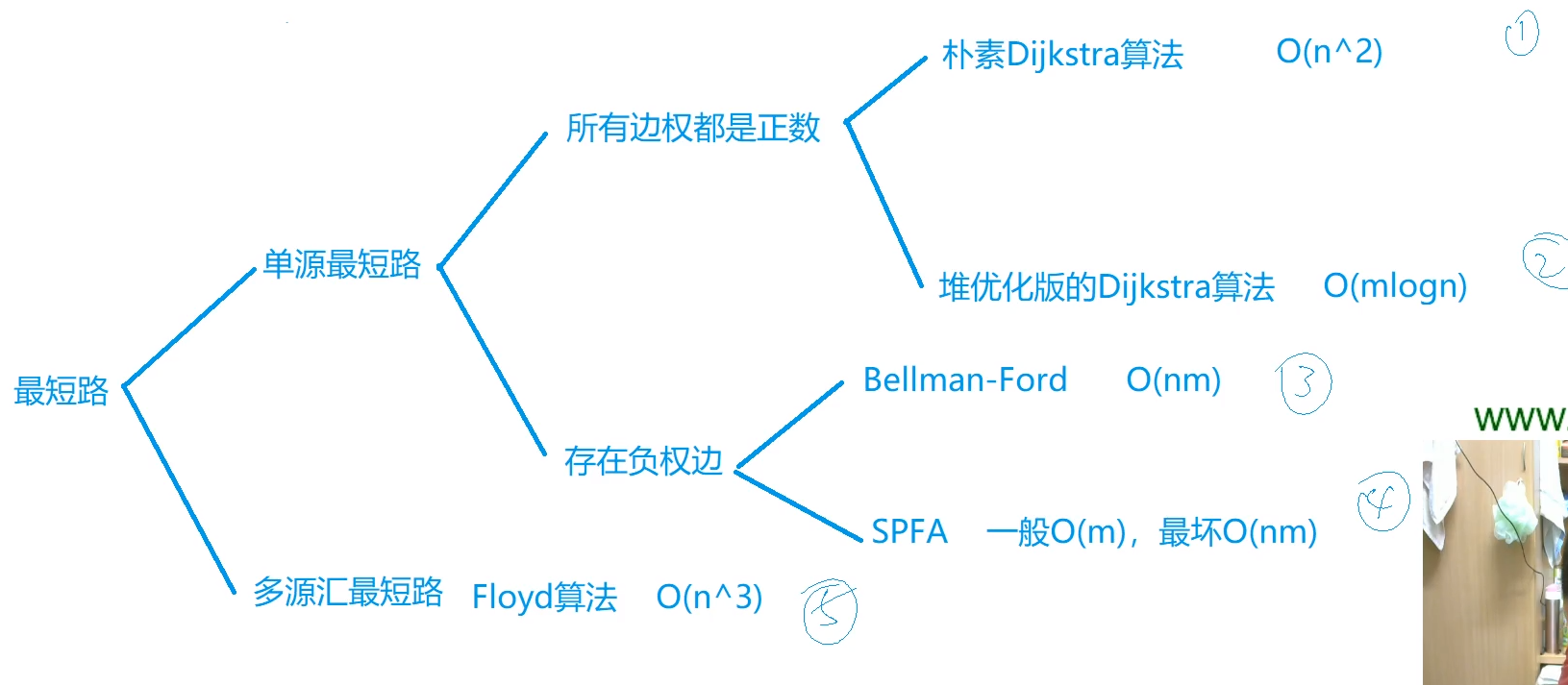
n是点数   m是边数

退优化版的适合点数和边数差不多

（3）适合对边有限制

稠密图用邻接矩阵存

稀疏图用邻接表来存

朴素dijkstra

#include<cstring>
#include<iostream>
using namespace std;
int n,m;
const int N=510;
int g[N][N];//记录点之间的权值
int dist[N];//记录点到原点的最短距离
bool st[N];//距离是否已经走过
int dijkstra()
{
    memset(dist ,0x3f,sizeof dist);//赋值成无穷
    dist[1]=0;//从第一个点开始
    for(int i=0;i<n;i++)
    {
        int t=-1;
        for(int j=1;j<=n;j++)//遍历每个没走过点，找到最近的一个点
            if(!st[j]&&(t==-1||dist[j]<dist[t]))
            t=j;
        st[t]=true;//将该点记录
        for(int j=1;j<=n;j++)//更新所有点的距离
        dist[j]=min(dist[j],dist[t]+g[t][j]);
    }
    if(dist[n]==0x3f3f3f3f) return -1;//0x3f3f3f3f再多就超过32位，溢出导致错误
    else
    return dist[n];
}

int main()
{
    memset(g,0x3f,sizeof g);
    scanf("%d%d",&n,&m);
    int x,y,z;//左点  右点 权值
    while(m--){
       scanf("%d%d%d",&x,&y,&z);
       g[x][y]=min(g[x][y],z);
    }
    printf("%d\n",dijkstra());
    return 0;
}

堆优化版本

priority_queue<PII,vector<PII>,greater<PII>>heap，小分堆定义
引入头文件queue

#include<cstring>
#include<iostream>
#include<algorithm>
#include<queue>
using namespace std;
typedef pair<int,int>PII;
int n,m;
const int N=1000010;
int h[N],e[N],ne[N],k[N],idx=0;
int dist[N];//记录点到原点的最短距离
bool st[N];//距离是否已经走过

void add(int a,int b,int c){
    e[idx]=b;k[idx]=c;ne[idx]=h[a];h[a]=idx++;    
}


int dijkstra()
{
    priority_queue<PII,vector<PII>,greater<PII>>heap;//小分堆，最小值自动在最上面
    memset(dist ,0x3f,sizeof dist);//赋值成无穷
    dist[1]=0;//从第一个点开始
    heap.push({0,1});//放第一个值
    while(heap.size())
    {
        auto t=heap.top();
        heap.pop();
        int ver=t.second;int distance=t.first;
        if(st[ver]) continue;//如果遍历过就继续
        st[ver]=true;
        for(int i=h[ver];i!=-1;i=ne[i])//遍历相邻节点，类似广搜
        {
            int j=e[i];
            if(dist[j]>dist[ver]+k[i])//起点加权值如果小于原来大小就更新距离，并加入堆中
            {
                dist[j]=dist[ver]+k[i];
                heap.push({dist[j],j});
            }
        }
    }
    if(dist[n]==0x3f3f3f3f) return -1;//0x3f3f3f3f再多就超过32位，溢出导致错误
    return dist[n];
}

int main()
{
    memset(h,-1,sizeof h);
    scanf("%d%d",&n,&m);
    int x,y,z;//左点  右点 权值
    while(m--){
       scanf("%d%d%d",&x,&y,&z);
       add(x,y,z);
    }
    printf("%d\n",dijkstra());
    return 0;
}