解“过河卒”编程题的收获———第一次随笔

棋盘上 AA 点有一个过河卒，需要走到目标 BB 点。卒行走的规则：可以向下、或者向右。同时在棋盘上 CC 点有一个对方的马，该马所在的点和所有跳跃一步可达的点称为对方马的控制点。因此称之为“马拦过河卒”。

棋盘用坐标表示，AA 点 (0, 0)(0,0)、BB 点 (n, m)(n,m)，同样马的位置坐标是需要给出的。

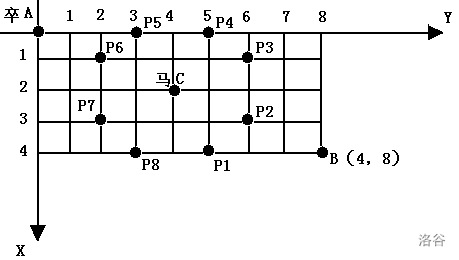
现在要求你计算出卒从 AA 点能够到达 BB 点的路径的条数，假设马的位置是固定不动的，并不是卒走一步马走一步。

输入格式

一行四个正整数，分别表示 BB 点坐标和马的坐标。

输出格式

一个整数，表示所有的路径条数。

输入输出样例

输入 #1复制

6 6 3 3

输出 #1复制

6

说明/提示

对于 100 \%100% 的数据，1 \le n, m \le 201≤n,m≤20，0 \le0≤ 马的坐标 \le 20≤20。

我的解题代码如下：

#include<iostream>
#include<ctime>
#include<cstdlib>
#include<algorithm>
using namespace std;
#define ull unsigned long long
const int fx[] = { -2, -1, 1, 2, 2, 1, -1, -2 };//这两个数组存放的是马的八个控制点，方便主函数里边标记
const int fy[] = { 1, 2, 2, 1, -1, -2, -2, -1 };
int bx, by, cx, cy;//分别定义终点、马的横纵坐标，
ull f[30][30];//记录行走路径，全局整型类变量默认值为0
bool s[30][30];//存放马和马控制点的坐标
int main()
{
　　cin >> bx>>by>>cx>>cy;
　　bx += 2; by += 2; cx += 2; cy += 2;//终点和马同时往右下角移2个位置；防止下面的递归运算开始就越界
　　for (int i = 0; i < 8; i++)
　　{
　　　　s[cx + fx[i]][cy + fy[i]] = 1;//把马的控制点和下行的马标记为1
　　}
　　s[cx][cy] = 1;
　　f[2][2] = 1;//向右下平移了两个位置的初始点赋值为1
　　for (int i = 2; i <=bx; i++)
　　{
　　　　for (int j = 2; j <=by; j++)
　　　　{
　　　　　　if (s[i][j])//遇见马和马的控制点就越过递归，继续循环
　　　　　　continue;
　　　　　　f[i][j] = max(f[i][j], f[i - 1][j] + f[i][j - 1]);//该语句为核心。求到达终点的路径数，就是求到达终点上边和左边路径数之和，以此递推
　　　　}
　　}
　　　　cout << f[bx][by];
　　　　return 0;
}

最后：写这个随笔是为了记录我学习编程的足迹。才开始做编程题，这道题也是我看了大神的题解，然后花了几个小时才弄懂，最后才写出来的。上边的注释是根据我的理解写的，有错误的话欢迎指出。