【bellman-ford】AcWing853.有边数限制的最短路——模板题

AcWing853.有边数限制的最短路

题解

存在负权回路可能会导致无法求最短路，比如说图中 2的自环，没转一圈距离-1，我们求1到5的距离可以转无穷圈2，即1到2的距离为 -无穷

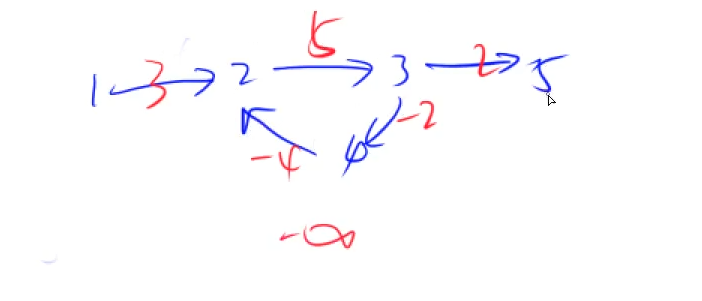
循环n次求的是长度不超过n条边的最短路

#include <iostream>
#include <cstring>
using namespace std;

const int N = 10010, M = 510;

int n, m ,k;
int dist[M], backup[M]; //backup用于备份由于bellaman_ford会改变前面的dist[a]导致结果不对
struct{
    int a, b, w;
}edge[N];

void bellman_ford()
{
    memset(dist, 0x3f3f3f3f, sizeof dist);
    dist[1] = 0;
    for(int i = 0; i < k; ++i)
    {
        memcpy(backup, dist, sizeof dist);
        for(int j = 0; j < m; ++j)
            {
                auto t = edge[j];
                dist[t.b] = min(dist[t.b], backup[t.a] + t.w);
            }
    }
}

int main()
{
    cin >> n >> m >> k;
    int a, b, w;
    for(int i = 0; i < m; ++i)
    {
        cin >> a >> b >> w;
        edge[i] = {a, b, w};
    }
    bellman_ford();
    //负权边可能会导致1到n的不可能路线变小
    if(dist[n] > 0x3f3f3f3f / 2) cout << "impossible" << endl;
    else cout << dist[n] << endl;
    return 0;
}