【数论】Acwing1223.最大比例(更项相减术——辗转相减)

题目

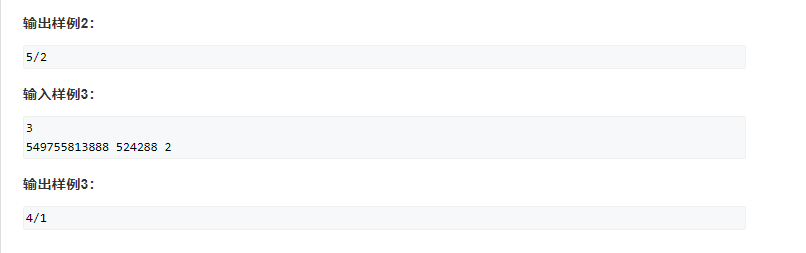
题解

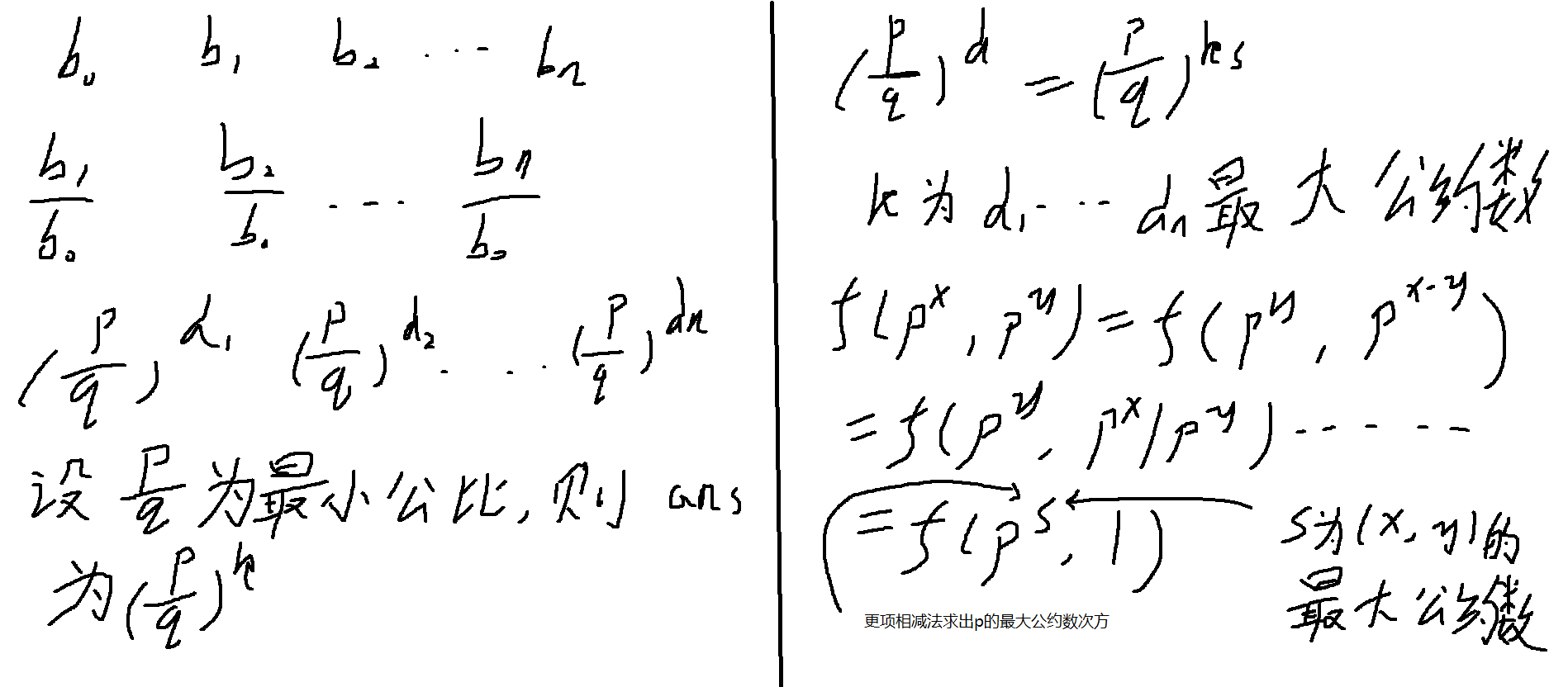
#include <iostream>
#include <algorithm>

using namespace std;
typedef long long LL;
const int N = 110;

int n;
int cnt;
LL a[N],b[N],c[N]; //a为分子 b为分母

LL gcd(LL x, LL y)
{
    return y ? gcd(y, x % y) : x;
}

LL gcd_sub(LL x, LL y)
{
    if(x < y) swap(x,y);
    if(y == 1) return x;
    return gcd_sub(y,x/y);
}

int main()
{
    cin >> n;
    for(int i = 0; i < n; ++i)
        cin >> c[i];
    sort(c,c+n);
    LL d;
    for(int i = 1; i < n; ++i)
        if(c[i] != c[i-1])
        {
            d = gcd(c[i],c[0]);
            a[cnt] = c[i] / d;
            b[cnt++] = c[0] / d;
        }
    LL up = a[0], down = b[0];
    for(int i = 1; i < cnt; ++i)
        {
            up = gcd_sub(up,a[i]);
            down = gcd_sub(down,b[i]);
        }
    cout << up << "/" << down << endl;
    return 0;
}