[总结][数学][笔记]数学专题
数学专题
快速幂
例题
算法用途
快速幂主要用于快速求出形如\(a^b\)的问题,如果是暴力的话要运算\(b\)次,而用快速幂只需计算\(log_2(b)\)次。
算法原理
例如现在要求的是\(3^{12}\),我们把\(12\)用二进制来表示是\(1100\),那么原问题就变成了求\(3^4*3^8\),那么其实就是在\(12\)的二进制表示下为\(1\)的那一位进行运算,原理很简单,不好讲,直接看代码吧
代码实现
int pow(int a,int b){
int res = 1;
while(b){
if(b & 1)
res = res * a;
a *= a;
b >>= 1;
}
}
非常的简洁。
矩阵快速幂
例题
算法介绍
学习矩阵快速幂的一个必要前置知识就是快速幂这不是废话吗,说到底,矩阵快速幂=矩阵乘法+快速幂。
矩阵乘法
现在有两个矩阵\(A,B\),\(A\)的大小是\(n*m\),\(B\)的大小是\(m*k\),注意矩阵乘法的时候两个矩阵一定要有一维的长度是一样的,原因就在与矩阵乘法的原理,原理就是矩阵\(A\)的第\(i\)行乘以矩阵\(B\)的第\(j\)列,得到的值就是新矩阵\(C\)中坐标为\(i\)行\(j\)列的点的值,来看三幅图: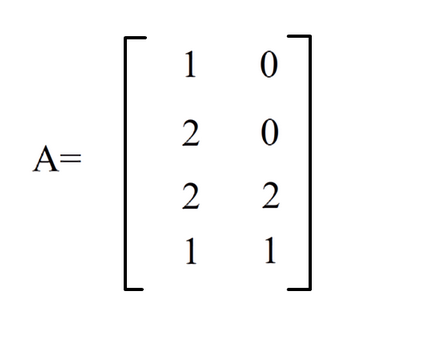
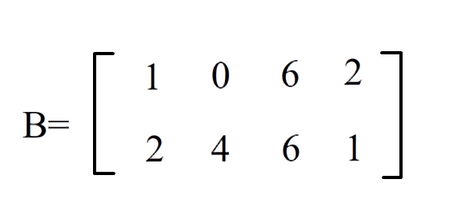
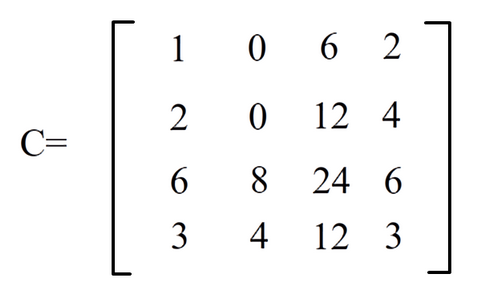
一般来说矩阵乘法对于两个矩阵的先后顺序是有要求的,也就是说两个矩阵不能调换先后顺序。好,对于上图的矩阵\(A,B\),回忆一下矩阵乘法的法则:矩阵\(A\)的第\(i\)行乘以矩阵\(B\)的第\(j\)列变成矩阵\(C\)的第\(i\)行\(j\)列的元素,那么我们取矩阵\(A\)的第\(2\)行,矩阵\(B\)的第\(2\)列,分别是\([2 \ \ 0],[0 \ \ 4]\),进行对位相乘并把所得的积相加:\(2 * 0+0*4=0\),因此矩阵\(C\)中第\(2\)行\(2\)列的元素就是\(0\)。
矩阵快速幂的实现
具体的实现就跟快速幂差不多,就是把快速幂拆分二进制后进行的四则运算的乘法改成了矩阵乘法啦。
#include <bits/stdc++.h>
using namespace std;
struct mat{
long long a[110][110];
};
const int mod = 1e9 + 7;
mat mul(mat a,mat b,long long n){
mat c;
memset(c.a,0,sizeof(c,a));
for(int i = 1;i <= n;i++){
for(int j = 1;j <= n;j++){
for(int k = 1;k <= n;k++){
c.a[i][j] += a.a[i][k] * b.a[k][j];
c.a[i][j] %= mod;
}
}
}
return c;
}
mat pow(mat x,long long n,long long k){
mat res;
for(int i = 1;i <= n;i++)
res.a[i][i] = 1;
while(k){
if(k % 2)
res = mul(res,x,n);
x = mul(x,x,n);
k >>= 1;
}
return res;
}
int main(){
long long n,k;
mat tmp;
cin>>n>>k;
for(int i = 1;i <= n;i++){
for(int j = 1;j <= n;j++){
cin>>tmp.a[i][j];
}
}
mat ans = pow(tmp,n,k);
for(int i = 1;i <= n;i++){
for(int j = 1;j <= n;j++){
cout<<ans.a[i][j]<<' ';
}
cout<<endl;
}
return 0;
}
同余
基本概念
若\(a,b\)两个整数,且它们的差\(a-b\)可以被某个自然数\(m\)整除,那么就说\(a\)就模\(m\)而言同余于\(b\)。简单来说就是\(a\%m=b\%m\),同余表示为\(a\equiv b(mod\ m)\)。(注意取模的模数一定要是自然数,即\(m>0\))
基本性质
1.自反性:\(a\equiv a(mod\ m)\)
2.对称性:若\(a\equiv b(mod\ m)\),则\(b\equiv a(mod\ m)\)
3.传递性:若\(a\equiv b(mod\ m),b\equiv c(mod\ m)\)则有\(a\equiv c(mod\ m)\)
4.同加性:若\(a\equiv b(mod\ m)\)则有\(a+c\equiv b+c(mod\ m)\)
5.同乘性:若\(a\equiv b(mod\ m)\),则\(a*c\equiv b*c(mod\ m)\);若\(a\equiv b(mod\ m),c\equiv d(mod\ m)\),则有\(a*c\equiv b*d(mod\ m)\)
6.同幂性:若\(a\equiv b(mod\ m)\)则有\(a^n\equiv b^n(mod\ m)\)
一个小应用
问题:求解\(m^n\ mod\ k\)的值。
做法:
首先说一个特例情况:求解\(3^{89}\ mod\ 7\)。
这样我们就可以推出一个普遍的解法。对于\(m^n\%k\)的问题,首先把\(n\)拆成二进制,存在一个数组\(a\)里,\(a[i]=1\)表示的就是\(n\)二进制第\(i\)位是\(1\)。然后从小到大逐个求出\(m^i \ mod\ k\)的值。
注意前面讲的很复杂,其实这道例题的本质就是对快速幂进行取模操作,所以实现起来和快速幂没有区别,只是在每个运算后模了一下,可以当作是对快速幂的另一种理解吧,也能增进同余的理解
代码:
#include <bits/stdc++.h>
using namespace std;
int main(){
int n,m,k;
scanf("%d%d%d",&n,&m,&k);
int ans = 1;
while(n){
if(n & 1){
ans *= m;
ans %= k;
}
m *= m;
m %= k;
n >>= 1;
}
printf("%d\n",ans);
return 0;
}
最大公约数-\(GCD\)
辗转相除法
算法原理
辗转相除法也称为欧几里得算法,基本原理就是两个数不断的用较大的数减去较小的数,知道较小的数变成了\(0\),剩下的那个数就是两个数的最大公约数。
举个栗子:我们要求\(gcd(6,20)\rightarrow gcd(6,14)\rightarrow gcd(6,8)\rightarrow gcd(2,6)\rightarrow gcd(2,4)\rightarrow gcd(2,2)\rightarrow gcd(0,2)\)因此\(6\)和\(20\)的最大公约数就是\(2\)。我们观察上面的推导过程,发现进行了很多重复的减法,所以我们可以用取模运算直接得到余数,从而进行优化。
算法实现
int gcd(int x,int y){
if(x == 0)return y;
return gcd(y % x,x);
}
最小公倍数
引理
\(a,b\)两个数的最大公约数乘以它们的最小公倍数就等于\(a,b\)两数的乘积
算法讲解
根据上面的引理我们可以直接根据最大公约数来求出最小公倍数,举个例子:求\(3,8\)的最小公倍数。那么我们就可以列出式子\(lcm(3,8)=(3*8)\div gcd(3,8)=24\div 1=24\)。
扩展欧几里得算法
算法用途
扩展欧几里得算法是用来在已知\((a,b)\)时,求一组解\((p,q)\),使得\(p*a+q*b=gcd(a,b)\)
裴蜀定理
这里需要补充一个定理------裴蜀定理。它是用来证明上面的问题一定有解的。证明过程参考。
一道例题
这道题的解法就是把所有数都先取绝对值,然后答案就是所有数的最大公约数,问什么取绝对值呢?因为反正系数是随便取的所以如果给出的数正负颠倒了,系数相应的变化即可。再来说说为什么答案是所有数的最大公约数。若\(a_1,a_2...a_3\)都是整数,并且\(gcd(a_1,a_2...a_n)=d\),那么对于任意的整数\(x_1a_1,x_2a_2...x_na_n\)都一定是\(d\)的倍数,并且一定存在整数\(x_1,x_2...x_n\)使得\(x_1a_1+x_2a_2+...+x_na_n=d\),这个时候\(x_1,x_2...x_n\)就是我们的最有序列,那么答案就是\(d\)。
代码:
#include <bits/stdc++.h>
using namespace std;
int gcd(int x,int y){
if(x == 0)return y;
return gcd(y % x,x);
}
int main(){
int n,ans;
scanf("%d",&n);
scanf("%d",&ans);
for(int i = 2;i <= n;i++){
int x;
scanf("%d",&x);
x = abs(x);
if(ans > x)ans = gcd(x,ans);
else ans = gcd(ans,x);
}
printf("%d\n",ans);
return 0;
}
求解过程
代码实现
#include <bits/stdc++.h>
using namespace std;
int x,y;
int ex_gcd(int a,int b){
int res,tmp;
if(b == 0){
x = 1,y = 0;
return a;
}
res = ex_gcd(b,a % b);
tmp = x;
x = y;
y = tmp - a / b * y;
return res;
}
int main(){
int a,b;
scanf("%d%d",&a,&b);
ex_gcd(a,b);
printf("%d %d",x,y);
return 0;
}
乘法逆元
既然已经将了扩欧就顺带把逆元也讲了吧
定义
如果在\(mod\ p\)的意义下,一个整数\(a\),有\(a*b\equiv 1(mod\ p)\),那么整数\(b\)就称为\(a\)的乘法逆元,同时\(a\)也称为\(b\)的乘法逆元。要注意的是一个数要有逆元的充要条件为\(gcd(a,p)=1\)
作用
我们知道在进行除法的时候是不能取模的,换句话说就是:\(a\div b\ mod \ p\neq \ (a \ mod \ p \div \ b \ mod \ p) \ mod \ p\)。
同时我们也知道乘法是可以进行取模操作的。所以就来一波转化:
求解
费马小定理
概述
在做形如:\(a\div b \% p\)的题时如果模数\(p\)是质数并且\(b\)不是\(p\)的倍数,则有\(b^{p-2}\equiv 1(mod \ p)\)根据我做过的道题来看,大部分的模数都是质数,所以大部分情况下可以直接得到逆元\(x\equiv b^{p-2}\),为什么是\(x\)和\(b^{p-2}\)同余而不是相等呢?因为逆元可能有很多个,\(x\)和\(b^{p-2}\)意义相同但是数值可能不一样。
代码实现
原题为\(lgP3811\)
#include <iostream>
#include <cstdio>
using namespace std;
long long n,p;
inline long long read(){
long long x = 0,f = 1;
char ch;
ch = getchar();
while(!isdigit(ch)){
if(ch == '-')
f = -1;
ch = getchar();
}
while(isdigit(ch)){
x = x * 10 + ch - '0';
ch = getchar();
}
return x * f;
}
inline long long qpow(long long x,long long y){
long long res = 1;
while(y){
if(y & 1){
res *= x;
res %= p;
}
x *= x;
x %= p;
y >>= 1;
}
return res % p;
}
int main(){
ios::sync_with_stdio(false);
n = read();p = read();
for(register long long i = 1;i <= n;i++){
printf("%lld\n",qpow(i,p - 2) % p);
}
return 0;
}
一种线性做法
大致讲解
上面的代码虽然正确,但是会超时,如果你想过这道题,所以这里讲一个线性的做法。
假设你要求的是\(1\texttt{~}n\)的所有数的逆元,用\(inv[i]\)表示数\(i\)的在模\(P\)意义下的逆元。公式是这样的\(inv[i]=(n-n\div i)*inv[n\%i]\%n\),具体证明过程如下:
附上\(\color{green}{\texttt{AC}}\)代码
#include <bits/stdc++.h>
using namespace std;
long long inv[3000010];
int main(){
int n,p;
scanf("%d%d",&n,&p);
inv[1] = 1;
printf("1\n");
for(int i = 2;i <= n;i++)
inv[i]=p-(p/i)*inv[p%i]%p,printf("%d\n",inv[i]);
return 0;
}
期望
概念
期望在信息学中指的一般是达到结果的期望,最简单的计算方法就是每个情况的概率乘以这个情况的结果的值
例题理解以及公式
问题1
持续地抛一枚硬币,直到连续两次硬币正面朝上,求期望要抛的次数
解答:设\(f_0\)为没有抛出过正面的期望次数,\(f_1\)为已经抛出一次正面还要再抛一个正面的期望次数,则可以得到
问题2
你面前有\(n\)扇门,每道门有一个战力要求\(c_i\)和时间\(t_i\)同时你有一个战斗力\(v\)。每一轮你都会随机挑选一扇门进行挑战:若\(v>c_i\)则会花费\(t_i\)的时间离开;否则战力提升\(c_i\)。求期望多少轮后能离开?\(n ≤ 100, v, c_i ≤ 10^4\)
解答:设\(f_i\)代表战力为\(i\)时期望的逃离时间,则可以知道:
问题3
买彩票。一张彩票\(2\)元,每卖出\(1000000\)张就开奖,中奖号码是\(342356\),每张彩票也是一个\(6\)位数的数字,奖励规则如下:
-
最后一位相等奖励\(4\)元,中奖概率\(0.1\%\)
-
后两位相等奖励\(20\)元,中奖概率\(0.01\%\)
-
后三位相等奖励\(200\)元,中奖概率\(0.001\%\)
-
后四位相等奖励\(2000\)元,中奖概率\(0.0001\%\)
-
后五位相等奖励\(20000\)元,中奖概率\(0.00001\%\)
求彩票公司每卖出一张彩票的期望收益。
解答:通过上面两道比较简单的例题立即期望的概念,我们知道算期望就是把每种情况的权值与它对应的概率相乘。那么来看这道题。先计算公司的期望支出:\(0.1*4+0.01*20+0.001*2000+0.00001*20000=1.2\),也就意味着每卖出一张彩票公司的期望支出为\(1.2\)元,而彩票的单价是\(2\)元,所以公司每卖出一张彩票的期望收益就是\(0.8\)元。
公式
期望用\(E\)表示,概率用\(P\)表示,则有:\(E(x)=X_1*P(X_1)+X_2*P(X_2)+...+X_n*P(X_n)\)
洛谷\(\texttt{P3232}\)题解
有了对期望的大致了解就可以来看洛谷的这道题了。
思路分析
根据贪心的原则,为了使答案尽可能的小,那么期望经过次数多的边的编号就要尽可能的小。那么问题就变成了求每条边的期望经过次数,那么再想一条边被经过肯定是由它的两个端点来的,那么就可以表示一下:\(g_e\)表示经过边\(e\)的期望次数,\(f\)表示点的期望经过次数,\(d\)表示点的入度,就\(g_e=\frac{f_u}{d_u}+\frac{f_v}{d_v}\),因为每次到达一个点\(u\)的时候都有\(\frac{1}{d_u}\)的概率经过边\(e\)。那么问题又转化成求经过点的期望次数:\(f_u=\sum_{v\in E_u}\frac{f_v}{d_v} \ \ {(E_u)表示的是和u相连的点集}\),但要注意\(1\)号节点不一样,\(f_1=1+\sum_{v\in E_u}\frac{f_v}{d_v}\),因为一开始就走过了,而\(n\)号节点是目标节点,走到了就不能再到别的点了所以\(f_n=0\)。
接着就是求解了,我们可以把上面\(f\)的式子看作\(n-1\)个方程,用高斯消元求解就行。但这里既然是用高斯消元求解就要表示成格式统一的方程式,方法如下:
代码
#include <bits/stdc++.h>
using namespace std;
struct node{
int to,nxt;
}e[125010 * 2];
int fir[510],tot,d[510];
int u[125010],v[125010];
void add(int x,int y){
e[++tot].to = y;
e[tot].nxt = fir[x];
d[x]++;
fir[x] = tot;
}
int n,m;
double eps = 1e-9;
double f[510][510],g[125010];
void gauss(){
for(int i = 1;i <= n;i++){
int now = i;
for(int j = i + 1;j <= n;j++){
if(fabs(f[j][i]) > fabs(f[now][i]))
swap(now,j);
}
if(now != i)
for(int j = 1;j <= n + 1;j++)
swap(f[i][j],f[now][j]);
if(fabs(f[i][i]) < eps)continue;
for(int j = 1;j <= n;j++){
if(j != i){
double tmp = f[j][i] / f[i][i];
for(int k = i + 1;k <= n + 1;k++){
f[j][k] -= f[i][k] * tmp;
}
}
}
}
for(int i = 1;i <= n;i++){
f[i][n + 1] /= f[i][i];
}
}
int main(){
scanf("%d%d",&n,&m);
for(int i = 1;i <= m;i++){
scanf("%d%d",&u[i],&v[i]);
add(u[i],v[i]);add(v[i],u[i]);
}
n--;//n号点不能转移
f[1][n + 1] = -1.0;//模拟移项的过程
for(int i = 1;i <= n;i++){
f[i][i] = -1;
for(int j = fir[i];j;j = e[j].nxt){
if(e[j].to != n + 1)
f[i][e[j].to] = 1.0 / d[e[j].to];
}
}
gauss();
for(int i = 1;i <= m;i++){
g[i] = f[u[i]][n + 1] / d[u[i]] + f[v[i]][n + 1] / d[v[i]];
}
sort(g + 1,g + m + 1);
double ans = 0.0;
for(int i = 1;i <= m;i++){
ans += g[i] * (m - i + 1);
}
printf("%.3lf\n",ans);
return 0;
}
组合数学
基本公式
欧拉函数
定义
欧拉函数即\(\phi(n)\),表示的是小于等于\(n\)的数中和\(n\)互质的数的个数----\(\texttt{OIWiki}\)
举个例子\(\phi(1)=1\)。
形式化的表达式:\(\phi(n)=n*(1-\frac{1}{p_1})*(1-\frac{1}{p_2})*...*(1-\frac{1}{p_r}),其中n=p_1^{k_1}*P_2^{k_2}*...*p_r^{k_r},p为质数\)
性质
\(\color{pink}{I}\)
\(如果gcd(a,b)=1,那么\phi(a*b)=\phi(a)*\phi(b),特别地,如果n是奇数,\phi(2*n)=\phi(n),这个成为欧拉函数的积性\)
\(\color{pink}{II}\)
\(n=\sum_{d|n}\phi(d)\)。
证明:设\(f(x)\)表示\(gcd(k,n)=x\)的数的个数,那么\(n=\sum^n_{i=1}f(i)\)。我们发现\(f(x)=\phi(\frac{n}{d})\),所以进一步化简为\(n=\sum_{d|n}\phi(\frac{n}{d})\),同时\(n\)和\(frac{n}{d}\)其实是等价的,只是交换了顺序,所以就得到了原始公式。
\(\color{pink}{III}\)
若\(n=p^k\),\(p\)为质数,那么\(\phi(n)=p^k-p^{k-1}\)
\(\color{pink}{IV}\)
若\(p\)为质数,则\(phi(p)=p - 1\)
求法
如果只要求一个数的欧拉函数值,只要根据定义把这个数进行质因数分解就可以了。
代码
int phi(int n){
int ans = n;
for(int i = 2;i <= n;i++){
if(n % i == 0)
ans -= ans / i;
while(n % i == 0)n /= i;
}
if(n > 1)ans = ans / n * (n - 1);
return ans;
}
未完待续.....


 浙公网安备 33010602011771号
浙公网安备 33010602011771号