[学习笔记] 数学入门
真的只是入门啊,窝只会入门
裴蜀定理
内容
对于任何整数a,b,d关于未知数和的裴蜀等式:a*u+b*v=m,有整数解时当且仅当m是a及b的最大公约数d的倍数。裴蜀等式有解时必然有无穷多个整数解,每组解x、y都称为裴蜀数,可用扩展欧几里得算法求得
简而言之:\(ax + by = c, x \in N^+,y \in N^+\)成立的充要条件是\(gcd(a,b)∣c\)
证明
设\(k = gcd(a,b)\),则 \(k | a\),\(k|b\),根据整除的性质,有 \(k|(ax+by)\)
设\(s\)为\(ax+by\)的最小正数值
再设 \(q = [a / s]\)(\(a\)整除\(s\)的值);\(r = a \mod s = a-q(ax+by) = a(1 - qx)+b(-qy)\);
由此可见\(r\)也为\(a,b\)的线性组合;(\(ax+by\)称为\(a,b\)的线性组合)
又因为\(s\)为\(a,b\)的线性组合的最小正数值,\(0\leq r < s\),所以\(r\)的值为\(0\),即 \(a \mod s = r =0\);\(s | a\);
同理可得 \(s | b\),则 \(s | k\);
又因为 \(k|(ax+by)\),\(s\)为\(ax+by\)的最小正数值,所以 \(k | s\);
因为 \(s|k\),\(k|s\),所以\(s = k\);
原命题得证。
推论
-
\(a\)与\(b\)互质的充要条件是\(\exists x \in \mathbb{Z}\) \(ax + by = 1\)
-
方程\(ax+by = 1\)有解当且仅当整数\(a\)和\(b\)互质
题目
代码
#include <cstdio>
#include <cmath>
int n, s, ans;
int gcd(int x, int y)
{
if (y == 0) return x;
return gcd(y, x % y);
}
int main()
{
scanf ("%d", &n);
for (int i = 1; i <= n; ++i)
{
scanf ("%d", &s);
if (i == 1) ans = s;
else ans = gcd(ans, abs(s));
}
printf ("%d\n", ans);
return 0;
}
扩展gcd
内容
这个算法主要求解上面所述的裴蜀等式:\(ax + by = \gcd(a, b)\)
首先,根据裴蜀定理,该方程一定有整数解
然后我们可以开始推理这个式子,
根据欧几里得算法辗转相除,我们可以得到
又因为
我们知道\(a \mod b = a - a * \:b / \:b\)的,所以会有
展开来,以\(a\),\(b\)为主元
此时,联立(1)式得到
所以我们得到
由于每次辗转相除,\(a\)和\(b\)都在减小,当\(b\)减小到0时,就可以得出\(x = 1\),\(y = 0\),然后我们就可以把它们当做\(x'\)\(和y’\),递归回去求出最开始的那个\(x\)和\(y\)了
特别注意的是,\(y = x' - \:a\:/\:b\: *\: y'\)不能写成了\(y = x' - y'*\:\:a\:/\:b\),我们主元的时候换了个位置,把\(y'\)换到了前面,是为了好理解,如果最后还这样算是会出现精度误差的,不信的同学可以试一试
我讲的是不是特别清楚呀!
题目
练习题1
题意求\(a x \equiv 1 \pmod {b}\)的最小正整数解
仔细观察,我们可以把它转化为求方程\(ax + by = 1\)的\(x\)的最小正整数解
直接用我们的扩展欧几里得就可以了,
但是题目要求最小正整数解,假如求出来的是负数,就手动给他加,怎么加呢
由于题目保证一定有解,则\(\gcd(a,b) = 1\),所以对于我们的方程\(ax+by=1\),对于已经求出来的一组解\(x_1\)和\(y_1\),\(x\)加上\(b\),\(y\)减去\(a\),我们就会得到另一组整数解,这是非常显然的。
因此我们就不断给\(x\)加上\(b\)就行,当然不可能傻傻的去\(while\)地加,
这个加的过程很像取模,它其实等价于\(x = (x\mod b + b) \mod b\),仔细想想哦
code
#include <cstdio>
typedef long long LL;
LL a, b, c, x, y, t;
void ex_gcd(LL A, LL B)
{
if (B == 0)
{
x = 1, y = 0;
return ;
}
LL tmp = x;
x = y;
y = tmp - A / B * y;
}
int main()
{
scanf ("%lld%lld", &a, &b);
ex_gcd(a, b);
x = (x % b + b) % b;
printf ("%lld\n", x);
return 0;
}
练习题2
01
用您聪明的脑袋瓜子易将原题转化为同余方程:\((n - m)t\equiv x- y \pmod p\),\(t\)是跳的次数
怎么用扩展欧几里得呢,
我们令\(a = n-m\),\(b = l\),\(c=x-y\)
此时方程继续转化为\(ax + by = c\),注意这里的\(x\)和\(y\)不是上面那个常数哦,是要求的未知数
02
令 g = \(\gcd(a, b)\),方程有解当且仅当\(c \equiv 0\pmod g\)
为什么呢,回到我们最开始的裴蜀等式:
两边同时乘以\(c/\gcd(a,b)\)得:
这道题里面,我们的\(a\)就是裴蜀等式里的\(ac/\gcd(a,b)\),\(b\)就是裴蜀等式里的\(bc/gcd(a,b)\)
因此我们用扩欧算出来的是裴蜀等式的解而不是这道题的解,于是答案处我们要乘上一个\(c/\gcd(a,b)\)
03
有个坑点,扩欧里的\(a\)和\(b\)都是正整数,当\(a = n - m < 0\)时,就不对了,这个时候就把\(a\)乘个\(-1\),\(c\)也乘个-1就行,因为\(c\)可以不一定是正数
04
最后的解又可能是负数,我们又要想办法把它变成正数
这里我们的\(\gcd(a,b)\)就不一定是1了,此时用什么来‘加’呢
随便举个例子:\(2x + 4y = 4\),有解为\(x1=-2,y1= 0\)
跟它值分布相邻的那一组解是什么呢,就是\(x2 = x1 + 2 = 0,y2=y1-1\)
这个2就是\(b/\gcd(a,b)\),为什么是这样可以自己尝试证明
code
#include <cstdio>
typedef long long LL;
LL N, M, X, Y, L;
LL A, B, C, x, y, G, add;
LL ex_gcd(LL a, LL b)
{
if (b == 0)
{
x = 1, y = 0;
return a;
}
int ret = ex_gcd(b, a % b), tmp = x;
x = y; y = tmp - a / b * y;
return ret;
}
int main()
{
scanf ("%lld%lld%lld%lld%lld", &X, &Y, &M, &N, &L);
A = N - M, B = L, C = X - Y;
if (A < 0) A *= -1, C *= -1;
G = ex_gcd(A, B);//求解的是ax+by=gcd(a,b)
if (C % G) return printf ("Impossible\n"), 0;
add = B / G;
x = (C / G * x % add + add) % add;
printf ("%lld\n", x);
return 0;
}
矩阵加速
规则
矩阵乘法怎么乘的?
上图一目了然
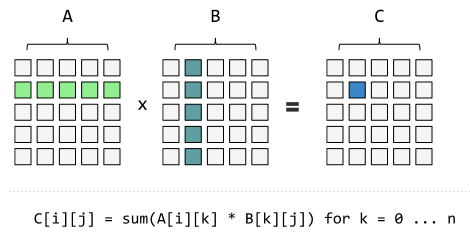
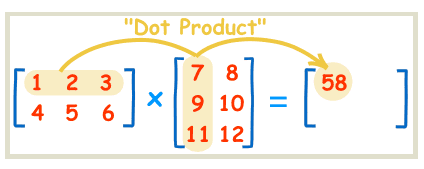
也就是说,矩阵第m行与第n列交叉位置的那个值,等于第一个矩阵第m行与第二个矩阵第n列,对应位置的每个值的乘积之和
即\(c_{i,j} = \displaystyle\sum_{k=1}^na_{i,k}*b_{k,j}\)
题目
练习题1
我们已知\(a_x = a_{x-1} + a_{x-3}\)
因此我们其实就是要推出\(\begin{bmatrix} a_{x-1} \\ a_{x-2}\\a_{x -3}\end{bmatrix}\)乘上一个矩阵得到\(\begin{bmatrix} a_x\\ a_{x-1}\\ a_{x-2}\\ \end{bmatrix}\)
我们可以把\(a_x\),\(a_{x-1}\),\(a_{x-2}\)都用\(a_{x-1}\),\(a_{x-2}\),\(a_{x-3}\)表示出来,如下
所以我们的矩阵便是\(\begin{bmatrix} 1&0 & 1\\ 1 & 0 & 0\\ 0 & 1 & 0\\ \end{bmatrix}\)
但是我们原来的矩阵是一个三行一列的矩阵,而推出来的是个三行三列的矩阵,所以我们只能把原来的矩阵扩充
根据上面两幅图,我们不难发现,在第\(i\)行\(i\)列写上原数即可起到我们想要的效果,即\(\begin{bmatrix} a_{x-1}&0 & 0\\ 0 & a_{x-2} & 0\\ 0&0&a_{x-3}\\ \end{bmatrix}\)
由于最后答案第一个是\(a_{n + 1}\),所以我们输出第二行第一个为\(a_n\)
这种的代码
#include <cstdio>
#include <cstring>
const int MOD = 1e9 + 7;
typedef long long LL;
int T, n;
struct Matrix
{
LL s[5][5];
}base, ans;
inline void init()
{
std::memset(ans.s, 0, sizeof(ans.s));
std::memset(base.s, 0, sizeof(base.s));
for (int i = 1; i <= 3; ++i) ans.s[i][i] = 1;//这里需要仔细想想为什么
base.s[1][1] = base.s[1][3] = base.s[2][1] = base.s[3][2] = 1;
}
inline Matrix work(Matrix a, Matrix b)
{
Matrix c; std::memset(c.s, 0, sizeof(c.s));
for (int i = 1; i <= 3; ++i)
for (int j = 1; j <= 3; ++j)
for (int k = 1; k <= 3; ++k)
c.s[i][j] += (a.s[i][k] % MOD) * (b.s[k][j] % MOD),
c.s[i][j] %= MOD;
return c;
}
int main()
{
scanf ("%d", &T);
while (T--)
{
init(), scanf ("%d", &n);
if (n <= 3)
{
printf ("1\n");
continue;
}
while (n)
{
if (n & 1) ans = work(ans, base);
n >>= 1;
base = work(base, base);
}
printf ("%lld\n", ans.s[2][1]);
}
return 0;
}
其实足够熟练,不需要扩充,直接用\(\begin{bmatrix} a_x\\ a_{x-1}\\ a_{x-2}\\ \end{bmatrix}\)去乘就可以了,这样其实好理解的多,但是由于矩阵大小不同,所以乘起来也有点不同,要写两个乘法
代码
#include <cstdio>
#include <cstring>
const int MOD = 1e9 + 7;
typedef long long LL;
int T, n;
struct Matrix
{
LL s[5][5];
}base, ans;
inline void init()
{
std::memset(ans.s, 0, sizeof(ans.s));
std::memset(base.s, 0, sizeof(base.s));
ans.s[1][1] = ans.s[2][1] = ans.s[3][1] = 1;
//for (int i = 1; i <= 3; ++i) ans.s[i][i] = 1;//这里需要仔细想想为什么
base.s[1][1] = base.s[1][3] = base.s[2][1] = base.s[3][2] = 1;
}
inline Matrix work(Matrix a, Matrix b, int opt)
{
Matrix c; std::memset(c.s, 0, sizeof(c.s));
if (opt == 1)
{
for (int i = 1; i <= 3; ++i)
for (int j = 1; j <= 3; ++j)
for (int k = 1; k <= 3; ++k)
c.s[i][j] += (a.s[i][k] % MOD) * (b.s[k][j] % MOD),
c.s[i][j] %= MOD;
}
else
{
for (int i = 1; i <= 3; ++i)
for (int j = 1; j <= 3; ++j)
c.s[i][1] += (a.s[j][1] % MOD) * (b.s[i][j] % MOD),
c.s[i][1] %= MOD;
}
return c;
}
int main()
{
scanf ("%d", &T);
while (T--)
{
init(), scanf ("%d", &n);
if (n <= 3) {printf ("1\n"); continue; }
n -= 3;//注意,由于ans[1][1],ans[2][1],ans[3][1]都设为了1,所以是a[3]从开始的
while (n)
{
if (n & 1) ans = work(ans, base, 0);
n >>= 1;
base = work(base, base, 1);
}
printf ("%lld\n", ans.s[1][1]);
}
return 0;
}
练习题2
记得开long long!
#include <cstdio>
#include <cstring>
typedef long long LL;
const int N = 100 + 30;
const int MOD = 1e9 + 7;
int n;
LL K;
struct Matrix
{
LL s[N][N];
}a, b;
Matrix mul(Matrix x, Matrix y)
{
Matrix c; std::memset(c.s, 0, sizeof(c.s));
for (int i = 1; i <= n; ++i)
for (int j = 1; j <= n; ++j)
for (int k = 1; k <= n; ++k)
c.s[i][j] += (x.s[i][k] % MOD) * (y.s[k][j] % MOD),
c.s[i][j] %= MOD;
return c;
}
int main()
{
scanf ("%d%lld", &n, &K);
for (int i = 1; i <= n; ++i)
for (int j = 1; j <= n; ++j)
scanf ("%lld", &a.s[i][j]);
b = a, K--;//想想为什么要减1
while (K)
{
if (K & 1) a = mul(a, b);
K >>= 1;
b = mul(b, b);
}
for (int i = 1; i <= n; ++i)
{
for (int j = 1; j <= n; ++j) printf ("%lld ", a.s[i][j]);
printf ("\n");
}
return 0;
}
乘法逆元
定义
若在\(\mod p\)的意义下,对于一个整数\(a\),有\(a \times b \equiv 1\pmod p\),那么这个整数b即为a的乘法逆元,同时a也为b的乘法逆元
一个数有逆元的充分必要条件是\(\gcd(a, p)=1\),此时\(a\)才有对\(p\)的乘法逆元[^1 ]
[^1 ]: 所以我们经常借助它来进行\(\frac{a}{b} \pmod p\)的运算
作用
除法是不能取模的,即\(a \div b \mod p \ \neq \ (a\mod p \ \div \ b \mod p) \mod p\)
逆元可以解决这个问题
由于取模运算对于乘法来说是成立的,所以逆元就是把除法取模转化为乘法取模
设\(x\)满足
模运算对乘法成立,对(1)式两边同时乘\(b\),得
如果\(a\)与\(b\)均小于模数\(p\)的话,上式可以改写为
等式两边再同时乘以\(x\),联立(2)式比较得到
因此可以得到
\(x\)就是\(b\)的逆元,\(x\)在模运算的乘法中等同于\(\frac{1}{b}\),这就是逆元的意义
故我们发现,求\((a \div b)\mod p\)等同于求\(a\times (b的逆元) \mod p\)
求法
01费马小定理
内容
即如果\(p\)是质数而整数\(b\)不是\(p\)的倍数,则有\(b^{p-1} \equiv 1\pmod p\)
由于OI中模数总是质数,所以可以用它直接得到\(x \equiv b^{p-2}\)
所以\(b^{p-2}\)即为\(b\)在mod \(p\)意义下的逆元
我们可以用快速幂
code
LL POW(LL s, LL k)
{
LL ans = 1;
while (k)
{
if (k & 1) ans = ans * s % MOD;
a = a * a % MOD;
k >>= 1;
}
return ans;
}
LL Inverse_Element(LL a)
{
return POW(a, MOD - 2);
}
02扩展欧几里得
内容
如果\(bx \mod p = 1\),那么\(bx + py = 1\)
直接扩展欧几里得求解就行啦,其实只有80pts
code
#include <cstdio>
typedef long long LL;
LL n, p, x, y;
inline void ex_gcd(LL a, LL b)
{
if (b == 0)
{
x = 1, y = 0;
return ;
}
ex_gcd(b, a % b);
int tmp = x;
x = y; y = tmp - a / b * y;
}
int main()
{
scanf ("%lld%lld", &n, &p);
for (int i = 1; i <= n; ++i)
{
ex_gcd(i, p);
x = ((x + p) % p) % p;
printf ("%lld\n", x);
}
return 0;
}
03线性算法
式子
证明
令
则有
两边同时乘\(i^{-1}*r^{-1}\)得
移项
带入\(k = p/i\),\(r = p \mod i\)
由于\((p \mod i) < i\),所以在求出\(i^{-1}\)之前,我们早已求出\((p \mod i)^{-1}\);
用数组\(inv[i]\)记录\(i^{-1}\),则
我们还要保证\(i^{-1}>0\),所以我们在(1)式右边加上\(p\),不会影响答案,则
初始\(inv[1] = 1,inv[0] = tan90°=0\)
Code
#include <cstdio>
typedef long long LL;
const int N = 3e6 + 30;
LL n, p, inv[N];
int main()
{
scanf ("%lld%lld", &n, &p);
inv[1] = 1; printf ("%lld\n", inv[1]);
for (LL i = 2; i <= n; ++i)
inv[i] = p - p / i * inv[p % i] % p,
printf ("%lld\n", inv[i]);
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号