大二学习内容-cnblog

离散数学

第9章 关系

英译单词

1. relations and their properties 关系及关系性质
2. ordered pair 有序对或序偶数
3. product set /Cartesian product 笛卡尔积

易混知识

关系

自反关系只要求满足集合A中任意元素有自环或关系矩阵对角线为一

---

反自反

定义（一个不是自反的关系不一定是反自反），每个元素都无环

\[\forall \mathcal{a}\in \mathcal{A},\left ( \mathcal{a},\mathcal{a}\right )\notin \mathcal{R} \]

---

对称关系

​ （可以是空集,关系举证满足1对称分布即可）

\[\mathcal{R}= {\mathcal{R}}^{-1} \]

---

反对称关系

（可以是空集，除对角线外都为0，恒等关系既是对称的也是反对称的）

\[if\left ( \mathfrak{a},\mathfrak{b}\right )\in \mathcal{R}\land \left ( \mathcal{b},\mathcal{a}\right ) \in \mathcal{R}, so \mathcal{a}= \mathcal{b} \]

---

非对称关系

（注意任意性，）

\[\forall \mathcal{a}\forall \mathcal{b} \left ( \mathcal{a},\mathfrak{b}\right ) \in \mathcal{R}\dashrightarrow \left ( \mathcal{b}，\mathcal{a}\right )\notin \mathcal{R} \]

---

关系合成

​ SoR表示R与S的关系合成

闭包（closure）

自反闭包、对称闭包、传递闭包

\[\mathcal{R}\cup {\mathcal{I}}_{\mathcal{a}}，\mathcal{R}\cup {\mathcal{R}}^{-1}， \mathcal{R}\cup {\mathcal{R}}^{2}\cup {\mathcal{R}}^3....\cup{\mathcal{R}}^{\mathcal{n}} \]

---

传递闭包中每一次乘方，就会缩短a,b之间1的路径距离

---

沃舍尔算法（warshalll）

第9章 群

补充前言知识+瞻望

​ 串中^表示单位元（空序列）

(A* , ·) 称为由A生成的自由半群，其中 · 是连接运算，A*是串的集合

第一节 二元运算

定义

​ 集合A上的二元运算是一个处处有定义的函数f:AxA->A;二元运算具有封闭性

​ 延申：n元运算

例题

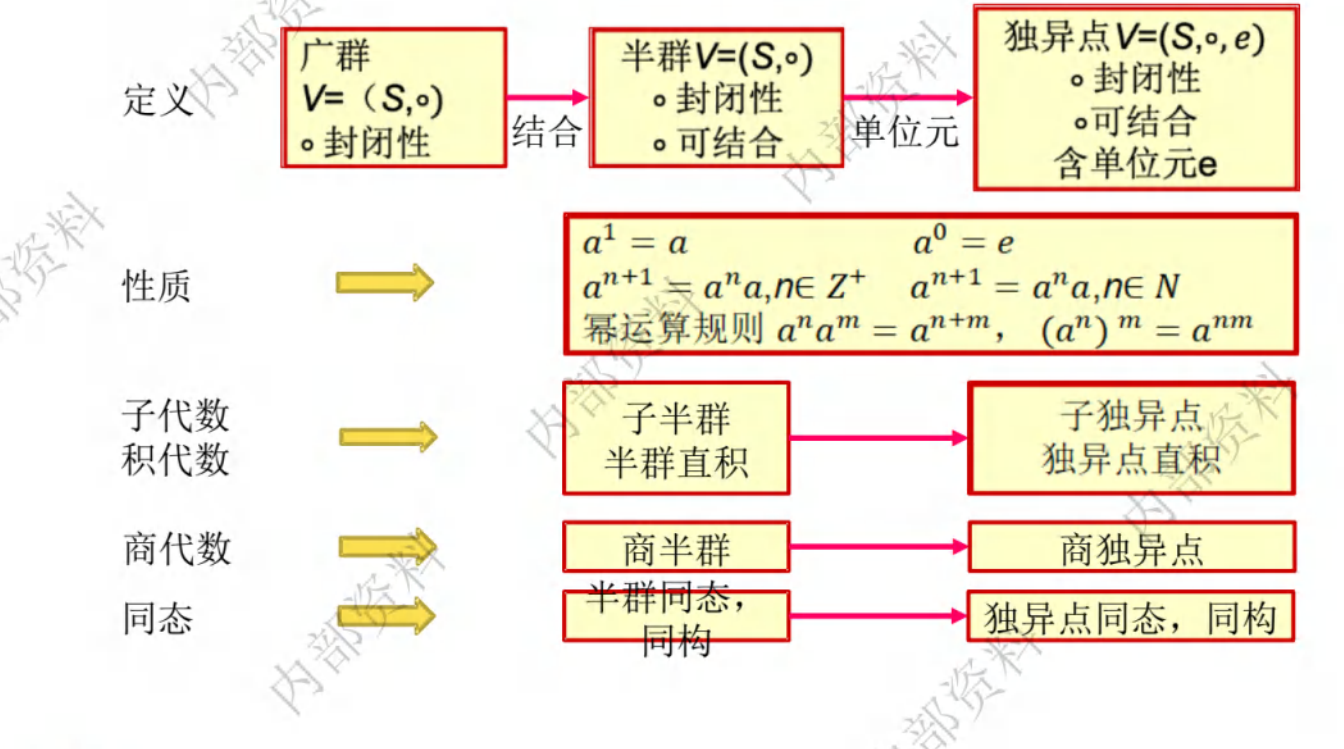
第二节 半群

​ 广群定义：代数系统（S,*),如果S是非空的且*是封闭的，则称（S,*)为广群

​ 半群定义 ：非空集合S和定义在S上可以结合的二元运算 *,如果 *是交换的，那么（S,*)是一个交换半群

​ a*e=e*a=a,则e为单位元（幺元，identity)，且唯一

​ 有单位元(幺元）的半群称作独立点（含幺半群）

​ 含有半群幺元的子半群是子独立点（子幺半群）

​

​ a的n次幂定义为a*a……;

​ 由a的幂次运算可以构造（S,*)的 生成子半群和生成子独立点

幂次构造子半群（与后面构造商半群概念联系紧密）

​

​ 同构 函数f满定义，单射，满射，积的像等于像的积

​ 同态 函数f满定义，积的像等于像的积 （ 同态像，需要满足满射）

第三节 半群的积和商

直积，构造积半群

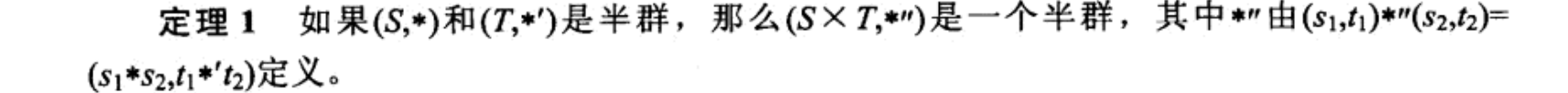
直积的独立元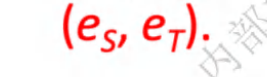

等价关系——>同余关系

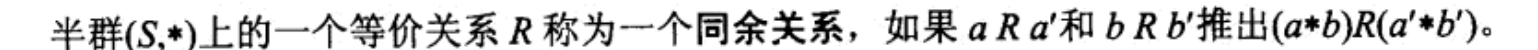
例题

​ 构造商半群

及其性质 对于商半群的运算，实际的*运算是原来半群的运算，只不过现在需要表示为以等价同余关系R划分的等价类代表元，

可以理解为([a] * [b])=[a]*[b]=[[a]*[b]=[a*b],即[a]*[b]=[a*b]

可以理解为商集中的代表元运算后仍然是代表元，也就是经过运算后仍然是一个等价类

例题如下

应该注意到这一点(后面可以知道，Zn是一个阿贝尔群)

自然同态(注意是满射)

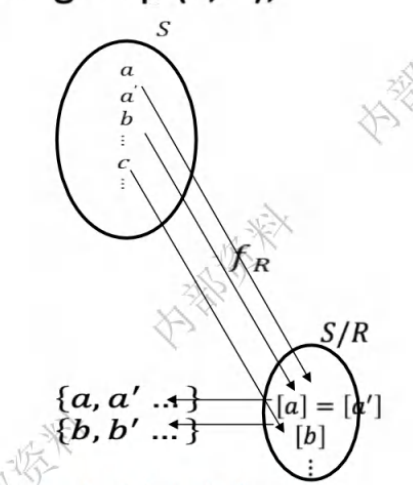
同态基本定理

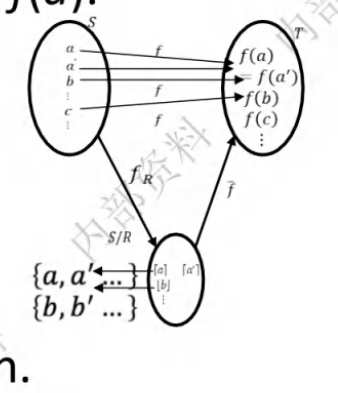
第四节 群

基本群

群的定义 ：(G,*) , *封闭且可以结合，每个元素都有且仅有一个逆元

阿贝尔群：在群的基础上满足运算交换

群的常用术语（第四点是拉格朗日定理）

关于群的元素的一些性质运算，

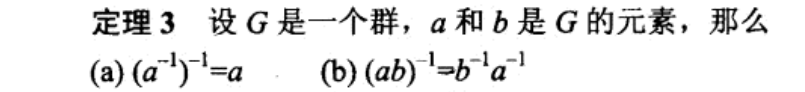
由此可以引出构造子群的方法，幂次构造

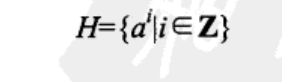
由以上可以得到 任一元素b在运算表里每一行仅仅出现一次，即运算表的每一列或者每一行都是G中所有元素的一种排列

群的阶

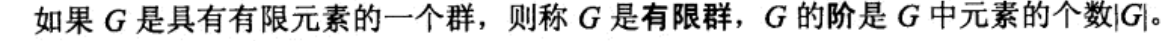
例题 ：函数复合置换，注意行标是外层函数，列标是内层函数

例题中应该注意到的点

第五节群的积和商

直积 （注意不是等于号，而是同构符号）

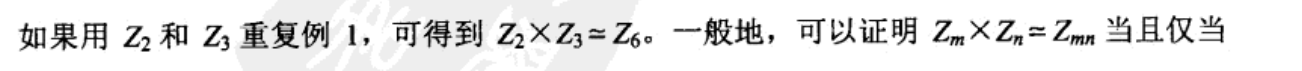
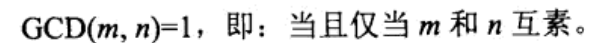
陪集（不是子群或则群） 和正规子群

应该注意到

陪集不一定是G的子集；很显然，陪集的元素数量和子集是相同多的，元素是一一对应的。

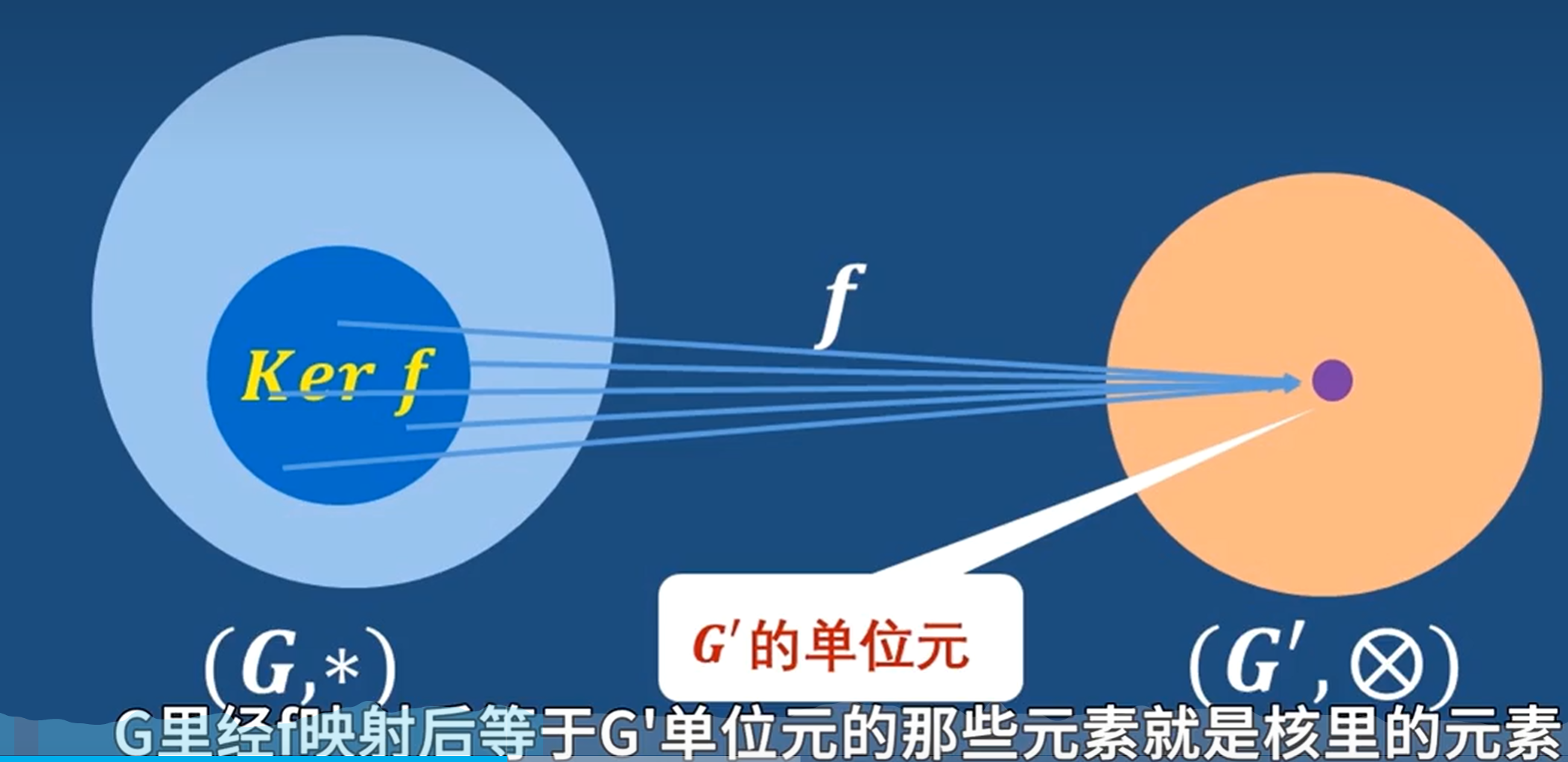
正规子集既是群单位元入驻的陪集，也是商群的单位元，还是自然映射（f(a)=[a]）的同态核

同态核

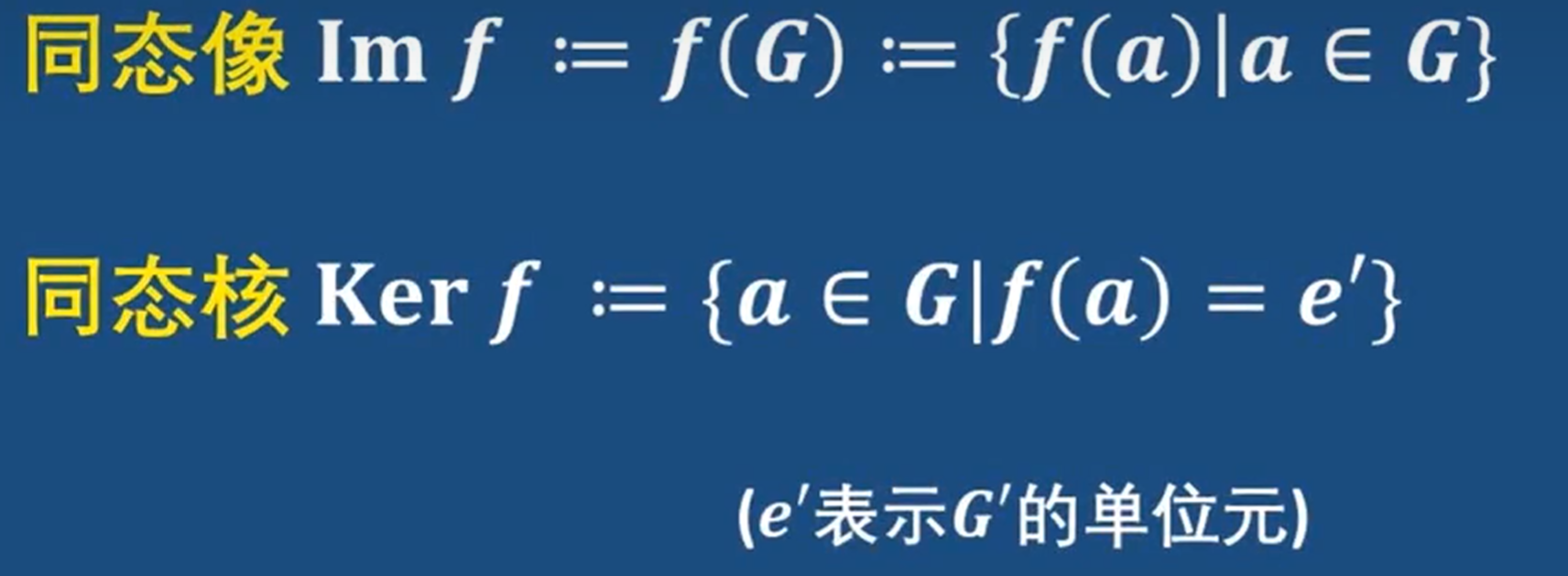
数字电路

数字电路知识前言

译码器和数据选择器的运用

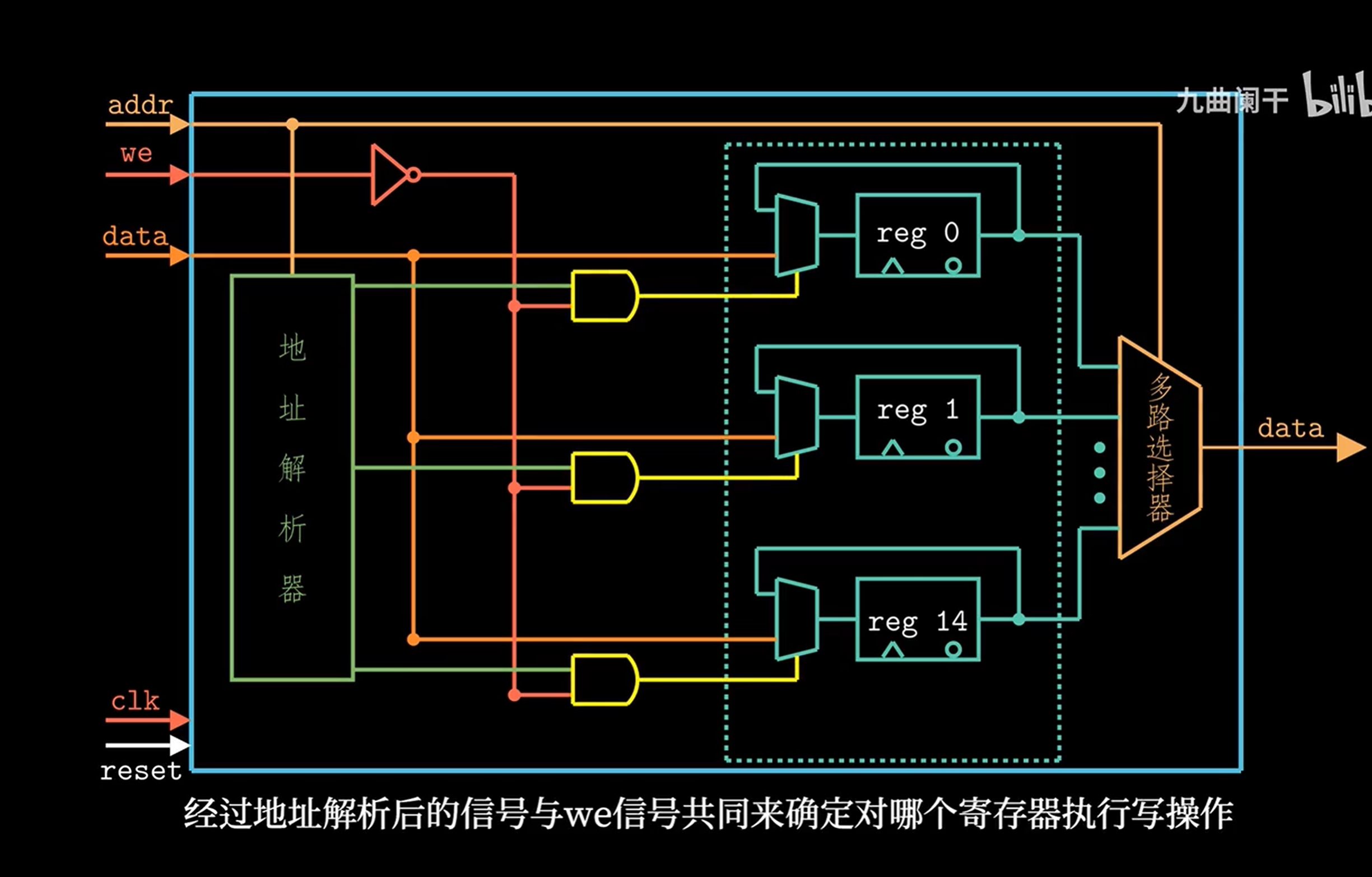
CMOS管

第二章 组合逻辑

数据选择器

典型例子（应该记住有几个使能端）

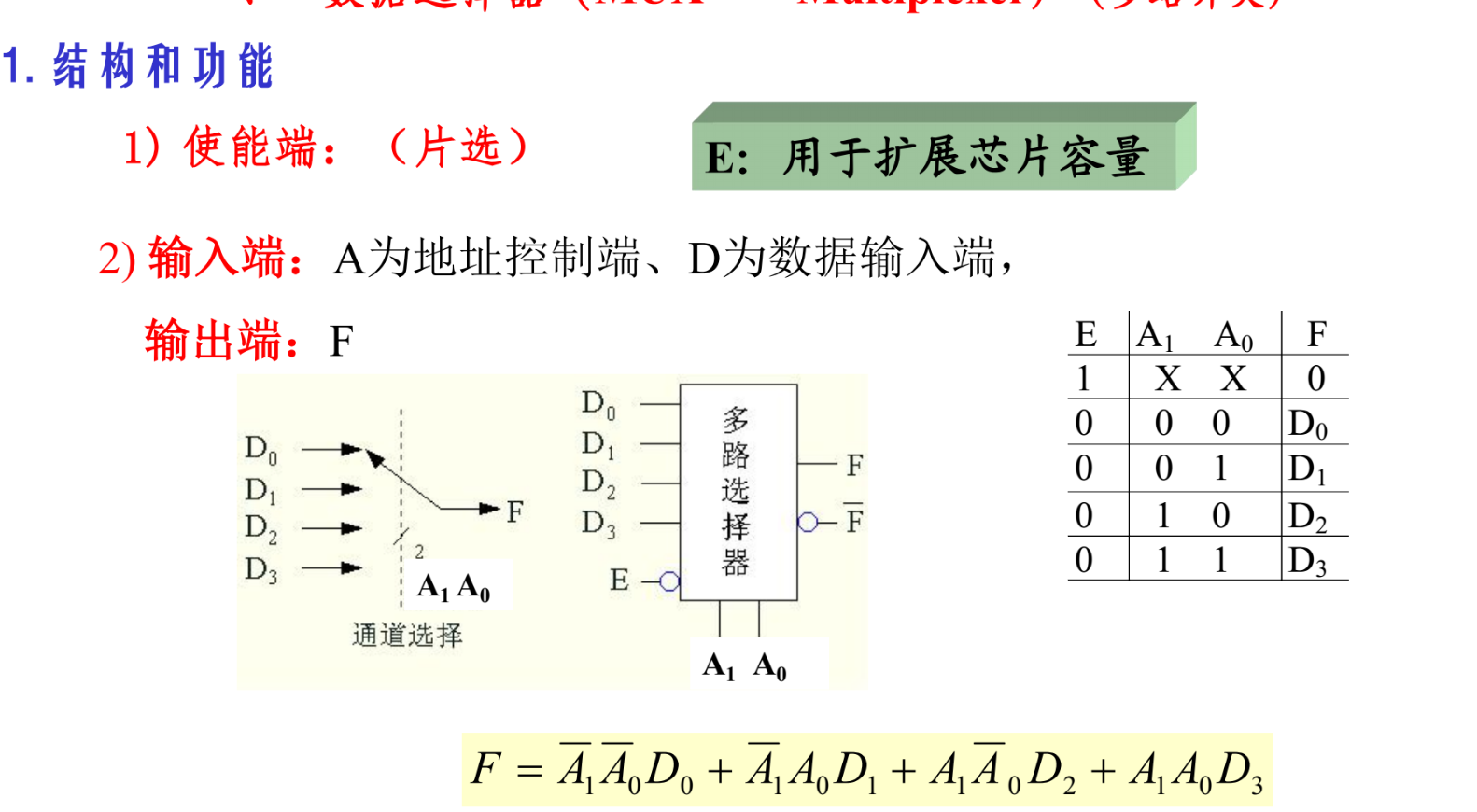
双四选一

八选一

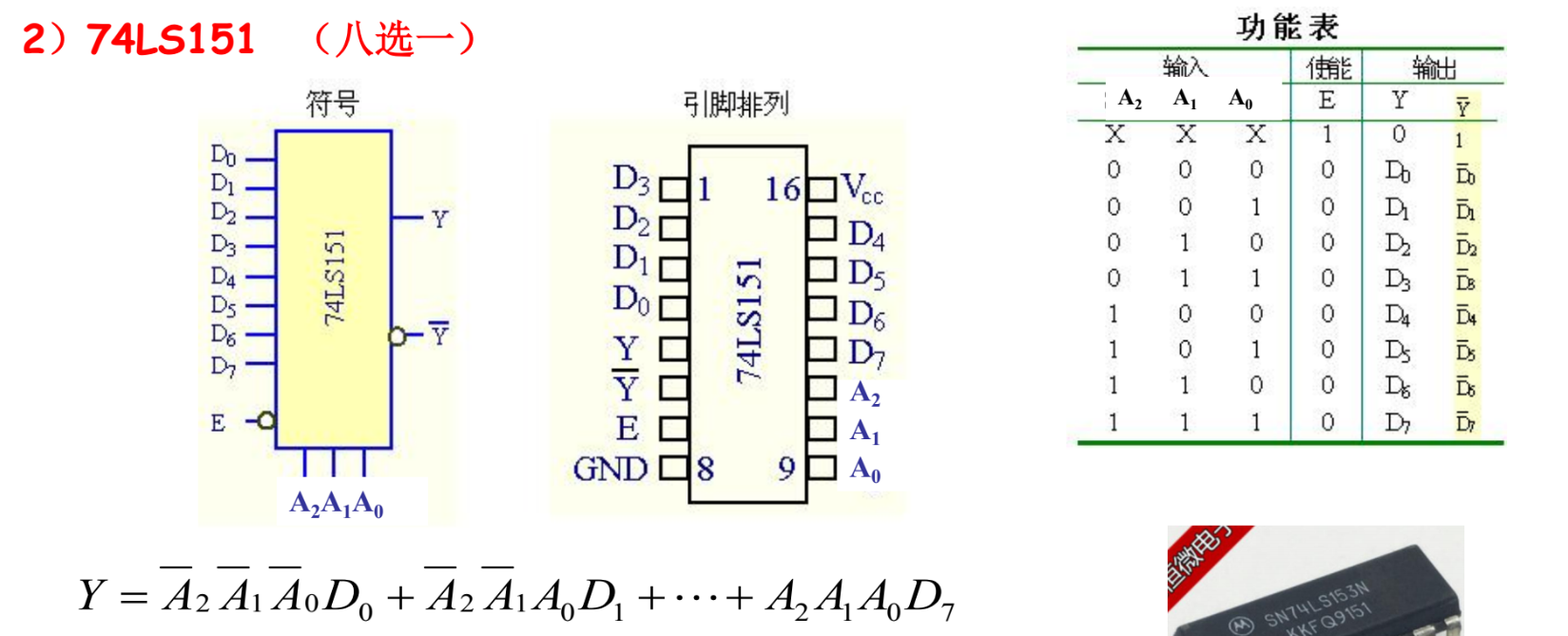
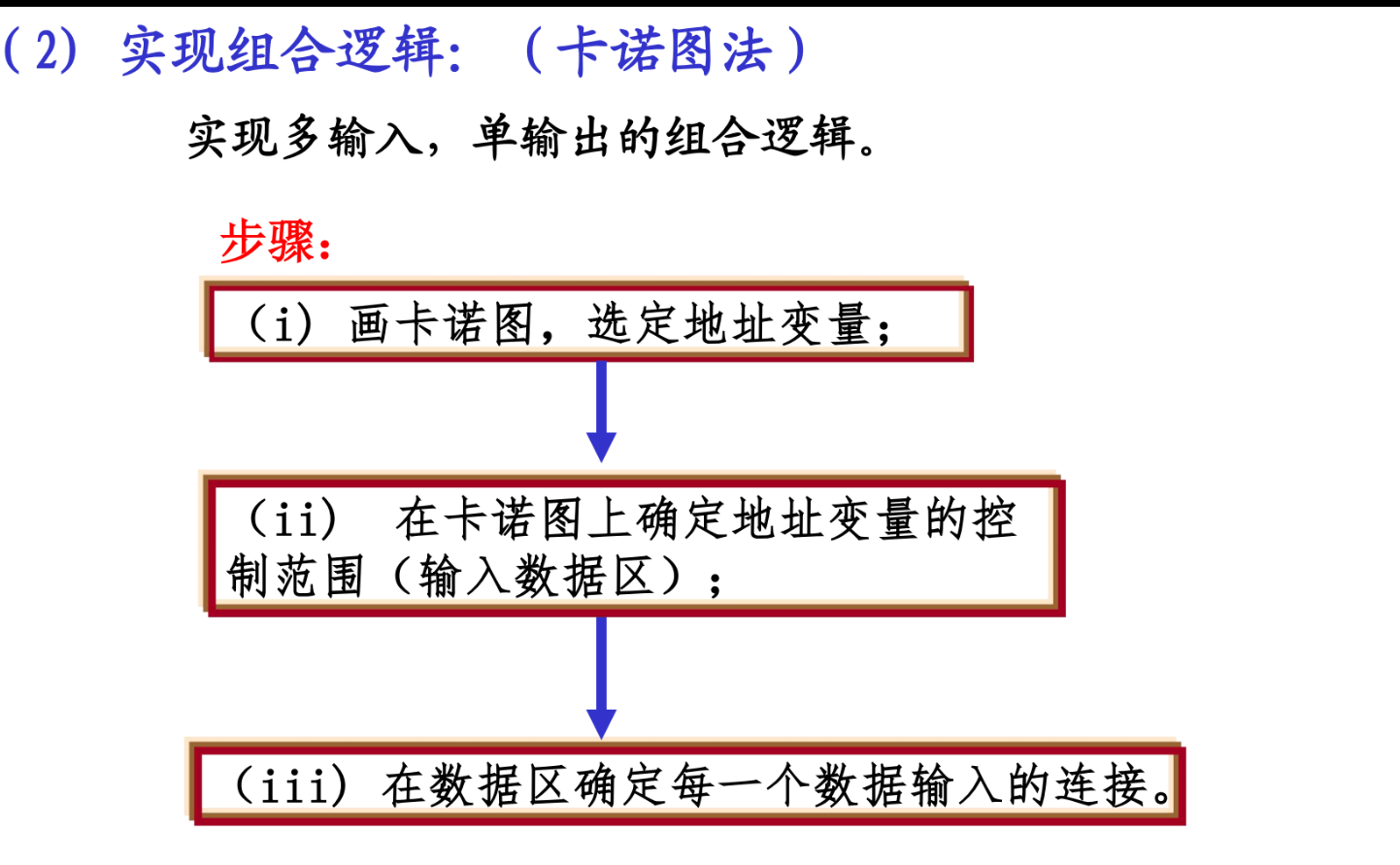
如何实现组合逻辑

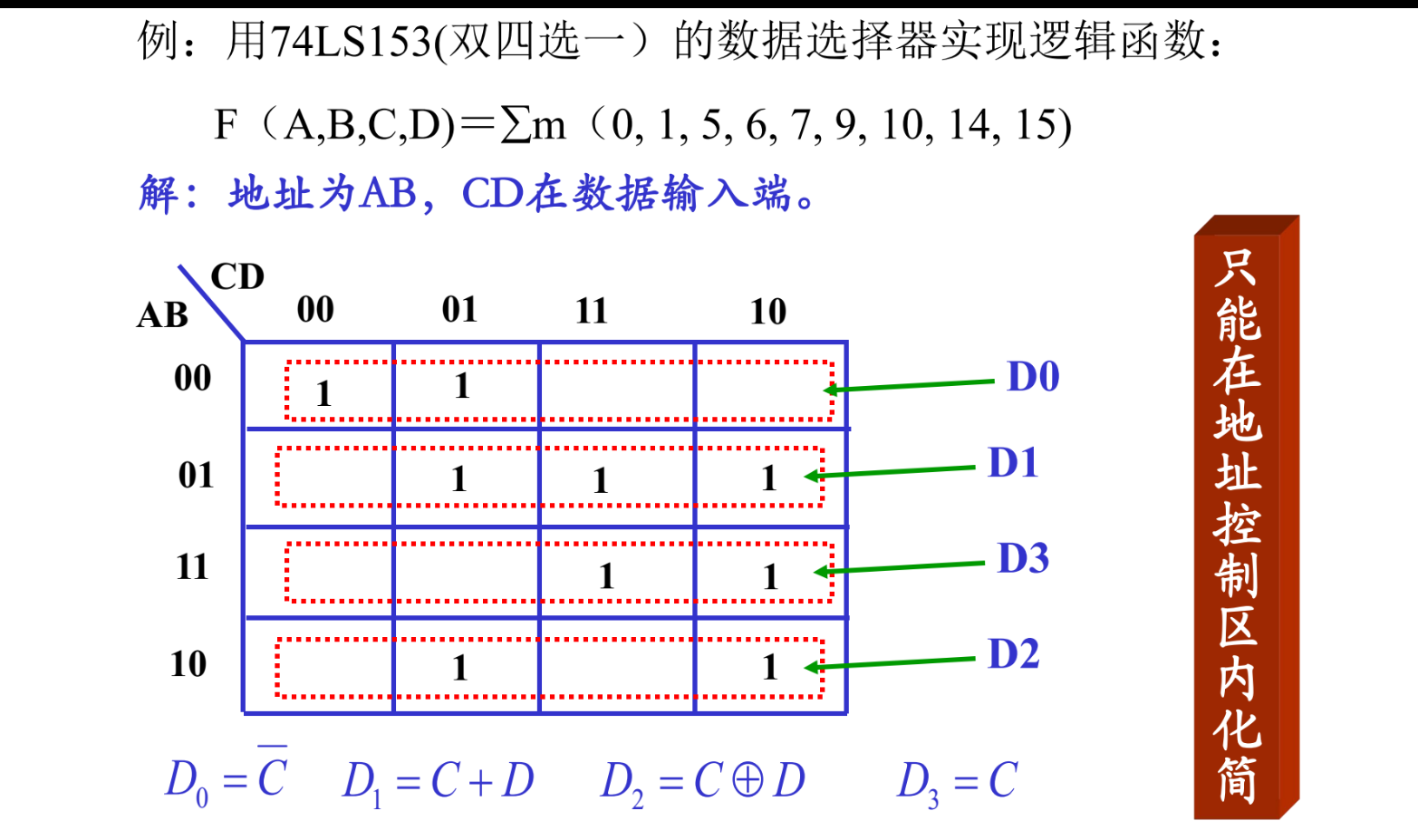
易错点（同一行为一个数据输入端化简，注意D3和D2位置）

四选一

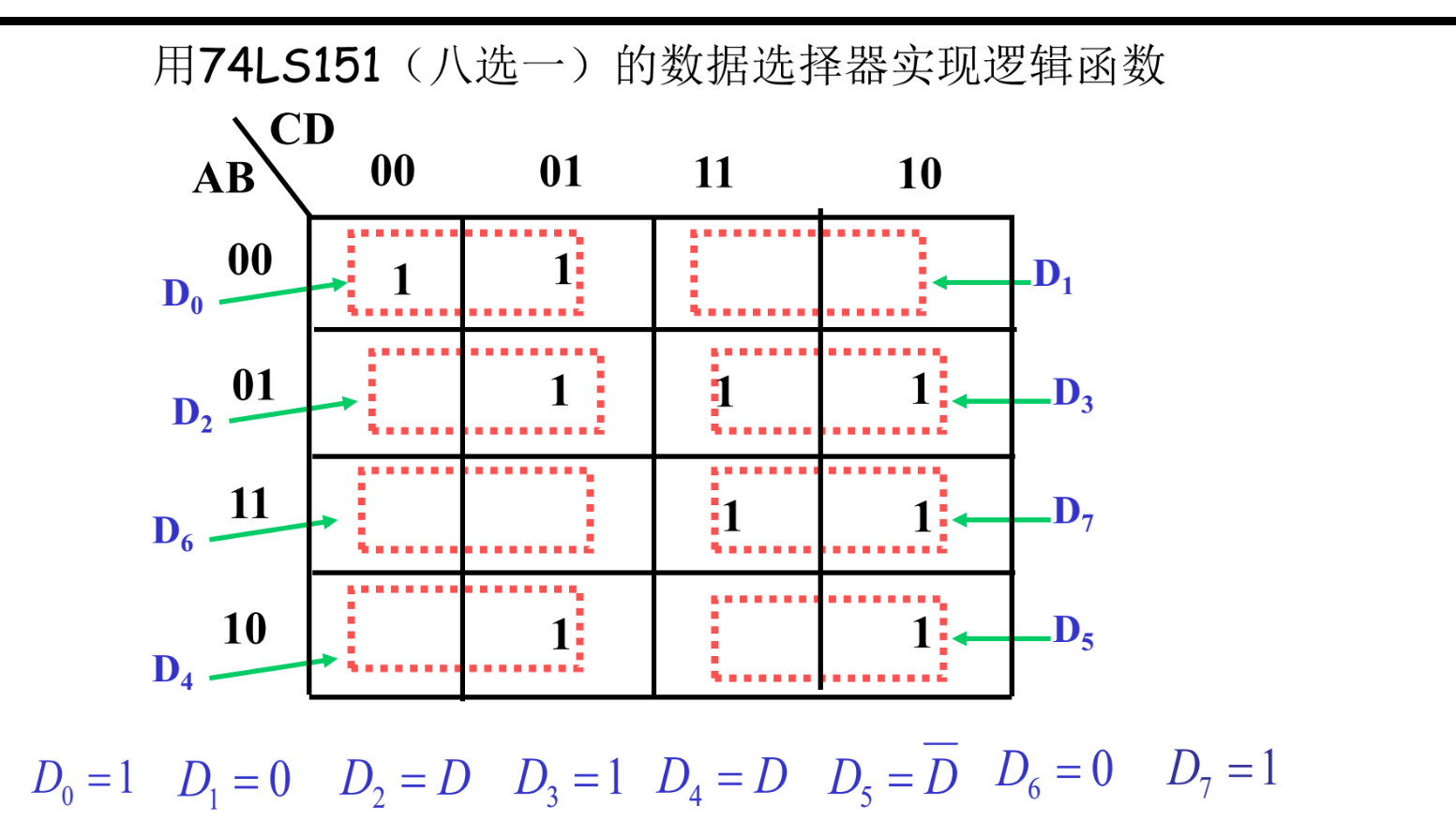
八选一

数据选择器的特点

译码器

译码器种类

（74138--3:8译码器,74LS139)

译码器功能总结

译码器的输出

译码器的输出段对应一个最小项的非

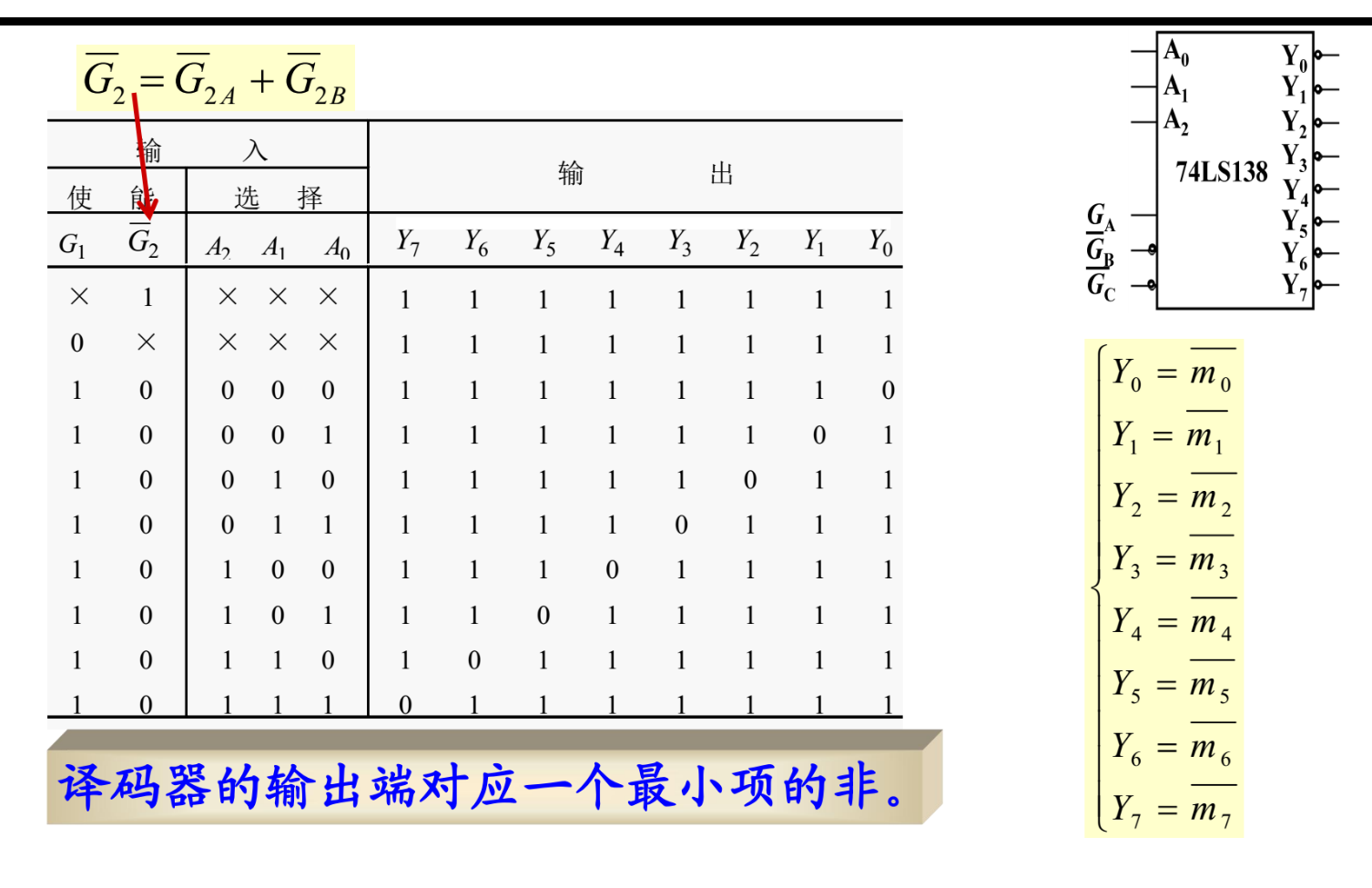
译码器的应用

译码器的扩展（**地位由3-8译码器共用，多余高位（通过译码器或直接）用于片选输出端译码器使能端****）

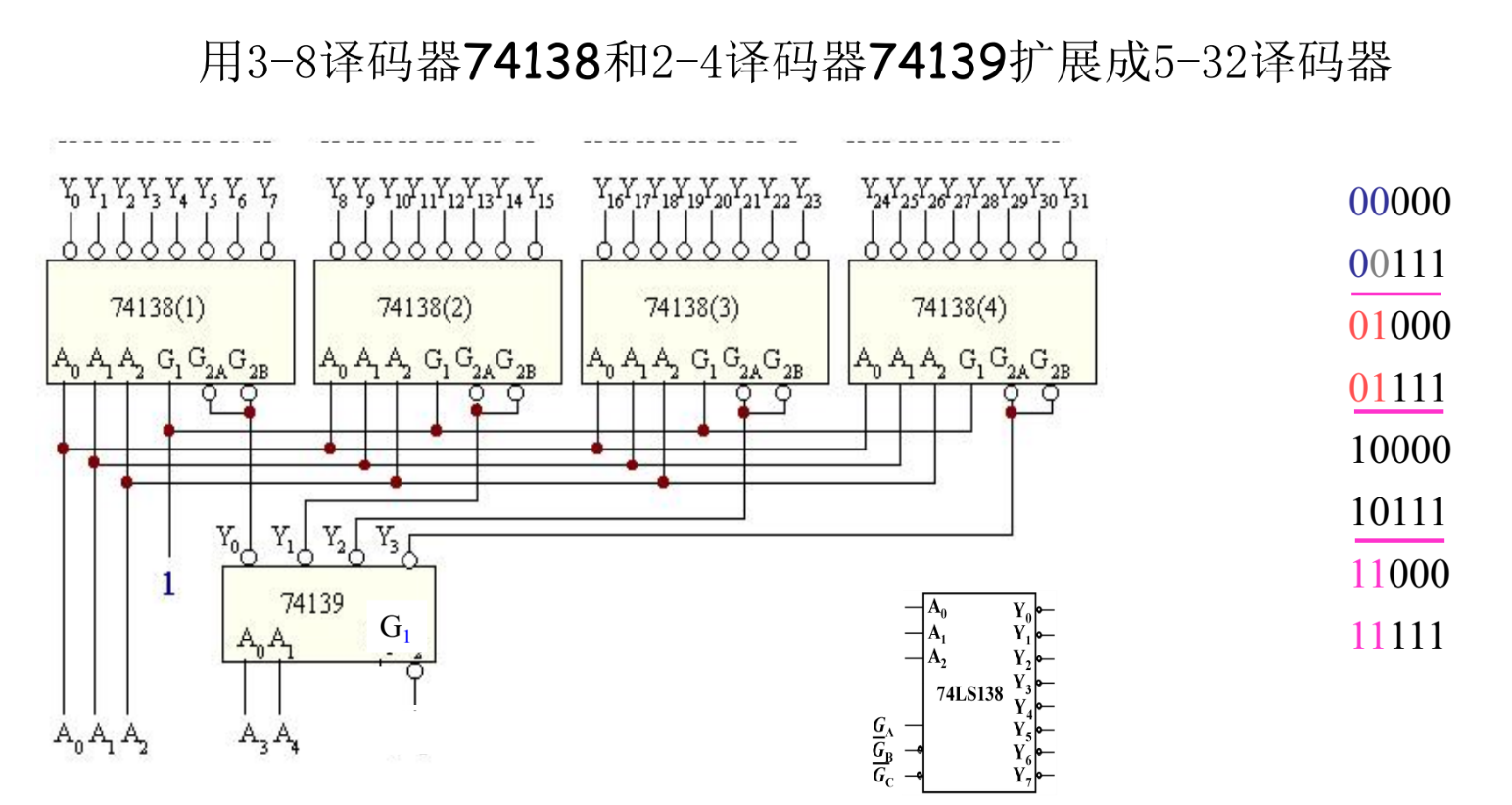
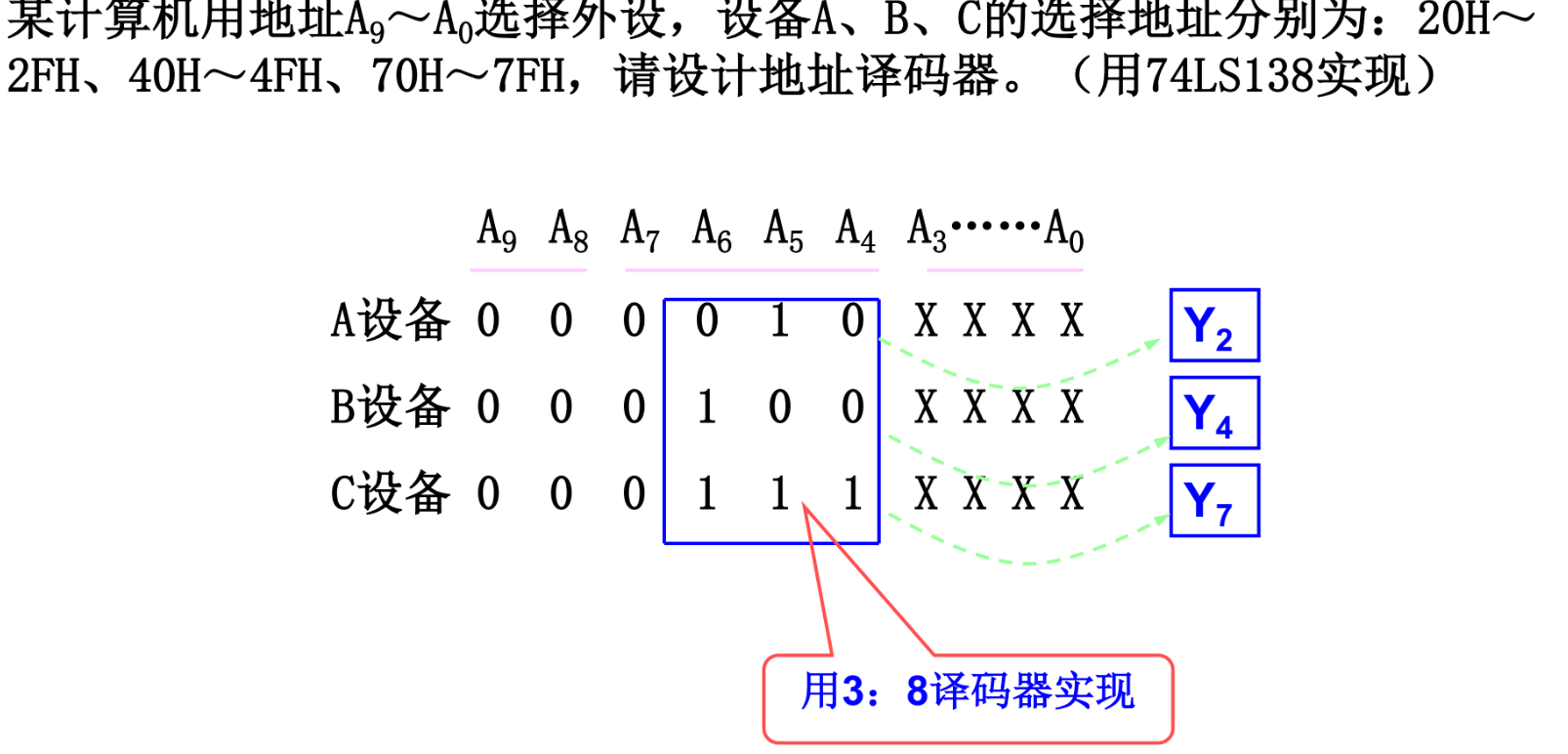
地址译码

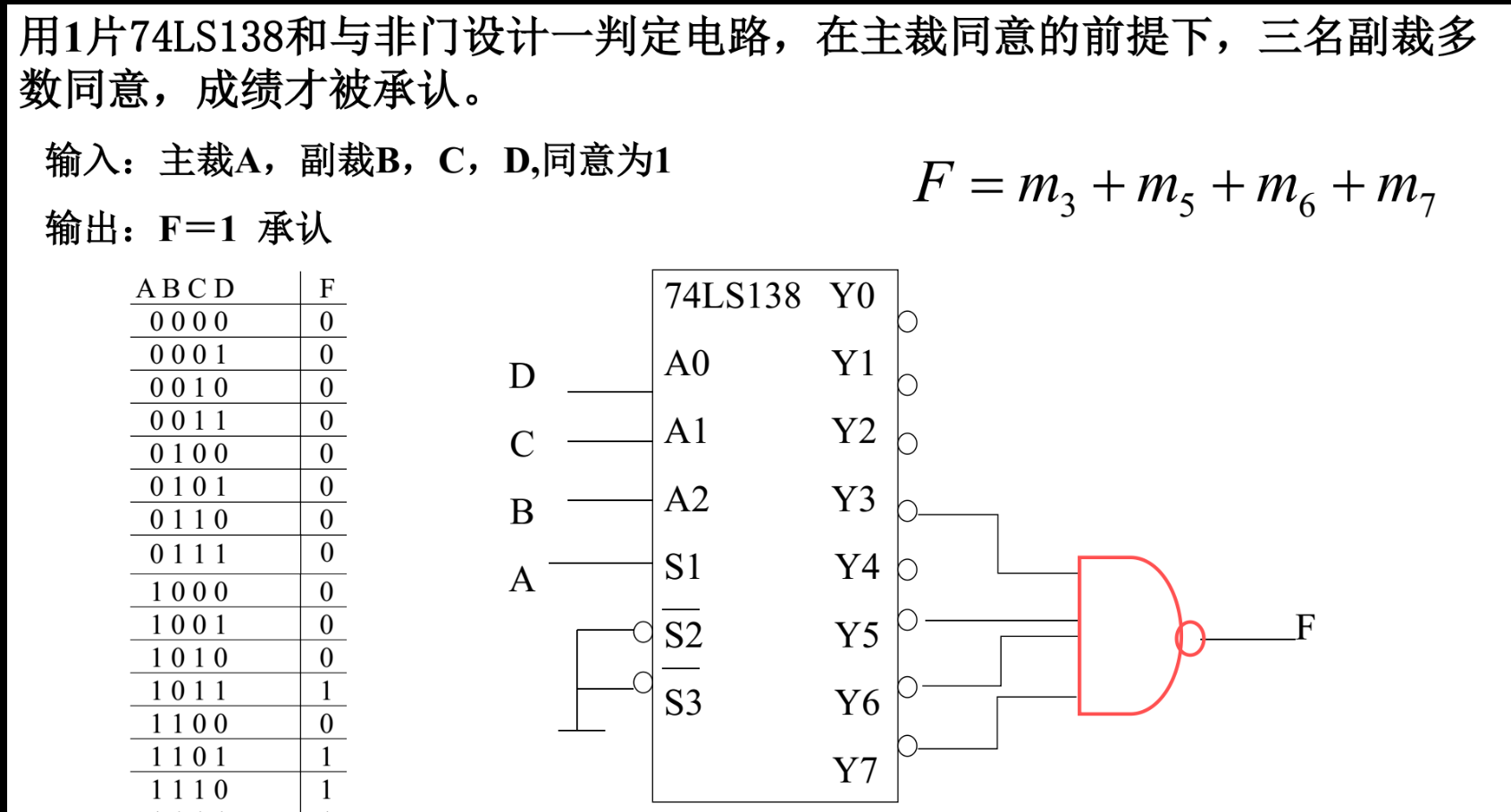
实现逻辑函数（直接用与非）

译码器作数据分配器（使能端变成数据输入端）

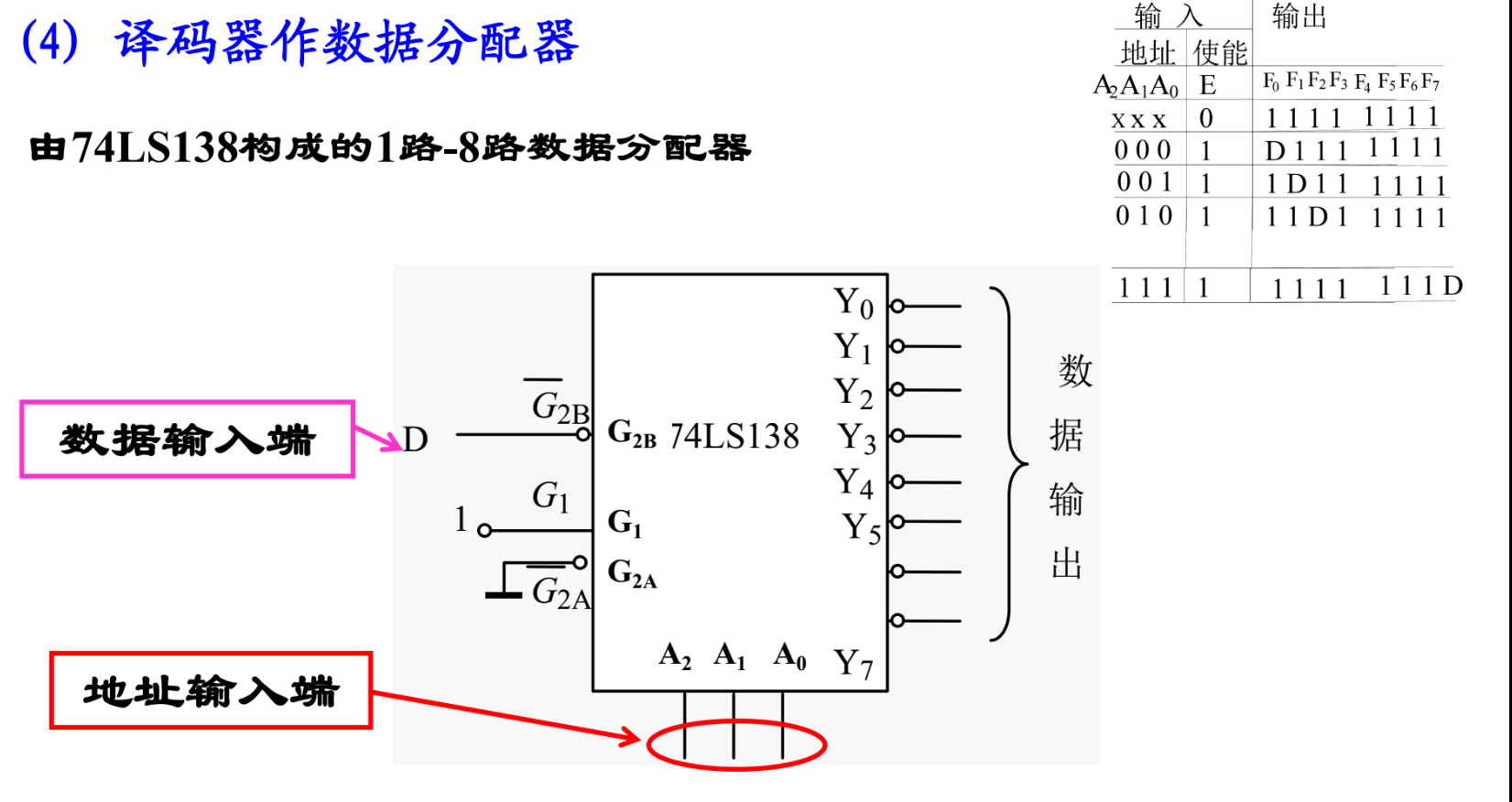
7端显示译码器（共阴级表示阴极已经接好）

显示译码器

可知测试均为低电平有效，LT低电平且熄灭BI高电平无效，灯全亮，RBO为输出端，与BI输入共用引脚）

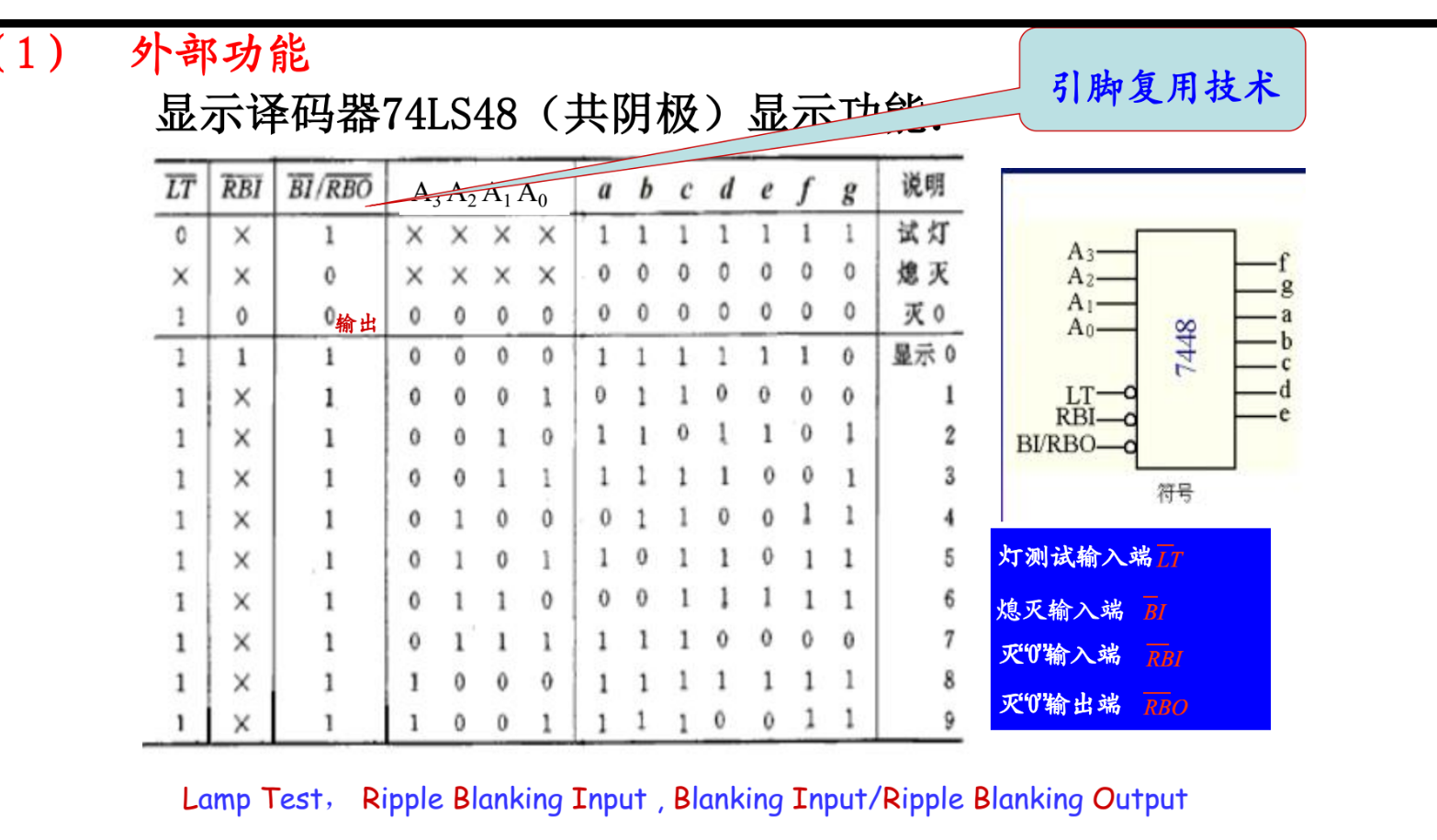
74LS148

编码器

分类

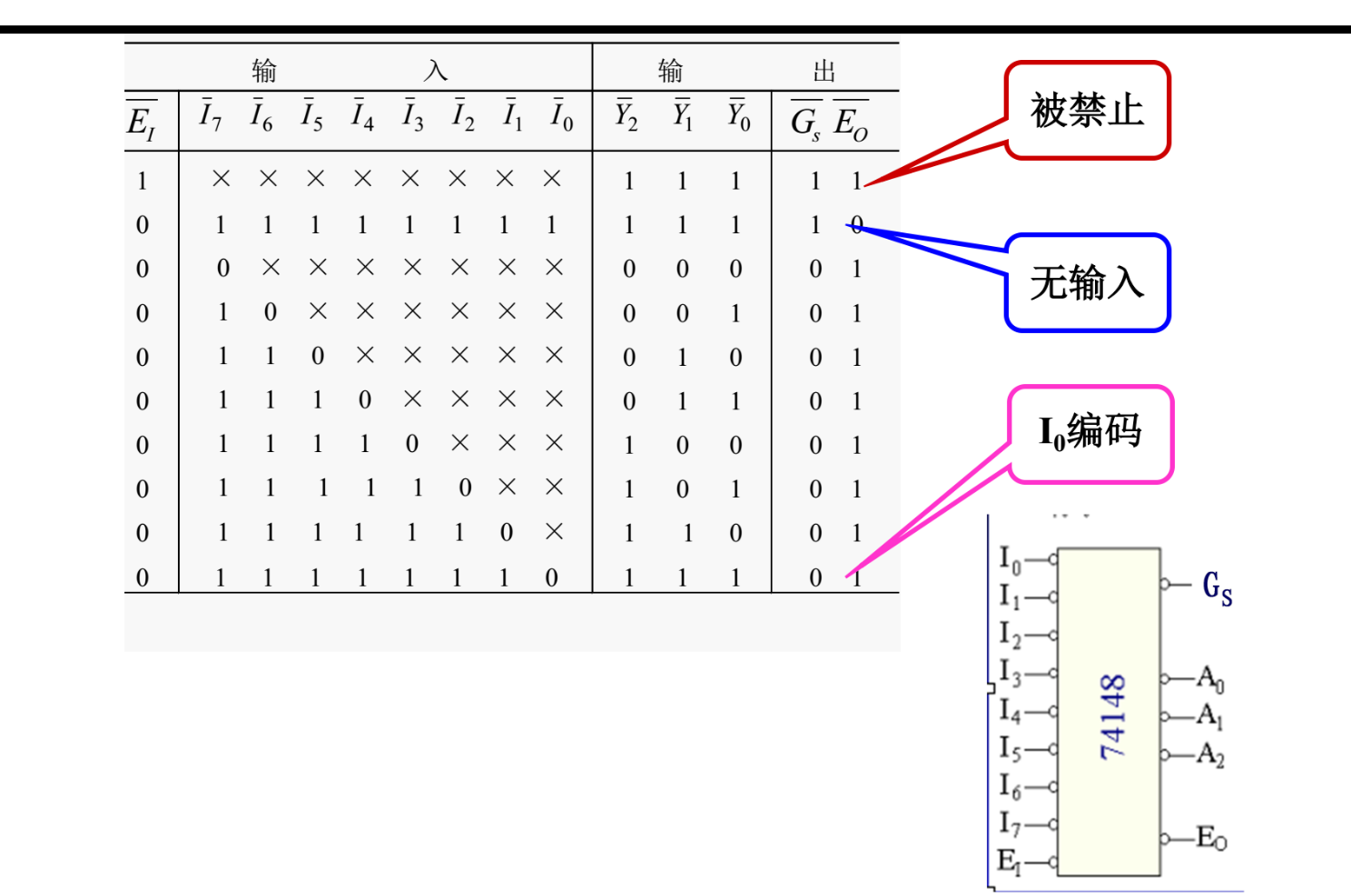
二—十（其实叫做十—二进制优先编码更合适）

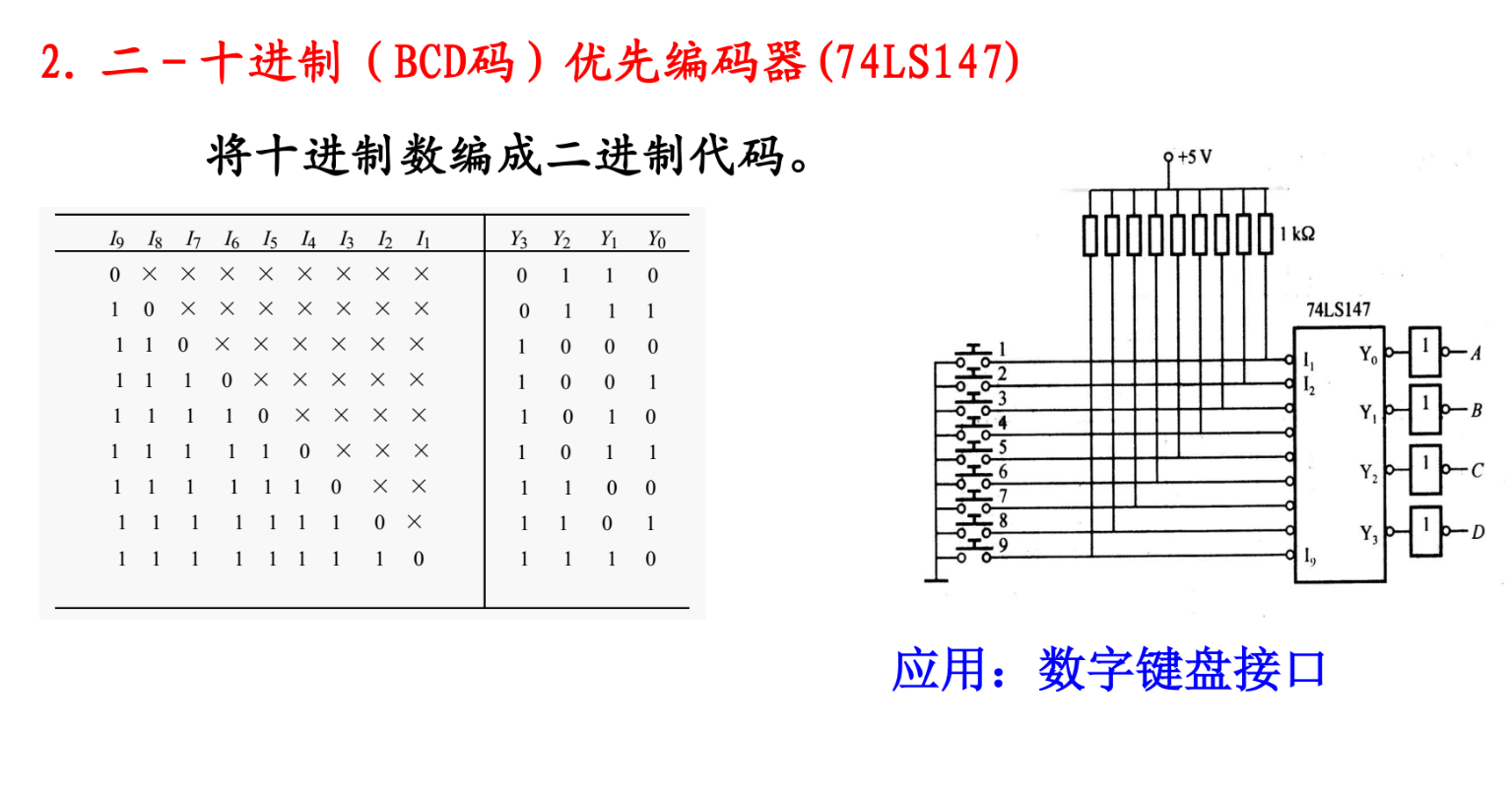
​ 八——三进制编码器

真值表（注意第一行和第二行）

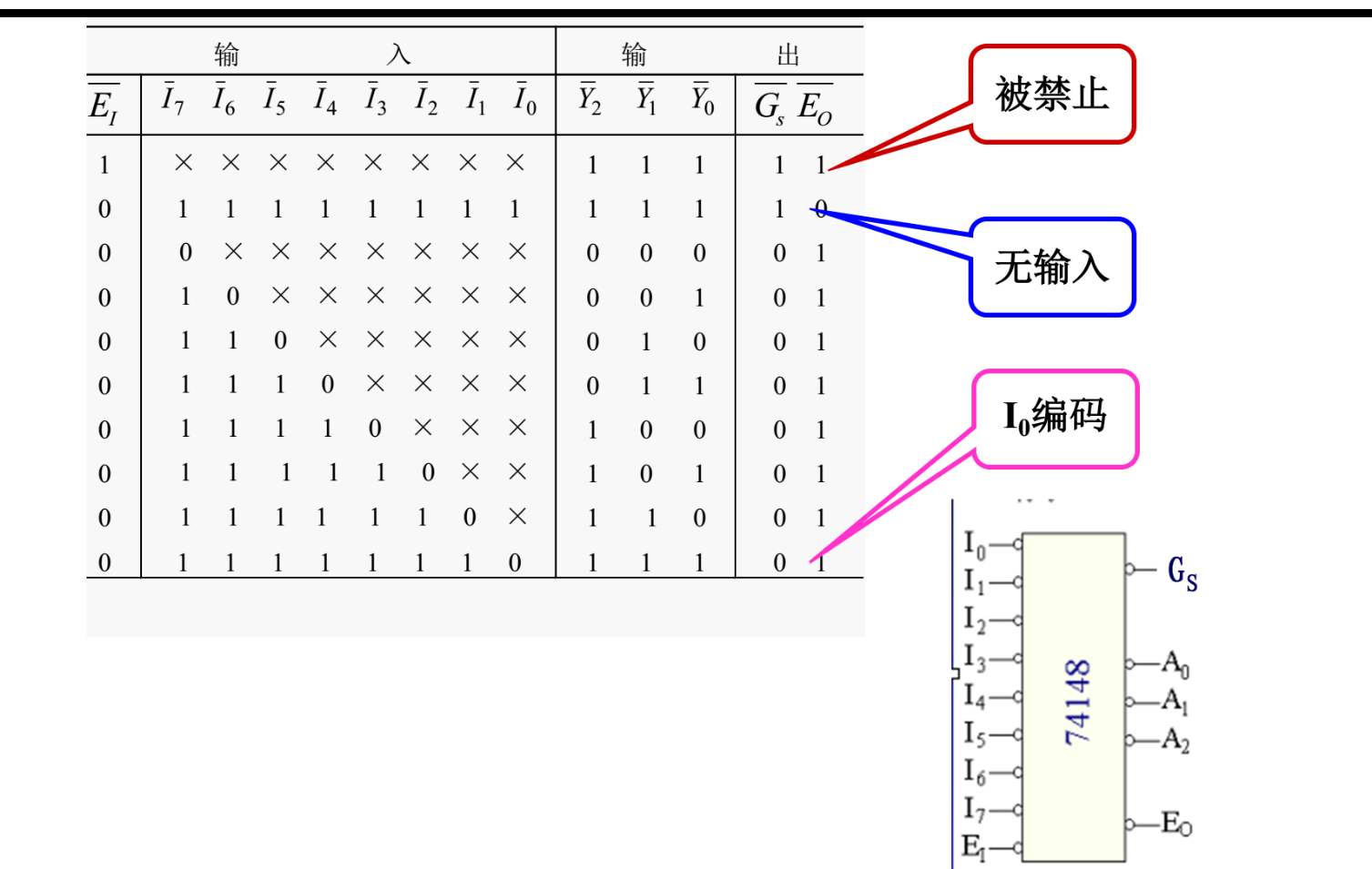
可以利用使能端扩容

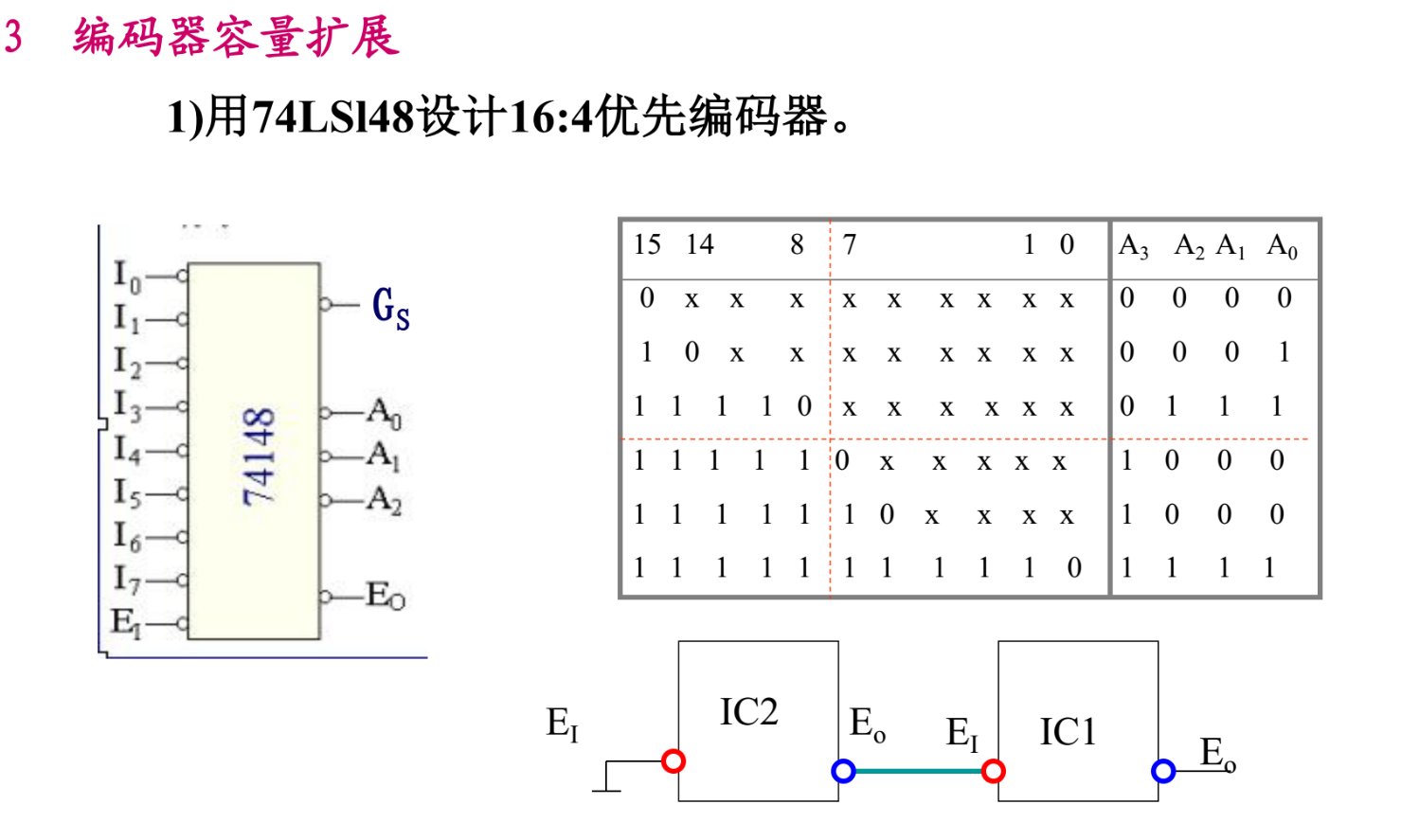
例题

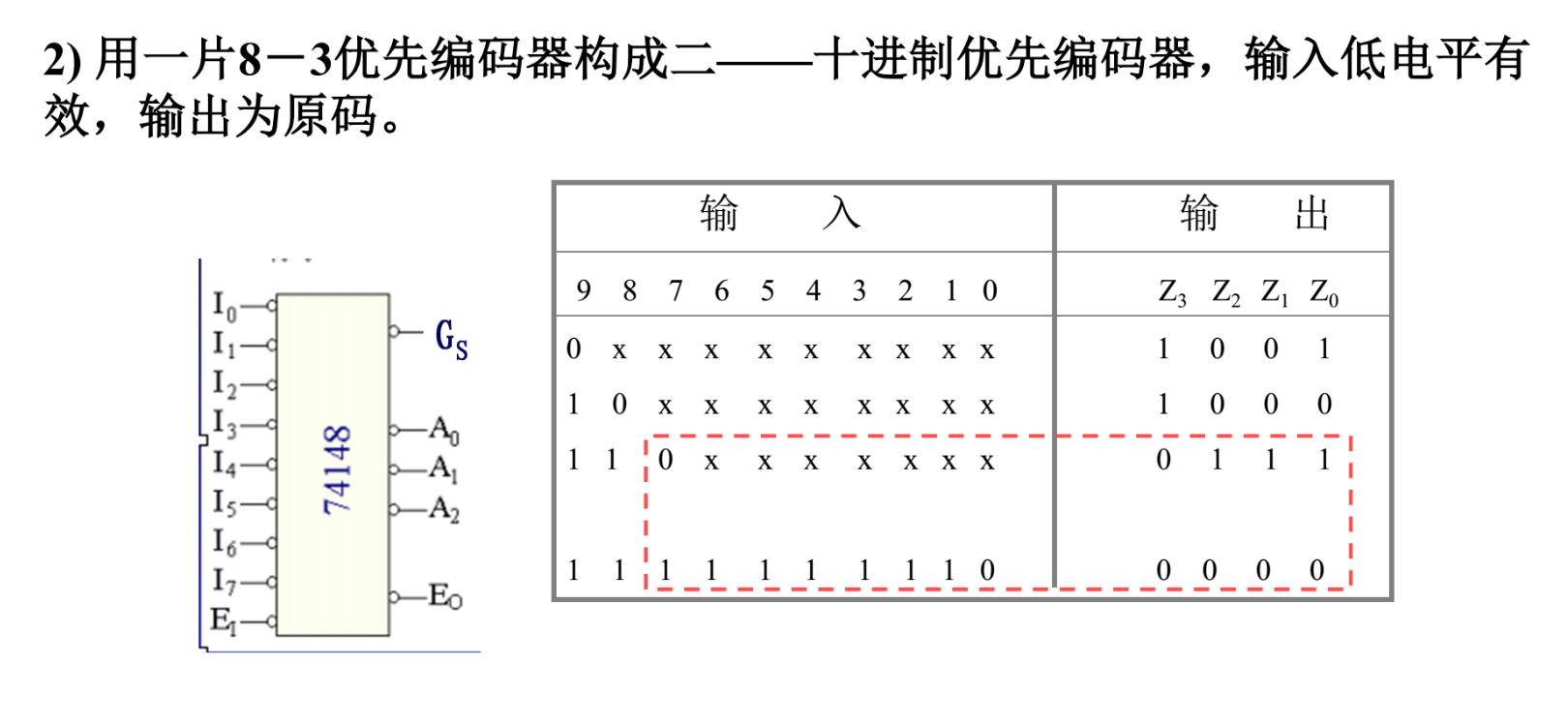
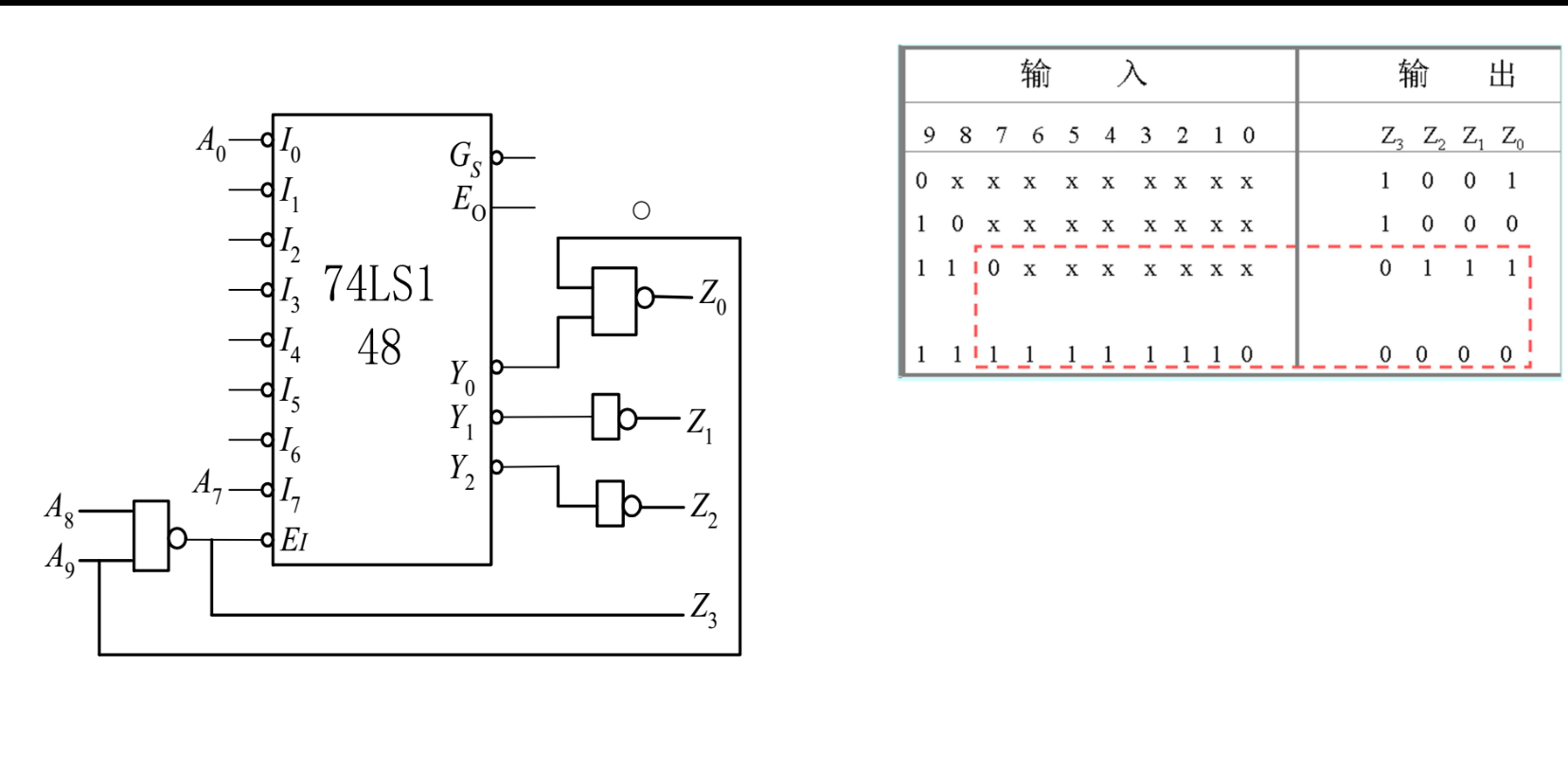
编码器总结

数值比较器

总结

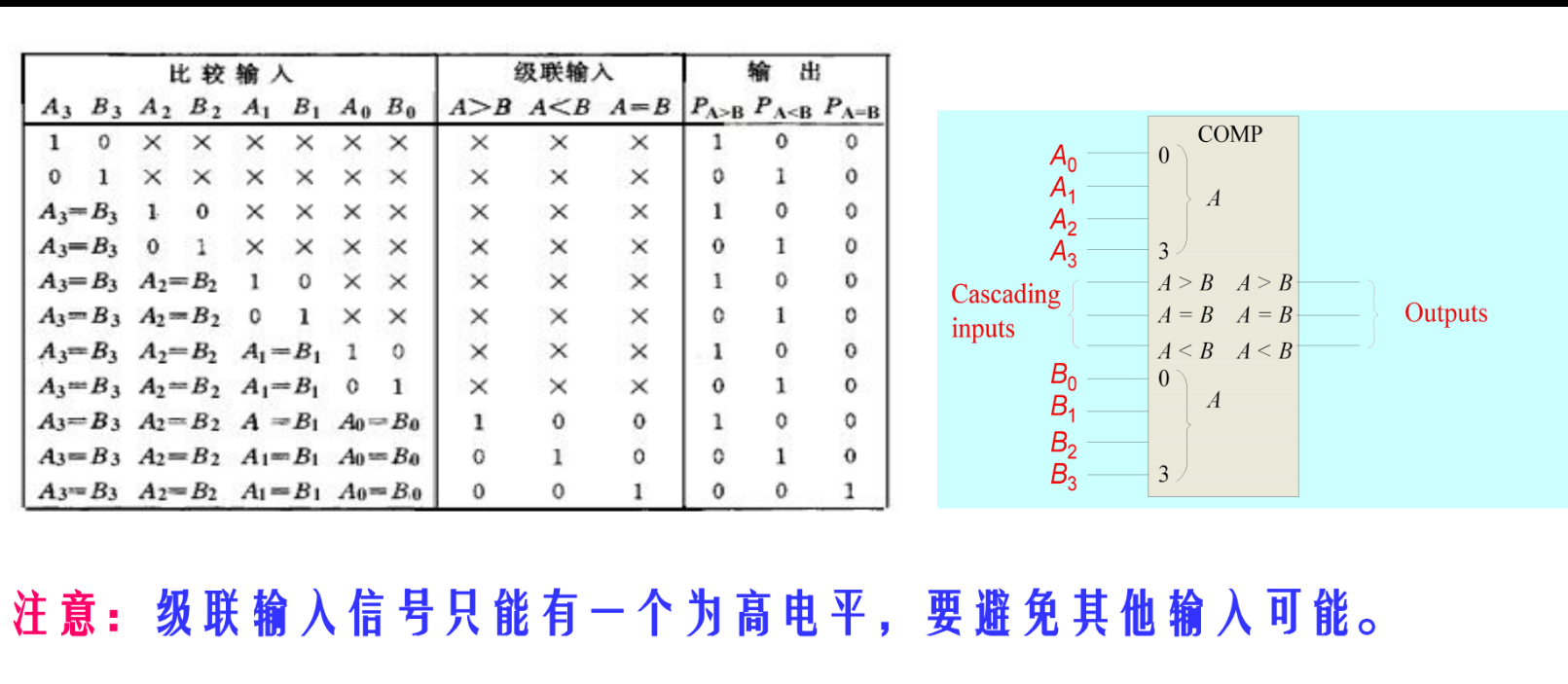
级联输入只能有一个有为有效电平1 最高4位最后比较 （可以理解为优先级），多级比较，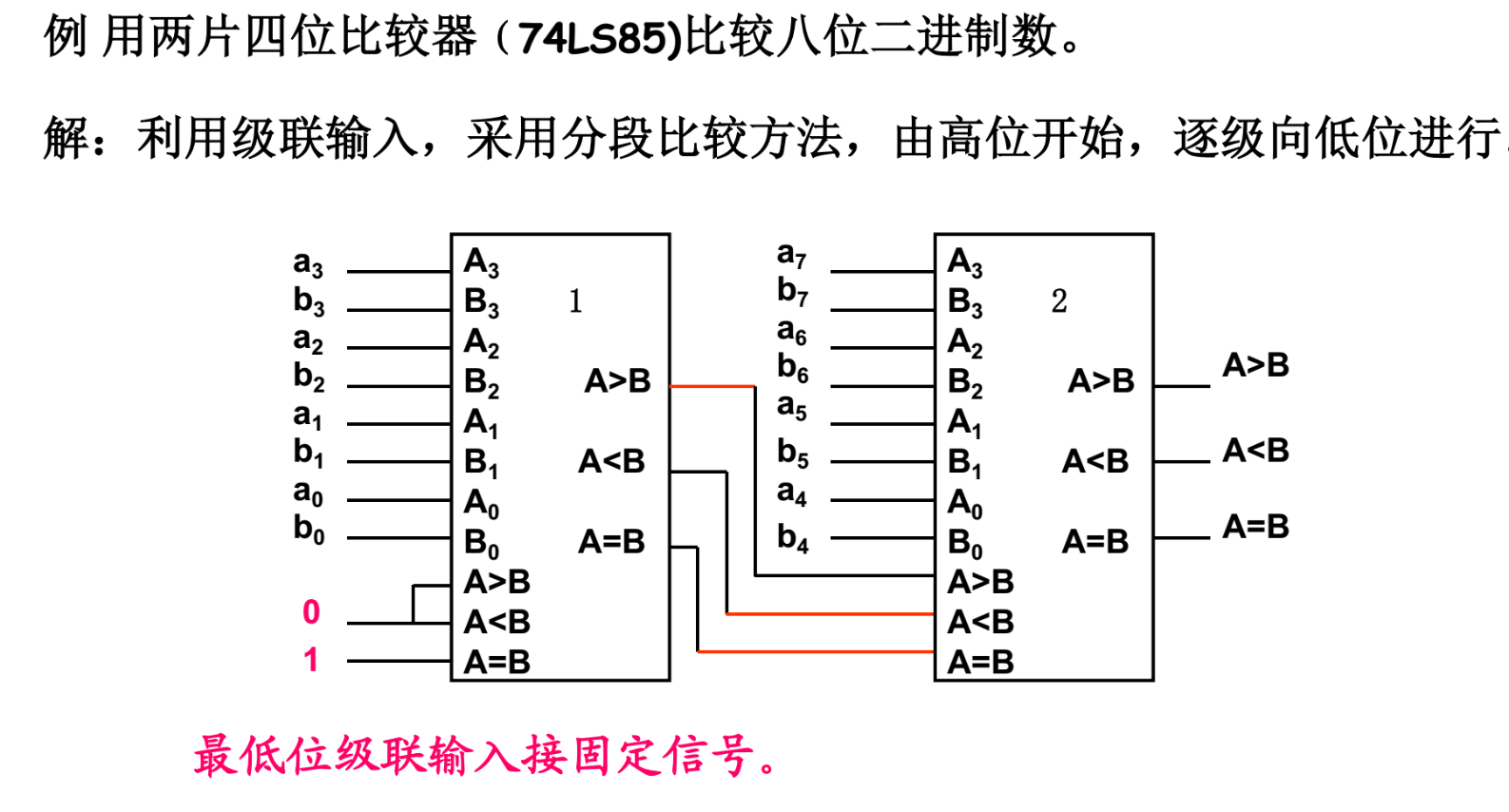

加法器

题型

串行，并行，超前，

减法器（乘法器）

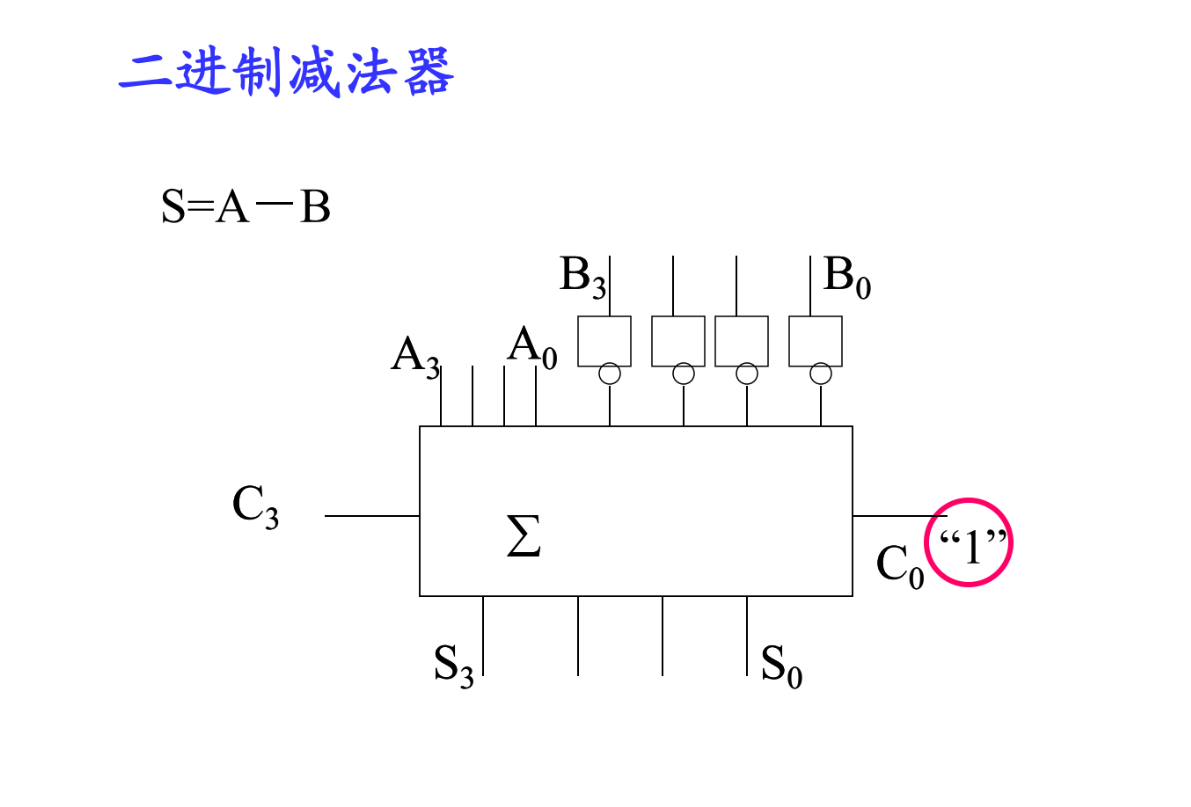
应用（例题）

实现8421码的二进制加法

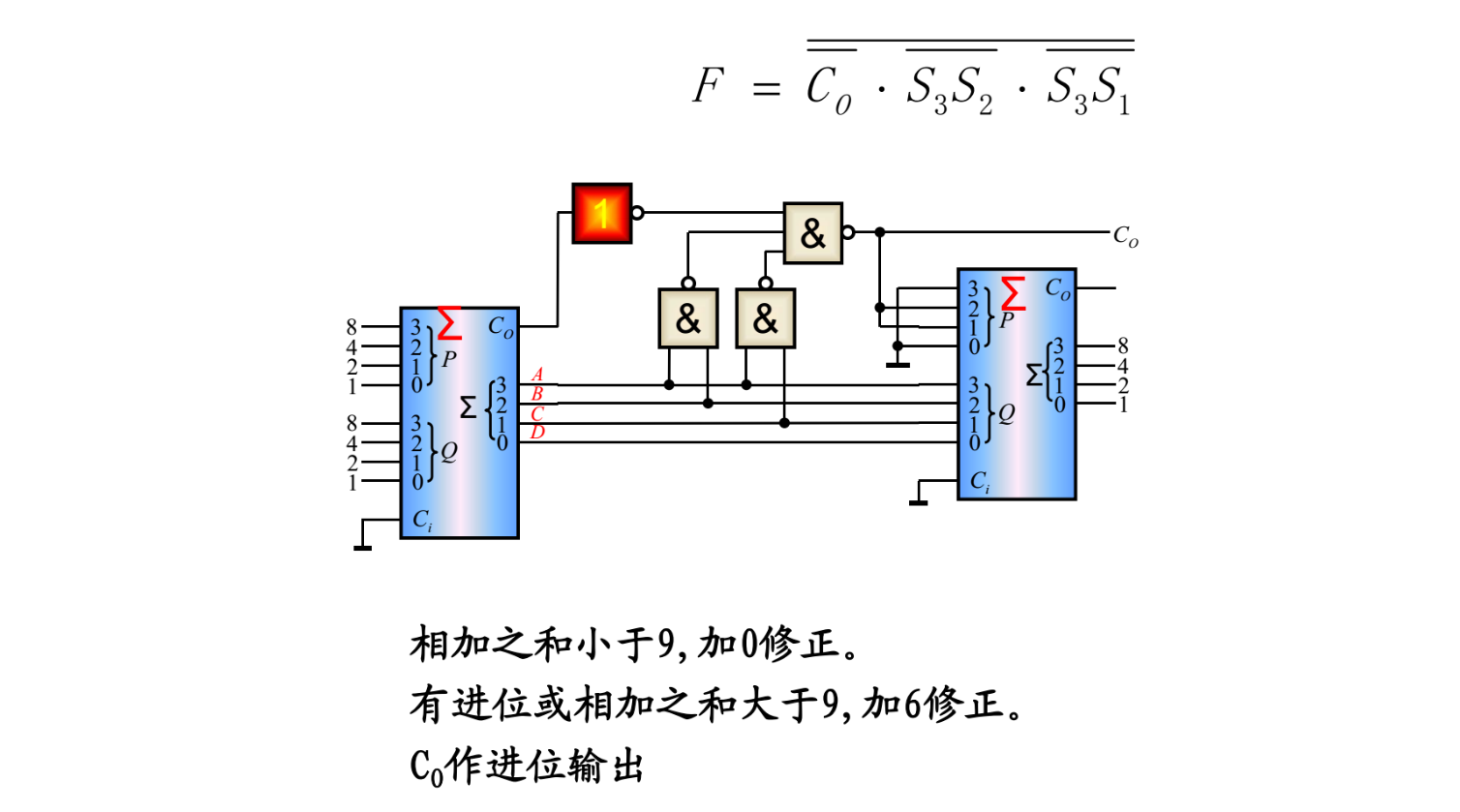
奇偶校验器

74LS280基本功能：

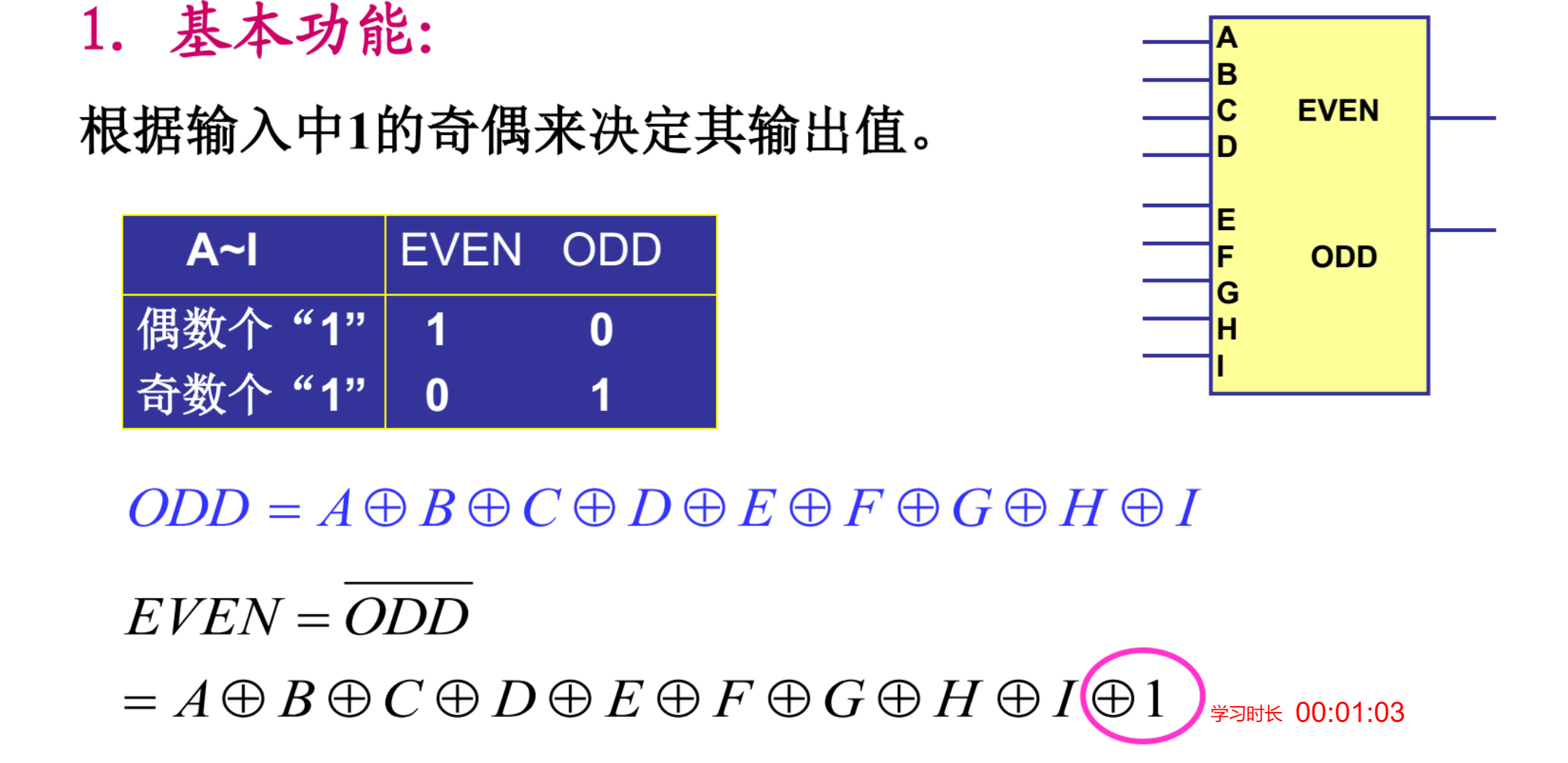
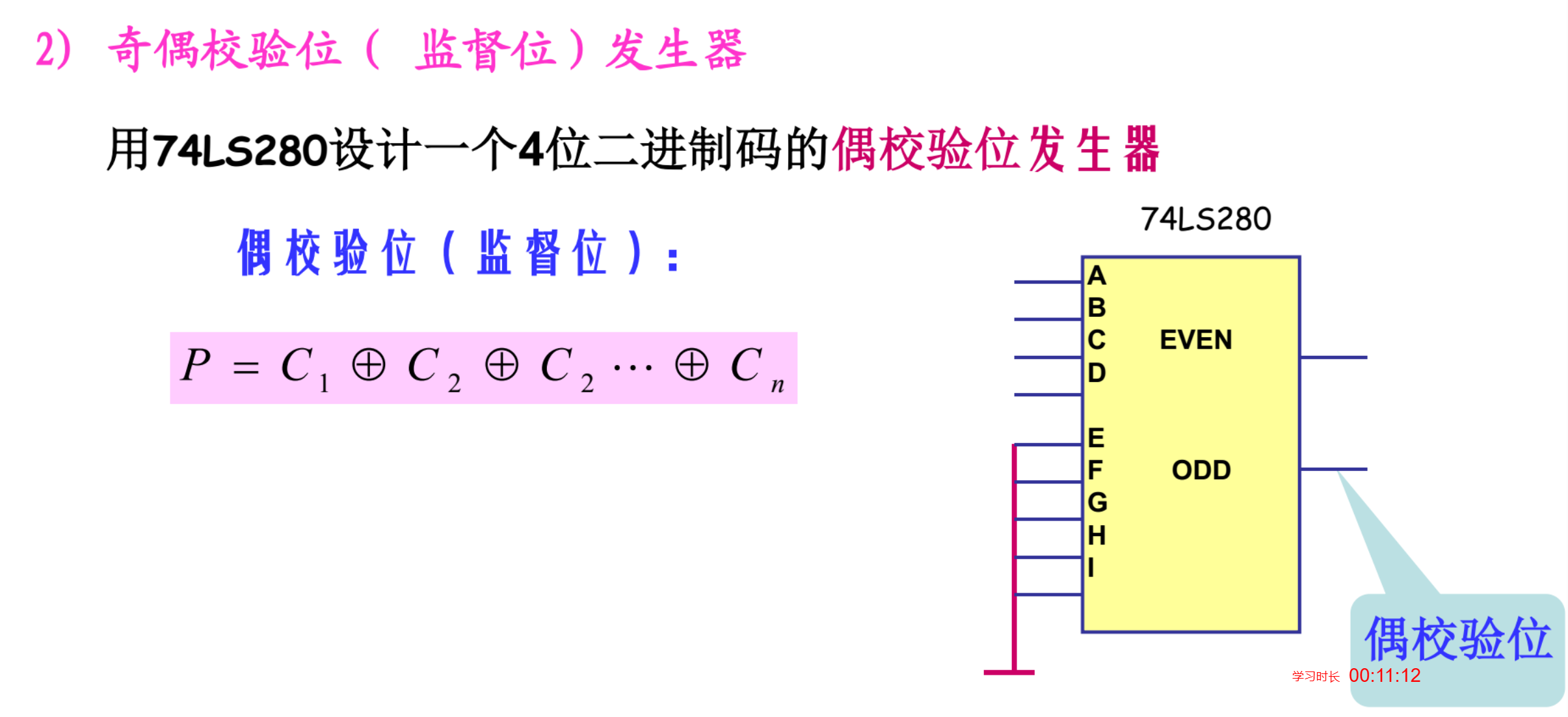
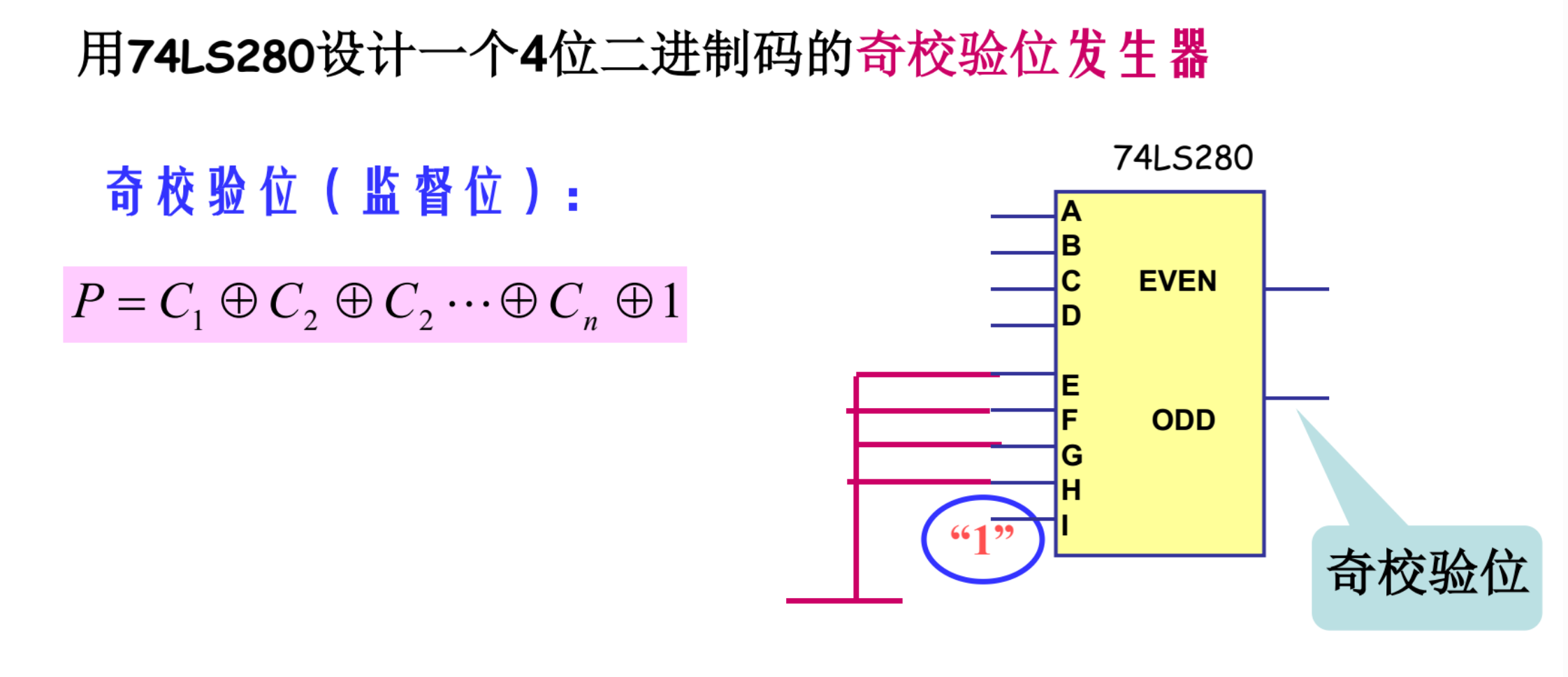
竞争冒险

分类：逻辑冒险和竞争冒险（点击查看具体内容）

检查竞争冒险的常用方法：

逻辑表达式化简法：故对于输出端的逻辑函数在一定条件下能化简成：
Y=A+A’ ， 存在 “0” 型竞争；
** Y=AA’** ，存在 “1” 型竞争；
的情况下，则判定一定有竞争冒险现象。

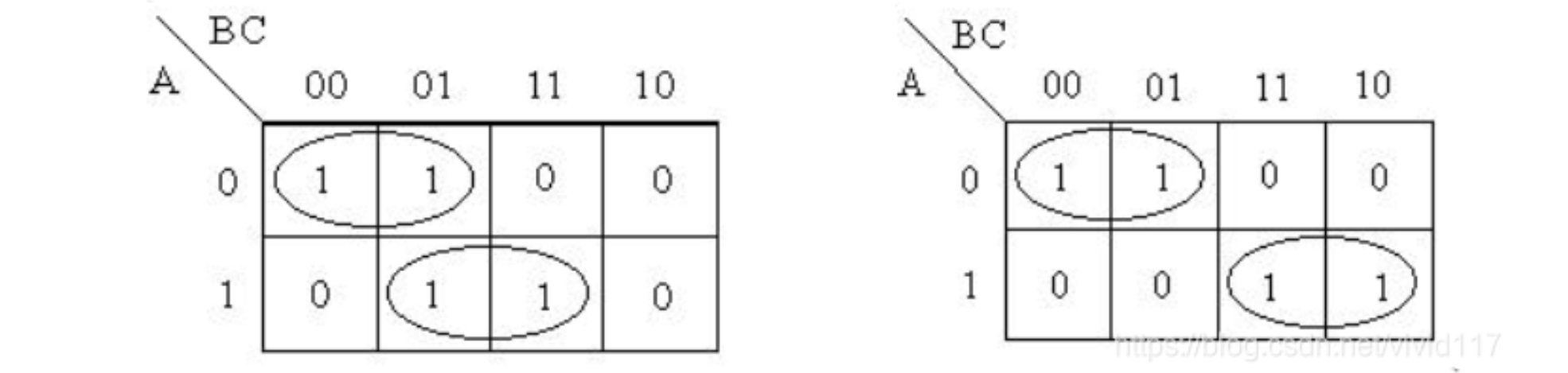
卡洛图法
即如果一个逻辑函数的表达式的卡洛图中所画圈没有重叠并且相切，则判定有竞争冒险。（本质上还是利用上面的方法，只是比较直观形象的判断）
对于以下卡洛图，左图存在竞争冒险，而右边图不存在竞争冒险

第三章时序逻辑

第一节 触发器

​

\[ RS触发器： Q_{n+1}=S+\overline{R}Q_{n}（低电平有效)\\ ------->Q_{n+1}=\overline{S}+RQ_{n}(高电平有效)\\ --------------00是不定状态，如果下一级输入为11，则会出现混乱\\\\ JK触发器：Q_{n+1}=J\overline{Q_n}+\overline{K}Q_n\\\\ D触发器:Q_{n+1}=D\\ T触发器:Q_{n+1}=T\overline{Q_n}+\overline{T}Q_n \]

计算机系统与基础

第零章 cpu的组成结构

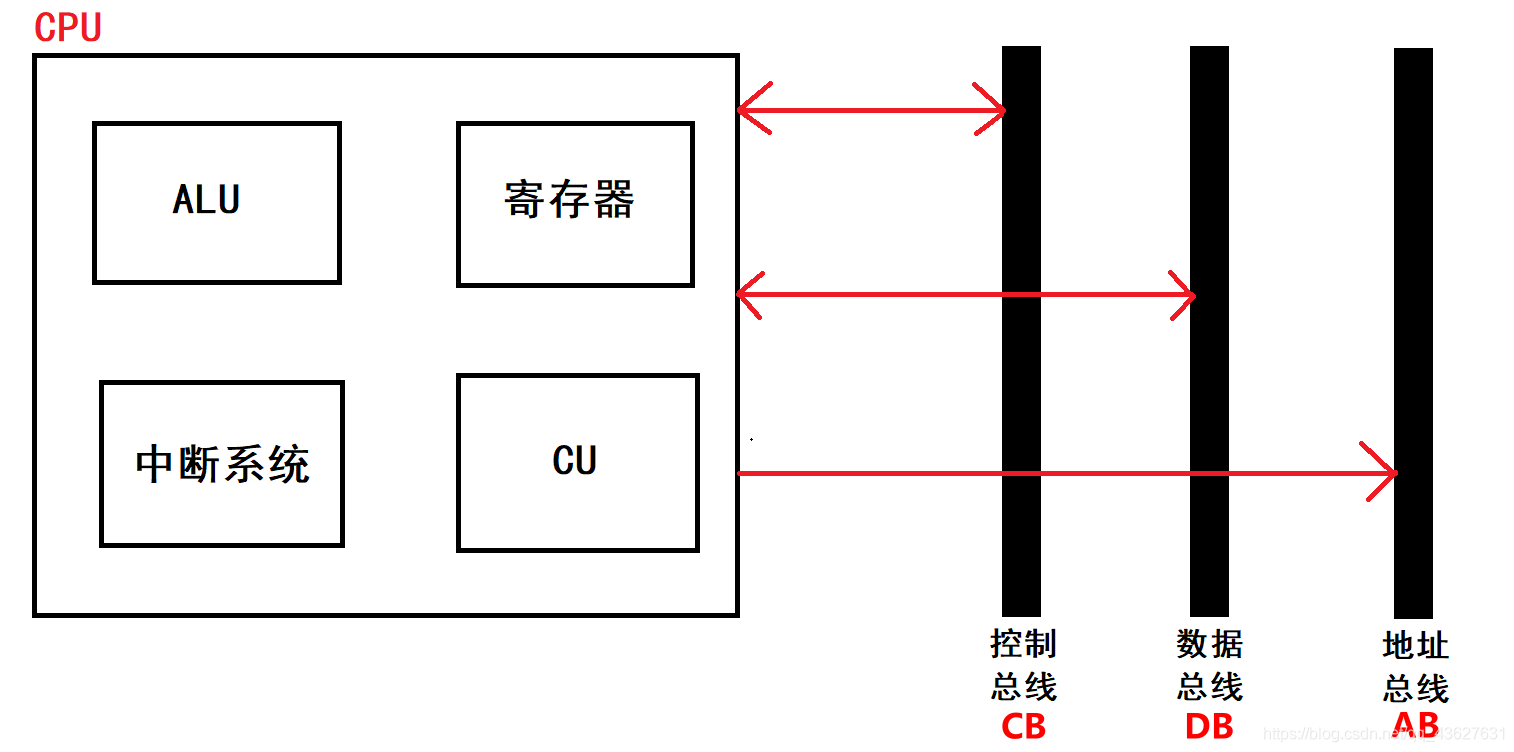
基本组成

CPU内部由ALU（算术逻辑单元）、CU（控制器）、寄存器

（PC、IR、PSW、DR、通用寄存器等）、中断系统组成，外部通过

总线与控制总线、数据总线、地址总线进行相连，对数据和程序进行相关的操作。

第一章数的储存

补码源码转换

补码=~(源码)+1

int 类型最大为 Tmin=0x7fffffff =(1<<31), 最小为 Tmax=0x80000000 =(1<<32)=Tmin+1;

数据类型转换规则

——低转高不会出现错误，高转低会出现精度丢失甚至错误。

double ← ── float 高
↑
long
↑
unsigned
↑
int ← ── char,short 低

第二章汇编语言机器指令

内存单位换算

\[1\mathcal{K}\mathcal{B}= 1024\mathcal{B}={2}^{18}\mathcal{b}\mathcal{i}\mathcal{t} \]

寄存器种类

​ %rsp 栈顶指针（存储的是栈顶地址）

​ %rax 保存函数返回值 ,调用者保护。

​ %rbx %rbp callee saved 被调用者保护

​ %rdi %rsi %rdx %rcx %r8 %r9 按顺序使用共6个储存传递的参数

​ %rip 指令寄存器

leaq地址加载（说白了是一个乘法器） ——leaq （int *p ,%rdx=p, 设p值为x;不局限于地址，也可以用乘法）

​ leaq 7(%rdx ,%rdx,4),%rax = （%rax = 7 + 5*x);

结构体和联合体内存映射

结构体的内每个元素的的起始地址偏移量必须是该类型的整数倍数，对于末端，依然会补齐（由于结构体数组的下一个元素的类型需要补齐）

联合体共享同一储存空间（空间大小取决于最大数据空间)

栈的主要特点

由高地址向低地址生长。

函数的栈帧：当函数执行所需要的储存空间超出寄存器能够存放的大小时候，就会借助栈上的存储空间，这部分空间称为函数的栈帧。

缓冲区溢出

第三章

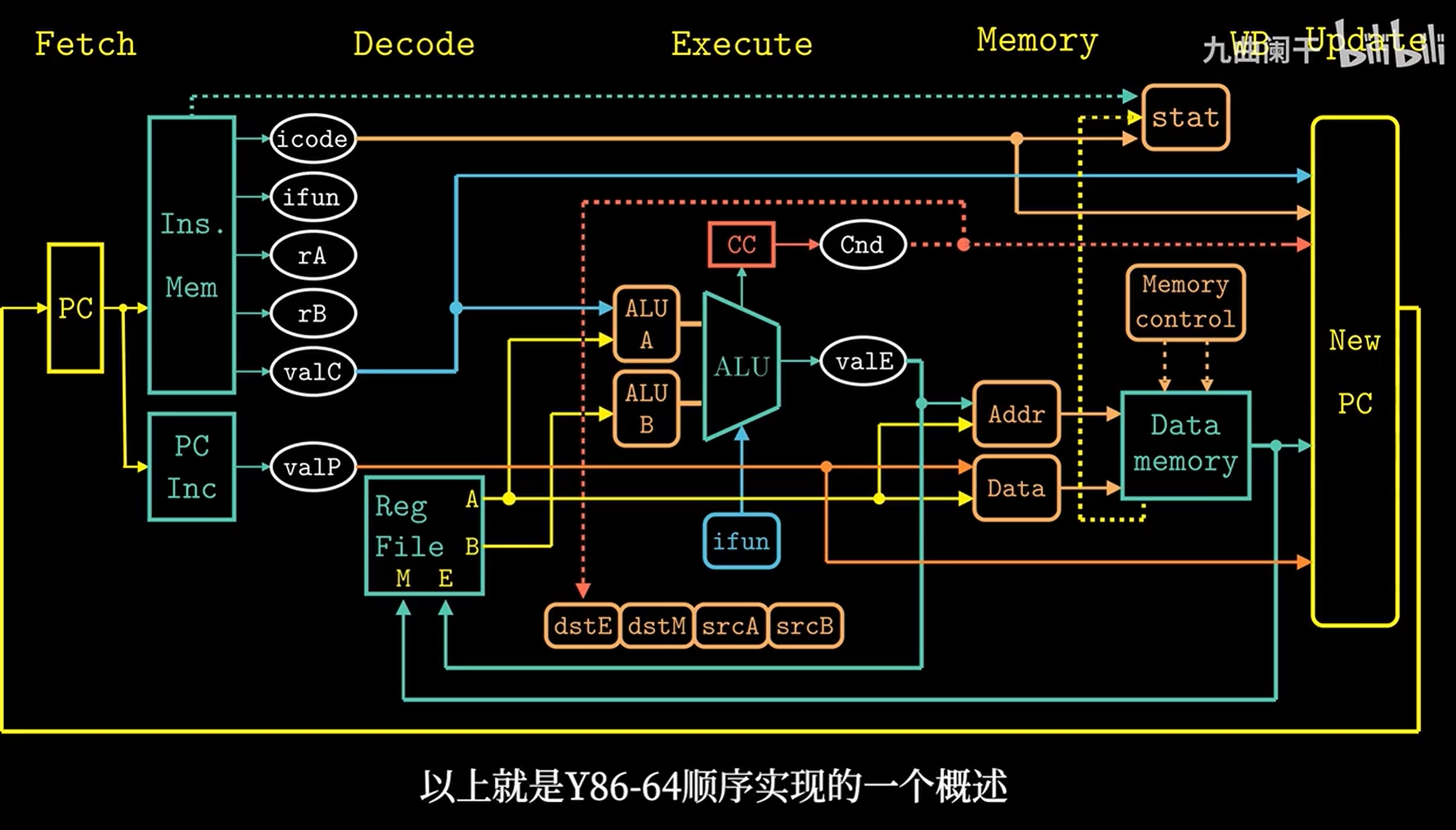
流水线硬件结构

​ 存在错误仅供参考

概率论

第一章

主要内容

全概率公式和贝叶斯公式

比较好的例题

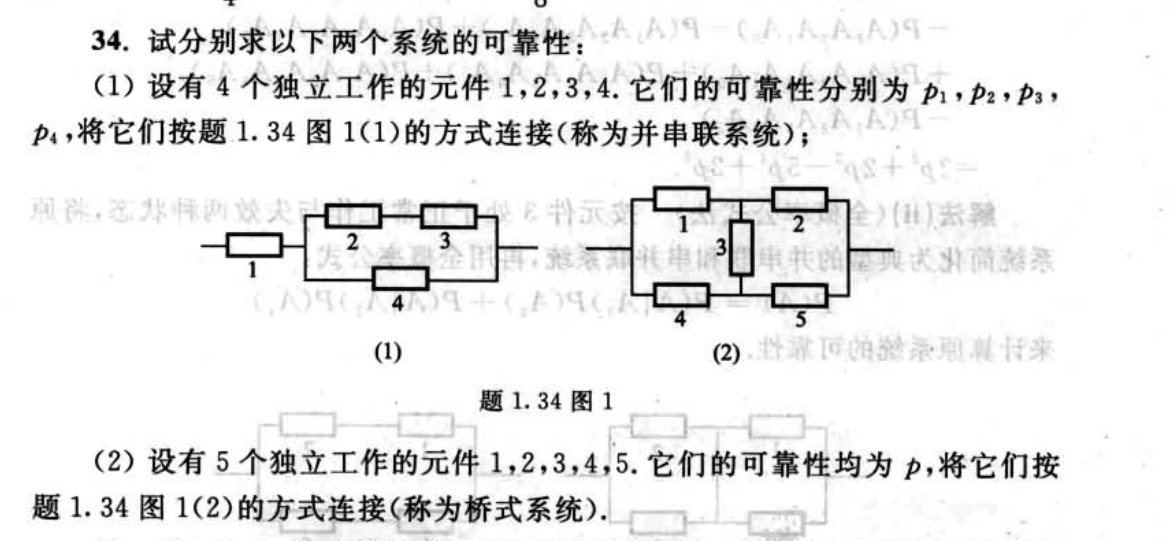
第二章

重点！！！！

​

\[F(x)=P(\text{X} \leqslant x) =\sum_{x_{k} \leqslant x} p_{k} ，\newline由于 X 是取 \leqslant x 的 诸值x_{k} 的概率之和， 故又称是 累积概率函数.\newline 密度函数定义：F(b) - F(a) = \int_{a}^{b} f(x)dx \tag{1} \]

二项分布和泊松分布以及其近似

\[二项分布 X \sim B(n,p)\newline P\{X=k\} = C_n^k p^k q^{n-k}, \;\; k = 0,1,2,...,n\newline 泊松分布：P\{X=k\} = \frac{\lambda ^k}{k!} e^{-\lambda}, \; k = 0,1,2,...\newline 用泊松分布估计二项分布，令n*p=入; \]

指数分布

\[f(x)=\left\{\begin{array}{c} \frac{1}{\theta} e^{-\frac{x}{\theta}}, x>0 \\ 0, x \leq 0 \end{array} \quad(\theta>0)\right. 则称X服从参数为θ的指数分布, 记为X~EXP(θ).\newline F(x)=\left\{\begin{array}{c} 1-e^{-{\theta}{x}}, x\ge 0 \\ 0, x < 0 \end{array} \quad(\theta>0)\right. \newline 指数分布没有记忆性\newline 设X~EXP(θ) ，则对于t, s>0, P\{X>t+s | X>s\} = P\{X>t\} \]

正态分布

\[正态分布：X \sim N(\mu , \sigma ^2)\newline 概率密度：f(x) = \frac{1}{\sqrt{2\pi} \sigma} \cdot e^{- \frac{(x - \mu)^2}{2 \sigma^2}}, - \infty < x < + \infty \]

\[对于分布函数\phi(x)（切记是分布函数！！！）有以下性质\newline \phi (-x)=1-\phi (x) \]

\[标准正态分布：Y = \frac{X - \mu}{\sigma} 可以得到Y \sim N(0,1) \]

\[二维正态分布 (X,Y) \sim N(\mu_1, \mu_2, \sigma_1^2, \sigma_2^2, \rho)\newline 概率密度为 \frac{1}{2\pi \sigma_1 \sigma_2 \cdot\sqrt{1-\rho ^2} } \cdot e^{- \frac{1}{2(1-\rho ^2)} \cdot [\frac{(x-\mu_1)^2}{\sigma_1 ^2} - 2\rho \frac{(x-\mu_1)(y-\mu_2)}{\sigma_1 \sigma_2}+\frac{(y-u_2)^2}{\sigma_2^2} ]}, - \infty < x, y < + \infty\newline \]

二维正态分布的性质

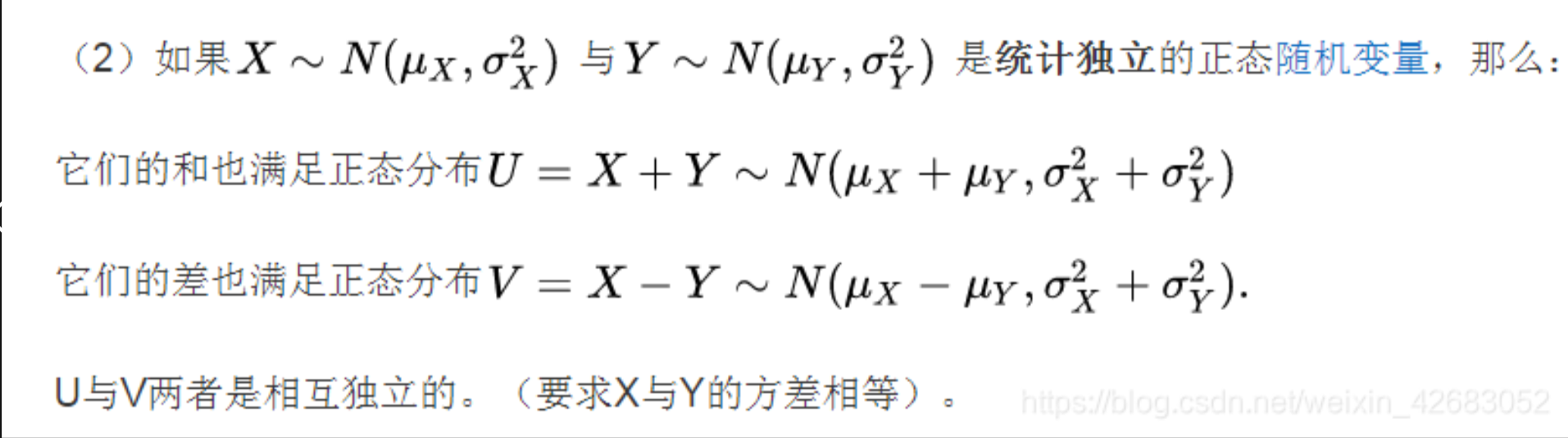
数据结构

第五章数组与广义表

​ 在广义表的表头表尾函数嵌套时，只用留意表头即可

树

基础知识

遍历

前序中序后旭指的是遍历过程中根节点的位置 ，遍历时从根节点开始递归的看

算法如下

void pre_order(TreeNode * Node)//前序遍历递归算法
{
if(Node == NULL)
return;
printf("%d ", Node->data);//显示节点数据，可以更改为其他操作。在前面
pre_order(Node->left);
pre_order(Node->right);
}
void middle_order(TreeNode *Node)//中序遍历递归算法
{
if(Node == NULL)
return;
middle_order(Node->left);
printf("%d ", Node->data);//在中间
middle_order(Node->right);
}
void post_order(TreeNode *Node)//后序遍历递归算法
{
if(Node == NULL)
return;
post_order(Node->left);
post_order(Node->right);
printf("%d ", Node->data);//在最后
}

前序中序后序遍历已知其中两种遍历，求第三个遍历

具体求法control+点击 求法链接

节点和度

​ 所有节点的度数之和+1=总节点数

​ 对于二叉树： 叶节点数=节点数（度为2的节点）+1；

​ 完全二叉树： 节点总数=2*叶节点树+（1或者2）;

路径长度

1. 路径：在一棵树中，从一个结点到另一个结点所经过的所有结点，被我们称为两个结点之间的路径
2. 路径长度：在一棵树中，从一个结点到另一个结点所经过的“边”的数量，被我们称为两个结点之间的路径长度。
3. 结点的带权路径长度：树的根结点到该结点的路径长度和该结点权重的乘积
4. 树的带权路径长度：在一棵树中，所有叶子结点的带权路径长度之和，被称为树的带权路径长度，也被简称为WPL。

​

平衡树专题

推荐的学习视频链接 教学视频一 教学视频二（二叉平衡树的调整）