跳表 skip list

有n个节点的有序链表

每间隔1个节点创建一个节点副本，做索引层，在索引层中，第一个节点指向第二个（等于下一层的第三个），并且添加额外down指针，指向下一层相同的节点

上层在下层之上，数量 = n/2

在上层 n/4 .... n/2^k

k=层数

时间复杂度：

最上层有2个节点

n/2^k = 2

k=log2(n) - 1

算上第一层,总共有 log2(n) 层

每层最多访问3次所以时间复杂度 O(3 * log2(n)) = O(logn)

这和在数组中使用二分查找几乎一样快。但代价是需要使用多一些空间

空间复杂度

第一层需要n个节点

第二层需要 n/2

第三层需要 n/2^2

...

第k层需要 n/2^k

k=log2(n)-1

n+n/2 + n/4 +...n/2^k

根据等比数列求和公式 Sn = ( a1 * (1 - q^n) ) / (1 - q) , q = 1/2

= n * ( 1 - 1/2^n ) / 1/2

= n -2

所以空间杂度是 n

推广到间隔 S 个节点时，情况会怎样

层数

推广到跳表间隔S 个节点后建立一个索引节点

S=3 时，第一层 n, 第二层 n/3, 第三层 n/9 ... 第k层 n/3^k , 最顶层2个节点起建， n/3^k=2 ,k=log3(n/2) = log3(n) - log3(2)

S=4 时，第一层 n, 第二层 n/4, 第三层 n/16 ... 第k层 n/4^k , 最顶层2个节点起建， n/4^k=2 ,k=log4(n/2) = log4(n) - log4(2)

S 时，第一层 n, 第二层 n/s, 第三层 n/s^2 ... 第k层 n/s^k , 最顶层2个节点起建， n/s^k=2 ,k=logs(n/2) = logs(n) - logs(2)

再加上最底层总共有 logs(n) - logs(2) + 1 层

空间

S=3 时，第一层 n, 第二层 n/3, 第三层 n/9 ... 第k层 n/3^k, = 方便计算，排除第一层n个节点，最上层算1个节点 n/3 + n/3^2 +... n/3^(k-3) + 9 + 3 + 1 , Sn = n * ( 1/3 + 1/9 +... 1/3^k) = n/（s-1）

n/（s-1）

时间

S=2 时 O(m*log2(n)) ， m 最多为 3

S=3 时O(m*log3(n) - log3(2) + S) ，忽略掉最后的 log3(2) （S越大，最后的此项越趋近于0，但是算上第一层时，最坏情况还需要走S个元素才可遍历完这当前的一小段） = O(3 * log3(n) + 3)

S 时， O(3 * logS(n) + S）

= O(logS(n))

= O(logn)

个人觉得，跳表有点B树的感觉（上面一级索引，就像一个父节点，需要查找的节点在一个区间中，然后进入到子层查找。）

import java.util.Random;
import java.util.Scanner;

public class SkipList {
    static final int MAX_LEVEL = 16;
    Random r = new Random();
    int count = 0;
    Node dummy;

    public SkipList() {
        dummy = new Node();
    }

    //字符串，引用，数组 内存消耗
    public static class Node {                                  //对象头16字节 + 引用8字节 + 4/8字节填充(机器字长)
        int maxLevel = 0;
        Node[] next = new Node[MAX_LEVEL]; //16+4+4+4 + 8*N   =  28 + 8N  = 28+128
        int key = -1;
        Object data;

        public Node() {
        }

        public Node(int maxLevel, int key, Object data) {
            this.maxLevel = maxLevel;
            this.key = key;
            this.data = data;
        }

        @Override
        public String toString() {
            String s1 = "{" +
                    "key=" + key +
                    ", maxLevel=" + maxLevel +
                    ", next=[";
            int i = 0;
            for (Node o : next) {
                s1 += (o == null ? "n\t" : o.key + "\t");
                if (i == maxLevel)
                    s1 += "|";
                s1 += "\t";
                i++;
            }
            s1 += "]}";
            return s1;
        }
    }

    public Node find(int key) {
        Node cur = dummy;
        int lv = cur.maxLevel;
        System.out.println("find key=" + key);
        while (lv >= 0) {
            System.out.println("find now :" + cur + " lv : " + lv);
            if (cur.next[lv] == null || cur.next[lv].key > key) {
                lv--;                                           //down
                System.out.println("down     :" + (lv > 0 ? "" + cur.next[lv] : lv));
            } else if (cur.next[lv].key < key) {
                cur = cur.next[lv];                             //forward
                System.out.println("forward  :" + cur);
            } else {
                System.out.println("equ      :" + cur.next[lv]);
                return cur.next[lv];                            //==
            }
        }
        return null;
    }

    public void insert(int key) {
        int newLevel = randomLevel();
        System.out.println("insert(" + key + ") newLevel " + newLevel);
        System.out.println("insert(" + key + ") dummy.maxLevel " + dummy.maxLevel);
        dummy.maxLevel = newLevel > dummy.maxLevel ? newLevel : dummy.maxLevel;
        int level = dummy.maxLevel < newLevel ? dummy.maxLevel : newLevel;
        System.out.println("insert(" + key + ") level " + level);
        Node cur = dummy;
        Node[] levelLastNodes = new Node[level + 1];

        while (level >= 0) {
            if (cur.next[level] == null || cur.next[level].key > key) {
                levelLastNodes[level] = cur;                    //down
                level--;
            } else if (cur.next[level].key < key) {
                cur = cur.next[level];                          //forward
                levelLastNodes[level] = cur;
            } else {                                            //==
                break;
            }
        }

        Node newNode = new Node(newLevel, key, null);
        for (int lv = 0; lv < levelLastNodes.length; lv++) {
            newNode.next[lv] = levelLastNodes[lv].next[lv];
            levelLastNodes[lv].next[lv] = newNode;
        }
        count++;
    }

    public void del(int key) {
        int level = dummy.maxLevel;
        Node cur = dummy;
        Node[] levelLastNodes = new Node[dummy.maxLevel + 1];   //记录被删除节点的同层前继节点,用于删除时重新链接后续节点
        Node delNode = null;

        while (level >= 0) {                                    //寻找到被删除节点，并记录前继节点
            if (cur.next[level] == null || cur.next[level].key > key) {
                levelLastNodes[level] = cur;                    //down
                level--;
            } else if (cur.next[level].key < key) {
                cur = cur.next[level];                          //forward
                levelLastNodes[level] = cur;
            } else {                                            //==
                levelLastNodes[level] = cur;
                level--;
            }
        }

        if (cur.next[0] != null && cur.next[0].key == key) {
            delNode = cur.next[0];
            for (int lv = 0; lv < levelLastNodes.length; lv++) { //log
                System.out.println("levelLastNodes " + lv + "\t:" + levelLastNodes[lv]);
            }
            for (int lv = delNode.maxLevel; lv >= 0; lv--) {     //del node
                levelLastNodes[lv].next[lv] = delNode.next[lv];  //使用前继节点后接被删节点的后继节点
                if (levelLastNodes[lv] == dummy && dummy.next[lv] == null) {
                    dummy.maxLevel--;                            //当删除的是在最高层有索引的唯一节点,那么降低全局最大高度
                }
            }
            count--;
        }
        System.out.println("del\t\t:" + delNode);
    }

    public int getCount() {
        return count;
    }

    @Override
    public String toString() {
        StringBuilder sb = new StringBuilder();
        Node n = dummy;
        while (n != null) {
            sb.append(n);
            sb.append('\n');
            n = n.next[0];
        }
        return sb.toString();
    }

    //50% 1层，25% 2层 ， 12.5% 3层 ...
    //next,next/2,next/4,... 最高16层  next/2^16 = next/65536
    protected int randomLevel() {
        int l = 0;
        while (r.nextBoolean() && l < MAX_LEVEL) {
            l++;
        }
        return l;
    }

    public static void main(String args[]) {
        SkipList sl = new SkipList();
        for (int i = 1; i <= 9; i++)                //插入10，20，30.。。90
            sl.insert(i * 10);
        System.out.println(sl.toString());

        System.out.println(sl.find(90));
        System.out.println();
        System.out.println(sl.find(91));
        System.out.println();

        sl.del(9999);
        System.out.println(sl.toString());
        System.out.println();

        Scanner scanner = new Scanner(System.in);
        do {
            System.out.println("Please input action(1=insert,2=del,3=find,0=quit): ");
            int action = scanner.nextInt();
            if (action == 0)
                break;
            System.out.println("Please input key to del:(0 to quit) ");
            int key = scanner.nextInt();

            switch (action) {
                case 1:
                    sl.insert(key);
                    break;
                case 2:
                    sl.del(key);
                    break;
                case 3:
                    System.out.println(sl.find(key));
                    break;
                default:
                    break;
            }
            System.out.println(sl.toString());
            System.out.println();
        } while (true);
    }

}

输出

{key=-1, maxLevel=4, next=[10        10        10        40        40    |    n        n        n        n        n        n        n        n        n        n        n        ]}
{key=10, maxLevel=2, next=[20        20        40    |    n        n        n        n        n        n        n        n        n        n        n        n        n        ]}
{key=20, maxLevel=1, next=[30        30    |    n        n        n        n        n        n        n        n        n        n        n        n        n        n        ]}
{key=30, maxLevel=1, next=[40        40    |    n        n        n        n        n        n        n        n        n        n        n        n        n        n        ]}
{key=40, maxLevel=4, next=[50        50        n        n        n    |    n        n        n        n        n        n        n        n        n        n        n        ]}
{key=50, maxLevel=1, next=[n        n    |    n        n        n        n        n        n        n        n        n        n        n        n        n        n        ]}

find key=40
find now :{key=-1, maxLevel=4, next=[10        10        10        40        40    |    n        n        n        n        n        n        n        n        n        n        n        ]} lv : 4
equ      :{key=40, maxLevel=4, next=[50        50        n        n        n    |    n        n        n        n        n        n        n        n        n        n        n        ]}
{key=40, maxLevel=4, next=[50        50        n        n        n    |    n        n        n        n        n        n        n        n        n        n        n        ]}

find key=41
find now :{key=-1, maxLevel=4, next=[10        10        10        40        40    |    n        n        n        n        n        n        n        n        n        n        n        ]} lv : 4
forward  :{key=40, maxLevel=4, next=[50        50        n        n        n    |    n        n        n        n        n        n        n        n        n        n        n        ]}
find now :{key=40, maxLevel=4, next=[50        50        n        n        n    |    n        n        n        n        n        n        n        n        n        n        n        ]} lv : 4
down     :null
find now :{key=40, maxLevel=4, next=[50        50        n        n        n    |    n        n        n        n        n        n        n        n        n        n        n        ]} lv : 3
down     :null
find now :{key=40, maxLevel=4, next=[50        50        n        n        n    |    n        n        n        n        n        n        n        n        n        n        n        ]} lv : 2
down     :{key=50, maxLevel=1, next=[n        n    |    n        n        n        n        n        n        n        n        n        n        n        n        n        n        ]}
find now :{key=40, maxLevel=4, next=[50        50        n        n        n    |    n        n        n        n        n        n        n        n        n        n        n        ]} lv : 1
down     :0
find now :{key=40, maxLevel=4, next=[50        50        n        n        n    |    n        n        n        n        n        n        n        n        n        n        n        ]} lv : 0
down     :-1
null

del        :null
{key=-1, maxLevel=4, next=[10        10        10        40        40    |    n        n        n        n        n        n        n        n        n        n        n        ]}
{key=10, maxLevel=2, next=[20        20        40    |    n        n        n        n        n        n        n        n        n        n        n        n        n        ]}
{key=20, maxLevel=1, next=[30        30    |    n        n        n        n        n        n        n        n        n        n        n        n        n        n        ]}
{key=30, maxLevel=1, next=[40        40    |    n        n        n        n        n        n        n        n        n        n        n        n        n        n        ]}
{key=40, maxLevel=4, next=[50        50        n        n        n    |    n        n        n        n        n        n        n        n        n        n        n        ]}
{key=50, maxLevel=1, next=[n        n    |    n        n        n        n        n        n        n        n        n        n        n        n        n        n        ]}

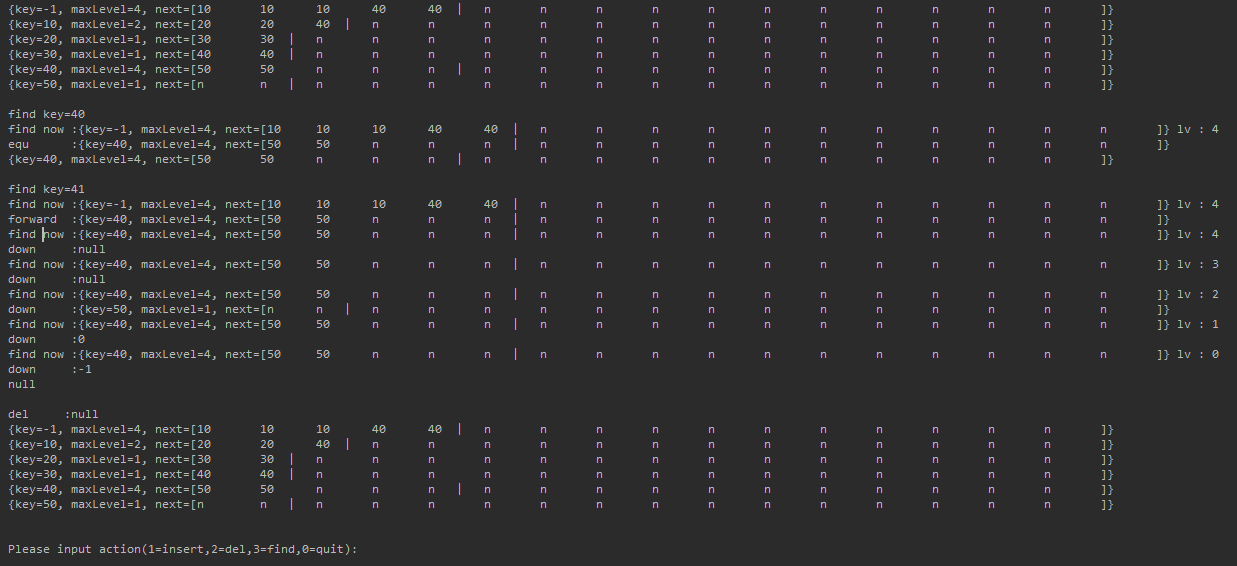
这等宽，等距等\t 字体显示有些问题

下面用截图：

posted on 2019-11-11 02:50 jald 阅读(129) 评论(0) 收藏举报

刷新页面返回顶部

跳表 skip list

导航