ACM寒假集训第七次专题任务
ACM寒假集训第七次专题任务
一、Stockbroker Grapevine
题目:

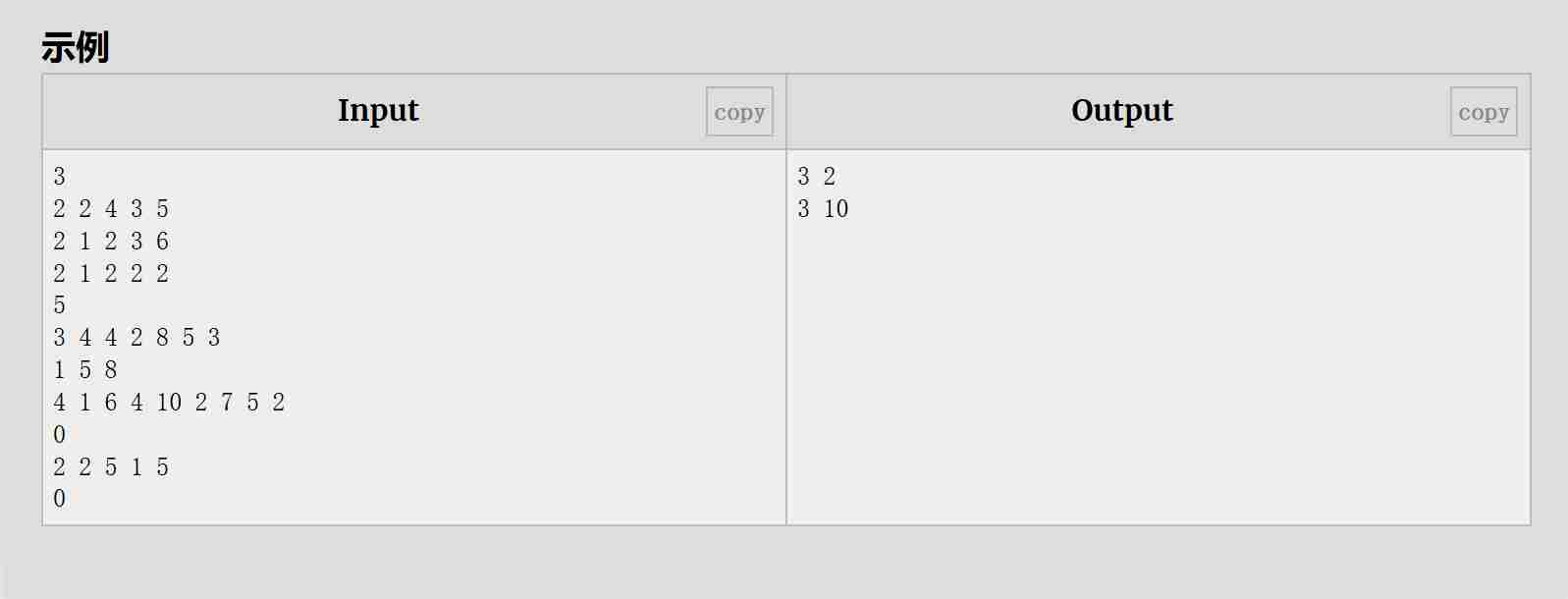
解题思路:
通过 Floyd-Warshall 算法计算所有股票经纪人之间的最短传播时间,从而找到一个最佳起点,使得从该起点传播消息到所有其他经纪人的最长时间最小。如果图是不连通的(即某些经纪人无法通过任何路径联系到),则输出“disjoint”。
AC代码:
#include<iostream>
#include<vector>
#include<algorithm>
using namespace std;
const int maxn=105;
const int inf=0x3f3f3f3f;
int main()
{
while(1)
{
int n;
cin>>n;
if(n==0)
{
break;
}
vector<vector<int>> dist;
dist.resize(n+1);
for(int i=0;i<=n;i++)
{
dist[i].resize(n+1);
}
for(int i=0;i<=n;i++)
{
for(int j=0;j<=n;j++)
{
dist[i][j]=inf;
}
}
for(int i=1;i<=n;i++)
{
dist[i][i]=0;
}
for(int i=1;i<=n;i++)
{
int m;
cin>>m;
while(m--)
{
int to,cost;
cin>>to>>cost;
dist[i][to]=cost;
}
}
for(int k=1;k<=n;k++)
{
for(int i=1;i<=n;i++)
{
for(int j=1;j<=n;j++)
{
if(dist[i][k]!=inf&&dist[k][j]!=inf)
{
dist[i][j]=min(dist[i][j],dist[i][k]+dist[k][j]);
}
}
}
}
int best_start=-1;
int min_max_time=inf;
for(int i=1;i<=n;i++)
{
int max_time=0;
bool all_r=true;
for(int j=1;j<=n;j++)
{
if(dist[i][j]==inf)
{
all_r=false;
break;
}
max_time=max(max_time,dist[i][j]);
}
if(all_r&&max_time<min_max_time)
{
min_max_time=max_time;
best_start=i;
}
}
if(best_start==-1)
{
cout<<"disjoint"<<endl;
}
else
{
cout<<best_start<<" "<<min_max_time<<endl;
}
}
return 0;
}
二、树的直径
题目:
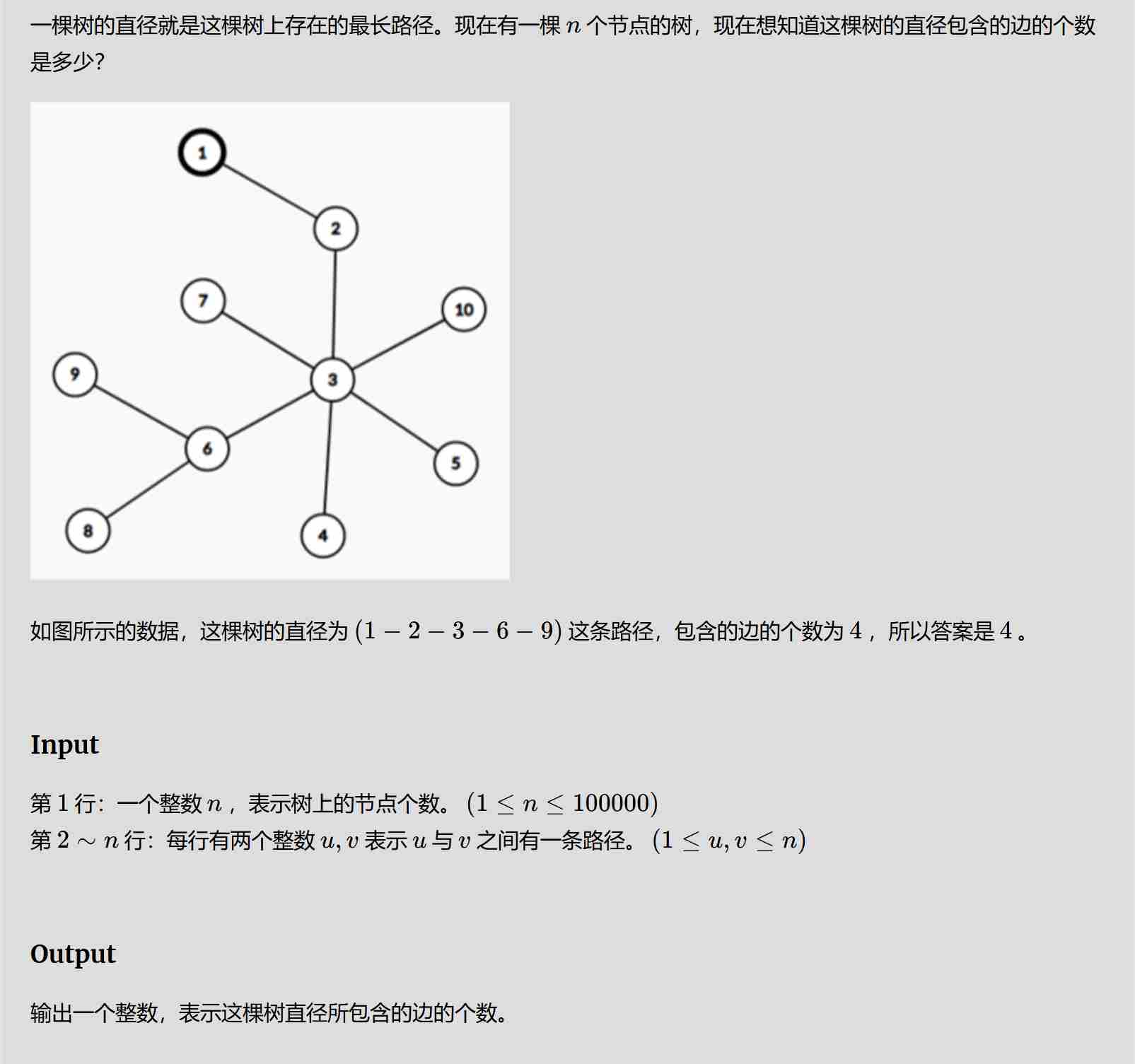
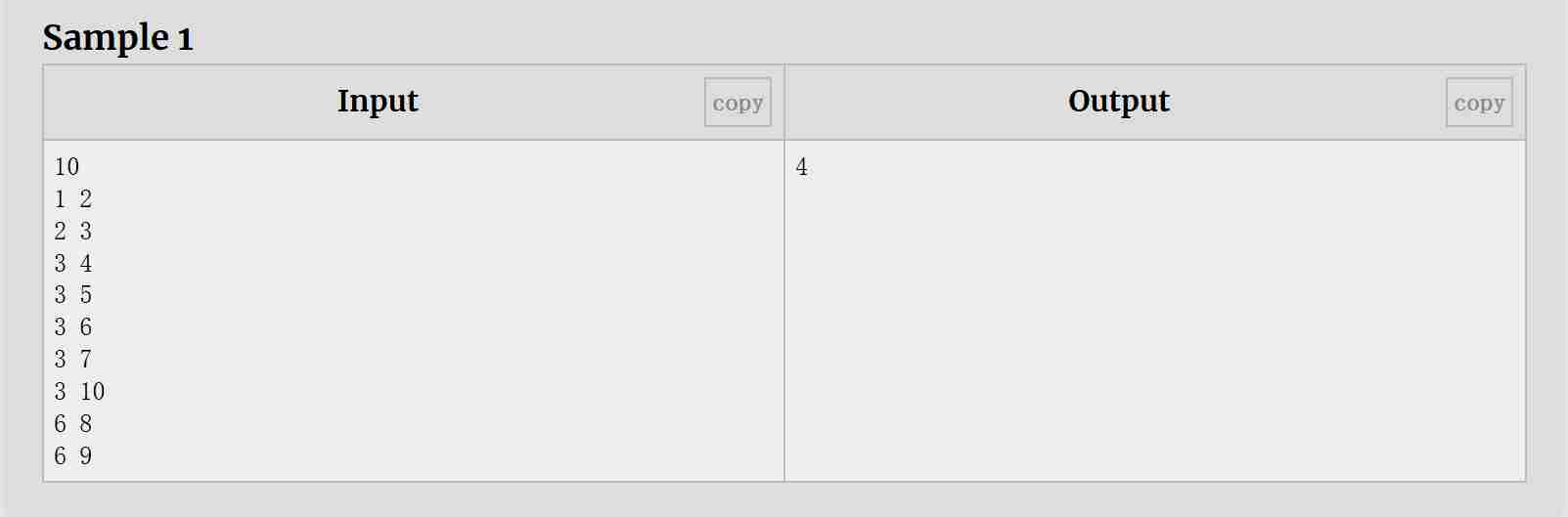
解题思路:
第一次 BFS 从任意节点出发,找到距离最远的节点 A。这个节点 A 一定是直径的一个端点。
第二次 BFS 从 A 出发,找到距离 A 最远的节点 B。节点 A 到 B 的路径即为树的直径。
运用了树的性质:从任意节点出发,最远的节点一定是直径的一个端点。
AC代码:
#include<iostream>
#include<vector>
#include<queue>
using namespace std;
const int maxn=100009;
vector<int> adj[maxn];
int dist[maxn];
bool visited[maxn];
int n;
void bfs(int start,int &farthestnode,int &maxdist)
{
queue<int> q;
q.push(start);
visited[start]=true;
dist[start]=0;
while(!q.empty())
{
int u=q.front();
q.pop();
for(int v:adj[u])
{
if(!visited[v])
{
visited[v]=true;
dist[v]=dist[u]+1;
q.push(v);
}
}
}
maxdist=0;
farthestnode=start;
for(int i=1;i<=n;i++)
{
if(dist[i]>maxdist)
{
maxdist=dist[i];
farthestnode=i;
}
}
}
int main()
{
cin>>n;
for(int i=1;i<n;i++)
{
int u,v;
cin>>u>>v;
adj[u].push_back(v);
adj[v].push_back(u);
}
int farthestnode1,maxdist1;
bfs(1,farthestnode1,maxdist1);
for(int i=1;i<=n;i++)
{
visited[i]=false;
}
int farthestnode2,maxdist2;
bfs(farthestnode1,farthestnode2,maxdist2);
cout<<maxdist2;
return 0;
}
三、Invitation Cards
题目:

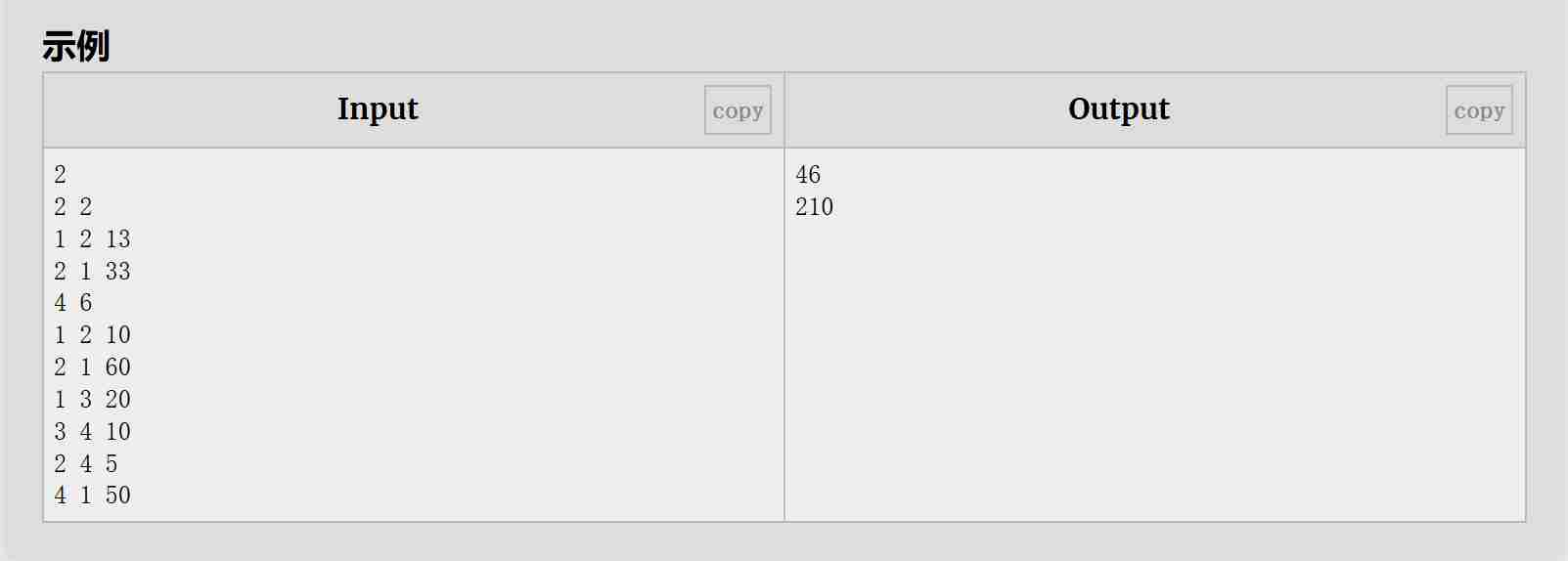
解题思路:
使用邻接表存储正向图(从出发站到目的站)和反向图(从目的站到出发站)。正向图用于计算从CCS到每个站点的最短路径;反向图用于计算从每个站点返回CCS的最短路径。
对于每个测试用例,分别从CCS(站点1)出发,使用Dijkstra算法计算:
distto[i]:从CCS到站点i的最短路径。
distfrom[i]:从站点i返回CCS的最短路径。
对于每个站点i,计算其往返总费用:distto[i] + distfrom[i]。将所有站点的往返费用相加,即为最终的最小交通费用。
AC代码:
#include<iostream>
#include<vector>
#include<queue>
#include<cstring>
#include<algorithm>
#include<functional>
using namespace std;
const int maxn=1000009;
const int inf=0x3f3f3f3f;
struct edge{
int to;
int cost;
};
vector<edge> graph[maxn];
vector<edge> rgraph[maxn];
int distto[maxn];
int distfrom[maxn];
void dijkstra(int start,int dist[],vector<edge> graph[])
{
priority_queue<pair<int,int>,vector<pair<int,int>>,greater<pair<int,int>>> pq;
pq.push({0,start});
dist[start]=0;
while(!pq.empty())
{
int u=pq.top().second;
int d=pq.top().first;
pq.pop();
if(d>dist[u])
{
continue;
}
for(auto &e:graph[u])
{
int v=e.to;
int cost=e.cost;
if(dist[v]>dist[u]+cost)
{
dist[v]=dist[u]+cost;
pq.push({dist[v],v});
}
}
}
}
int main()
{
int N;
cin>>N;
while(N--)
{
int P,Q;
cin>>P>>Q;
for(int i=1;i<=P;i++)
{
graph[i].clear();
rgraph[i].clear();
}
for(int i=0;i<Q;i++)
{
int u,v,cost;
cin>>u>>v>>cost;
graph[u].push_back({v,cost});
rgraph[v].push_back({u,cost});
}
fill(distto+1,distto+P+1,inf);
fill(distfrom+1,distfrom+P+1,inf);
dijkstra(1,distto,graph);
dijkstra(1,distfrom,rgraph);
long long sum=0;
for(int i=2;i<=P;i++)
{
sum+=distto[i]+distfrom[i];
}
cout<<sum<<endl;
}
}
四、战略游戏
题目:

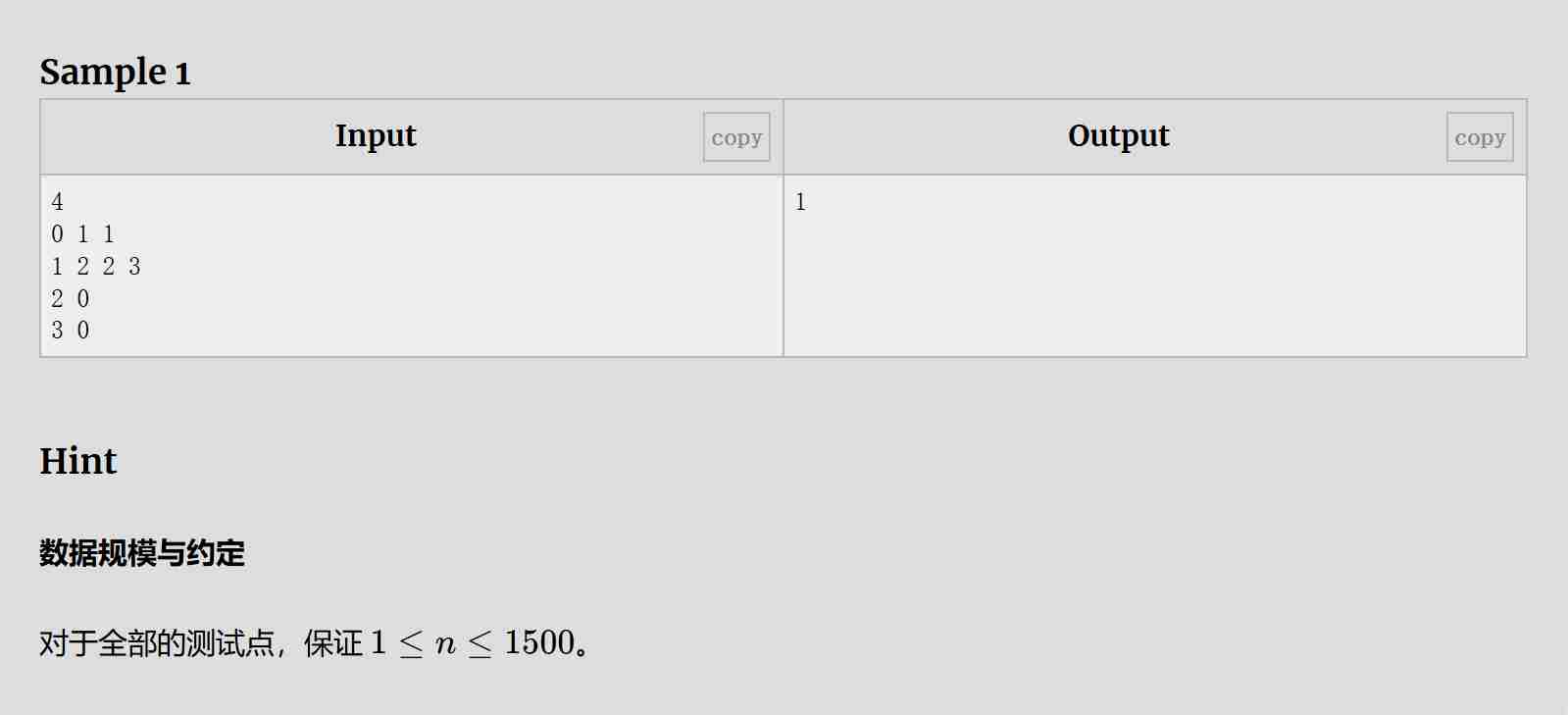
解题思路:
定义 dp[u][0]:表示节点 u 不放置士兵时,覆盖该子树所需的最少士兵数。
定义 dp[u][1]:表示节点 u 放置士兵时,覆盖该子树所需的最少士兵数。
状态转移方程:如果节点 u 不放置士兵(dp[u][0])则至少有一个子节点必须放置士兵;如果节点 u 放置士兵(dp[u][1])则所有子节点可以选择放置或不放置士兵。
使用DFS计算每个节点的两种状态(放置和不放置士兵)。
AC代码:
#include<iostream>
#include<vector>
#include<algorithm>
using namespace std;
const int maxn=1509;
vector<int> tree[maxn];
int dp[maxn][2];
void dfs(int u,int parent)
{
dp[u][0]=0;
dp[u][1]=1;
for(int v:tree[u])
{
if(v==parent)
{
continue;
}
dfs(v,u);
dp[u][0]+=dp[v][1];
dp[u][1]+=min(dp[v][0],dp[v][1]);
}
}
int main()
{
int n;
cin>>n;
for(int i=0;i<n;i++)
{
int id,k;
cin>>id>>k;
while(k--)
{
int r;
cin>>r;
tree[id].push_back(r);
tree[r].push_back(id);
}
}
dfs(0,-1);
cout<<min(dp[0][0],dp[0][1]);
return 0;
}
五、飞行路线
题目:

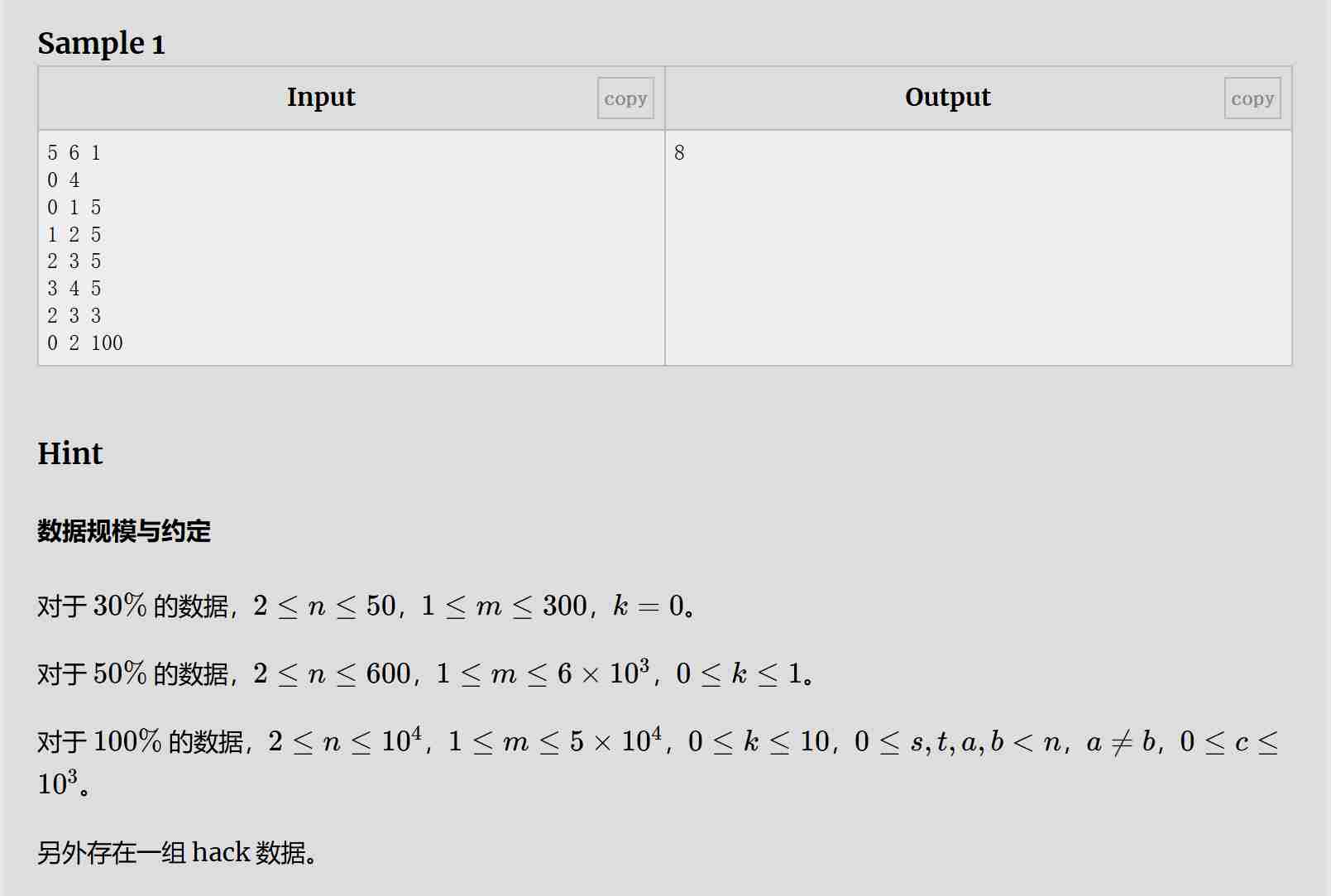
解题思路:
求从起点城市 s 到终点城市 t 的最少花费,但允许在最多 k 次航线上免费乘坐。这意味着:
每次免费乘坐可以节省一次飞行的费用。
免费乘坐次数用完后,后续的飞行需要支付正常费用。
对于每个状态 (u,r,cost),考虑两种转移方式:
- 免费乘坐:如果 r>0,可以选择免费乘坐到相邻节点 v,状态变为 (v,r−1,cost)。
- 付费乘坐:可以选择付费乘坐到相邻节点 v,状态变为 (v,r,cost+c),其中 c 是从 u 到 v 的费用。
AC代码:
#include<iostream>
#include<vector>
#include<queue>
#include<cstring>
#include<algorithm>
using namespace std;
const int maxn=10005;
const int inf=0x3f3f3f3f;
struct edge{
int to;
int cost;
};
vector<edge> graph[maxn];
int dist[maxn][11];
void dijkstra(int s,int t,int k)
{
priority_queue<pair<int,pair<int,int>>,vector<pair<int,pair<int,int>>>,greater<pair<int,pair<int,int>>>> pq;
pq.push({0,{s,k}});
dist[s][k]=0;
while(!pq.empty())
{
int cost=pq.top().first;
int u=pq.top().second.first;
int r=pq.top().second.second;
pq.pop();
if(u==t)
{
continue;
}
for(auto &e:graph[u])
{
int v=e.to;
int c=e.cost;
if(r>0&&dist[v][r-1]>cost)
{
dist[v][r-1]=cost;
pq.push({cost,{v,r-1}});
}
if(dist[v][r]>cost+c)
{
dist[v][r]=cost+c;
pq.push({cost+c,{v,r}});
}
}
}
}
int main()
{
int n,m,k;
cin>>n>>m>>k;
int s,t;
cin>>s>>t;
for(int i=0;i<m;i++)
{
int a,b,c;
cin>>a>>b>>c;
graph[a].push_back({b,c});
graph[b].push_back({a,c});
}
for(int i=0;i<n;i++)
{
for(int j=0;j<=k;j++)
{
dist[i][j]=inf;
}
}
dijkstra(s,t,k);
int minc=inf;
for(int r=0;r<=k;r++)
{
minc=min(minc,dist[t][r]);
}
cout<<minc;
return 0;
}
六、二叉苹果树
题目:

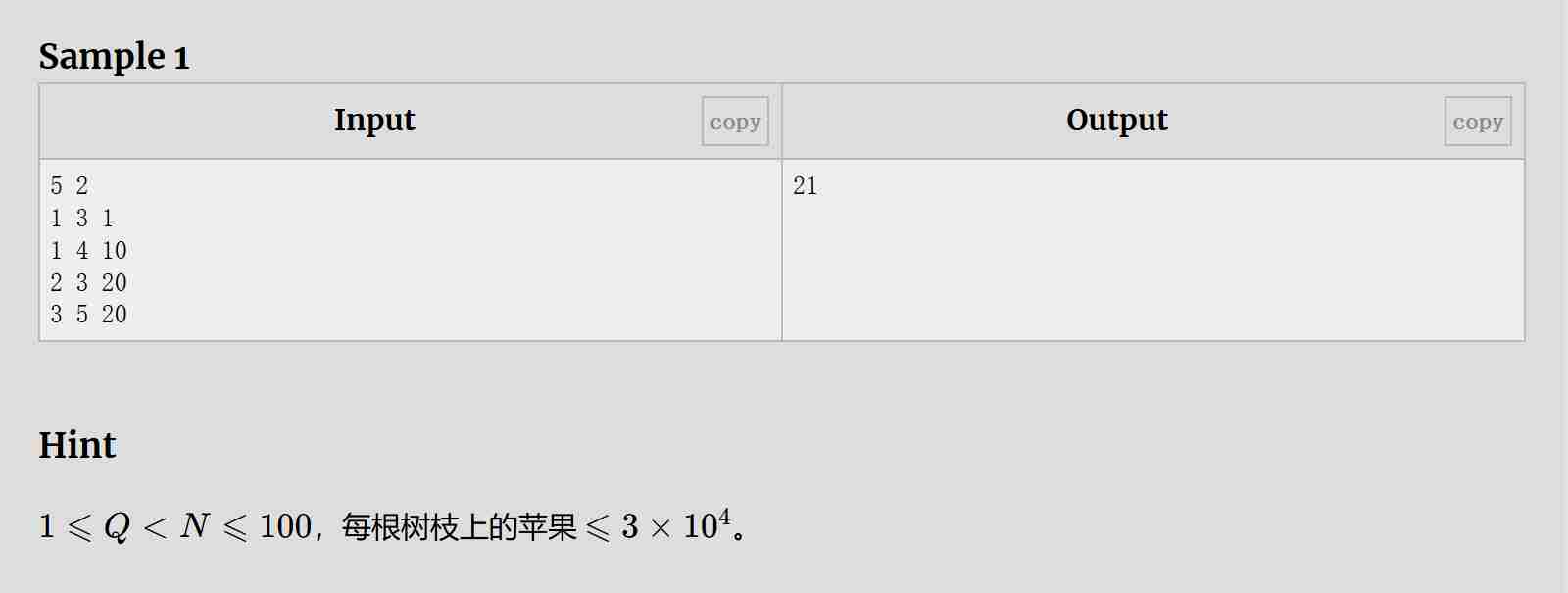
解题思路:
使用邻接表 son 存储每个节点的子节点,二维数组 val 存储每根树枝上的苹果数量。f[x][j] 表示以节点 x 为根,保留 j 根树枝时,最多能保留的苹果数量。
从根节点(节点 1)开始,递归遍历每个节点的子节点。对于每个节点 x,考虑其所有子节点 ny,更新动态规划数组 f。
对于每个节点 x,假设保留 j 根树枝,考虑其子节点 ny:如果保留 k 根树枝在子节点 ny 上,则剩余 j−k−1 根树枝可以分配给其他子节点。更新 f[x][j] 的值,考虑当前子节点 ny 的苹果数量 val[x][ny],以及子节点 ny 的最优解 f[ny][k]。
AC代码:
#include<iostream>
#include<vector>
using namespace std;
vector<int> son[109];
int n,q;
int f[109][109];
int val[109][109];
int used[109];
void dfs(int x)
{
used[x]=1;
for(int i=0;i<son[x].size();i++)
{
int ny=son[x][i];
if(used[ny]==1)
{
continue;
}
used[ny]=1;
dfs(ny);
for(int j=q;j>=1;j--)
{
for(int k=j-1;k>=0;k--)
{
f[x][j]=max(f[x][j],val[x][ny]+f[ny][k]+f[x][j-k-1]);
}
}
}
}
int main()
{
cin>>n>>q;
for(int i=1;i<n;i++)
{
int a,b,c;
cin>>a>>b>>c;
val[a][b]=c;
val[b][a]=c;
son[a].push_back(b);
son[b].push_back(a);
}
dfs(1);
cout<<f[1][q];
return 0;
}
学习总结
一、图与树的基本概念
(一)图(Graph)
- 定义
图是由顶点集合(Vertex Set)和边集合(Edge Set)组成的结构,记作 G=(V,E)。顶点之间通过边相连,边可以是有向的(有向图),也可以是无向的(无向图)。 - 分类
- 无向图:边没有方向,如果顶点 u 和 v 之间有边,则 u 和 v 是相互连通的。
- 有向图:边有方向,从一个顶点指向另一个顶点。如果从 u 到 v 有一条边,但不一定从 v 到 u 有边。
- 带权图:每条边都有一个权重(权值),表示边的“代价”或“距离”。
- 存储方式
- 邻接矩阵:用一个二维数组$ adj[n][n] $表示,其中 n 是顶点数。如果顶点 u 和 v 之间有边,则 \(adj[u][v]=1\)(无权图)或 \(adj[u][v]=weight\)(带权图)。优点是方便判断两点之间是否有边,缺点是空间复杂度高(O(n2))。
- 邻接表:用一个数组存储每个顶点的邻接点列表。对于每个顶点 u,存储所有与 u 直接相连的顶点。优点是空间复杂度低(O(n+m),其中 m 是边数),适合稀疏图。
(二)树(Tree)
- 定义
树是一种特殊的图,它是无向图的连通无环子图。树具有以下性质:- 任意两个顶点之间有且仅有一条路径。
- 如果树有 n 个顶点,则一定有 n−1 条边。
- 分类
- 无根树:没有明确的根节点,任意一个顶点都可以作为根。
- 有根树:有一个明确的根节点,树上的每个顶点都有一个唯一的父节点(根节点除外)。
- 存储方式
- 邻接表:与图的邻接表类似,存储每个节点的子节点。
- 父节点数组:用一个数组 parent[n] 表示每个节点的父节点。
二、图的存储与建图
(一)存储方式
-
邻接矩阵
const int MAXN = 100; // 最大顶点数 int adj[MAXN][MAXN]; // 邻接矩阵初始化:无权图用 0 和 1 表示,带权图用无穷大(如
INT_MAX)表示无边。 -
邻接表
const int MAXN = 100; // 最大顶点数 const int MAXM = 200; // 最大边数 vector<int> adj[MAXN]; // 邻接表或者使用链式前向星存储边:
struct Edge { int to, weight; } edges[MAXM]; int head[MAXN], tot = 0; // head数组存储每个点的头节点,tot是边的编号 void addEdge(int from, int to, int weight) { edges[tot] = {to, weight}; edges[tot].next = head[from]; head[from] = tot++; }
(二)建图
-
无向图
void addEdge(int u, int v, int w) { adj[u][v] = w; adj[v][u] = w; // 无向图需要双向存储 }或者邻接表:
void addEdge(int u, int v) { adj[u].push_back(v); adj[v].push_back(u); // 无向图需要双向存储 } -
有向图
void addEdge(int u, int v, int w) { adj[u][v] = w; }或者邻接表:
void addEdge(int u, int v) { adj[u].push_back(v); }
三、树的遍历
(一)深度优先搜索(DFS)
-
递归实现
void dfs(int u, int parent) { for (int v : adj[u]) { if (v == parent) continue; // 避免回溯 dfs(v, u); } } -
非递归实现(用栈)
stack<int> s; vector<bool> visited(n, false); s.push(root); while (!s.empty()) { int u = s.top(); s.pop(); if (!visited[u]) { visited[u] = true; for (int v : adj[u]) { if (!visited[v]) { s.push(v); } } } }
(二)广度优先搜索(BFS)
-
队列实现
queue<int> q; vector<bool> visited(n, false); q.push(root); visited[root] = true; while (!q.empty()) { int u = q.front(); q.pop(); for (int v : adj[u]) { if (!visited[v]) { visited[v] = true; q.push(v); } } }
四、最短路算法
(一)Dijkstra算法
-
适用范围
适用于非负权图,求单源最短路径。 -
算法步骤
- 初始化:所有顶点到源点的距离为无穷大,源点到自己的距离为0。
- 使用优先队列(小根堆)存储顶点,按距离从小到大排序。
- 每次取出距离最小的顶点 u,更新其邻接点 v 的距离。
-
代码实现
#include <queue> #include <vector> #include <climits> using namespace std; vector<vector<pair<int, int>>> adj; // 邻接表 vector<int> dijkstra(int start, int n) { vector<int> dist(n, INT_MAX); priority_queue<pair<int, int>, vector<pair<int, int>>, greater<>> pq; dist[start] = 0; pq.push({0, start}); while (!pq.empty()) { int u = pq.top().second; int d = pq.top().first; pq.pop(); if (d > dist[u]) continue; // 剪枝 for (auto [v, w] : adj[u]) { if (dist[u] + w < dist[v]) { dist[v] = dist[u] + w; pq.push({dist[v], v}); } } } return dist; }
(二)Floyd算法
-
适用范围
适用于所有类型的图(包括负权边,但不能有负权环),求多源最短路径。 -
算法步骤
-
初始化邻接矩阵,设 \(dist[i][j]\) 为顶点 i 到 j 的最短距离。
-
通过三重循环动态更新最短距离:
for (int k = 0; k < n; k++) { for (int i = 0; i < n; i++) { for (int j = 0; j < n; j++) { if (dist[i][k] != INT_MAX && dist[k][j] != INT_MAX) { dist[i][j] = min(dist[i][j], dist[i][k] + dist[k][j]); } } } }
-
-
代码实现
const int INF = INT_MAX; void floyd(int n) { for (int k = 0; k < n; k++) { for (int i = 0; i < n; i++) { for (int j = 0; j < n; j++) { if (dist[i][k] != INF && dist[k][j] != INF) { dist[i][j] = min(dist[i][j], dist[i][k] + dist[k][j]); } } } } }
五、树上问题
(一)DFS序
-
定义
DFS序是通过深度优先搜索遍历树时,访问每个节点的顺序。可以用于将树上的问题转化为序列问题。 -
实现
vector<int> dfsOrder; void dfs(int u, int parent) { dfsOrder.push_back(u); for (int v : adj[u]) { if (v == parent) continue; dfs(v, u); } }
(二)简单树形DP(例:没有上司的舞会)
-
问题描述
一个公司有 n 个员工,每个员工有一个快乐值。每个员工可以邀请或不邀请,但不能同时邀请一个员工和他的直接上司。目标是最大化邀请员工的总快乐值。 -
解题思路
- 使用树形DP,定义 \(dp[u][0]\) 表示不邀请节点 u 的最大快乐值,\(dp[u][1]\) 表示邀请节点 u 的最大快乐值。
- 状态转移方程:
- \(dp[u][0]=∑max(dp[v][0],dp[v][1])\)(不邀请 u,子节点可以自由选择)
- \(dp[u][1]=joy[u]+∑dp[v][0]\)(邀请 u,子节点不能邀请)
-
代码实现
vector<vector<int>> adj; vector<int> joy; vector<vector<int>> dp; void dfs(int u, int parent) { dp[u][1] = joy[u]; // 邀请当前节点 for (int v : adj[u]) { if (v == parent) continue; dfs(v, u); dp[u][0] += max(dp[v][0], dp[v][1]); // 不邀请当前节点 dp[u][1] += dp[v][0]; // 邀请当前节点,子节点不能邀请 } }



 浙公网安备 33010602011771号
浙公网安备 33010602011771号