ACM寒假集训第六次专题任务
ACM寒假集训第六次专题任务
一、最大子段和
题目:
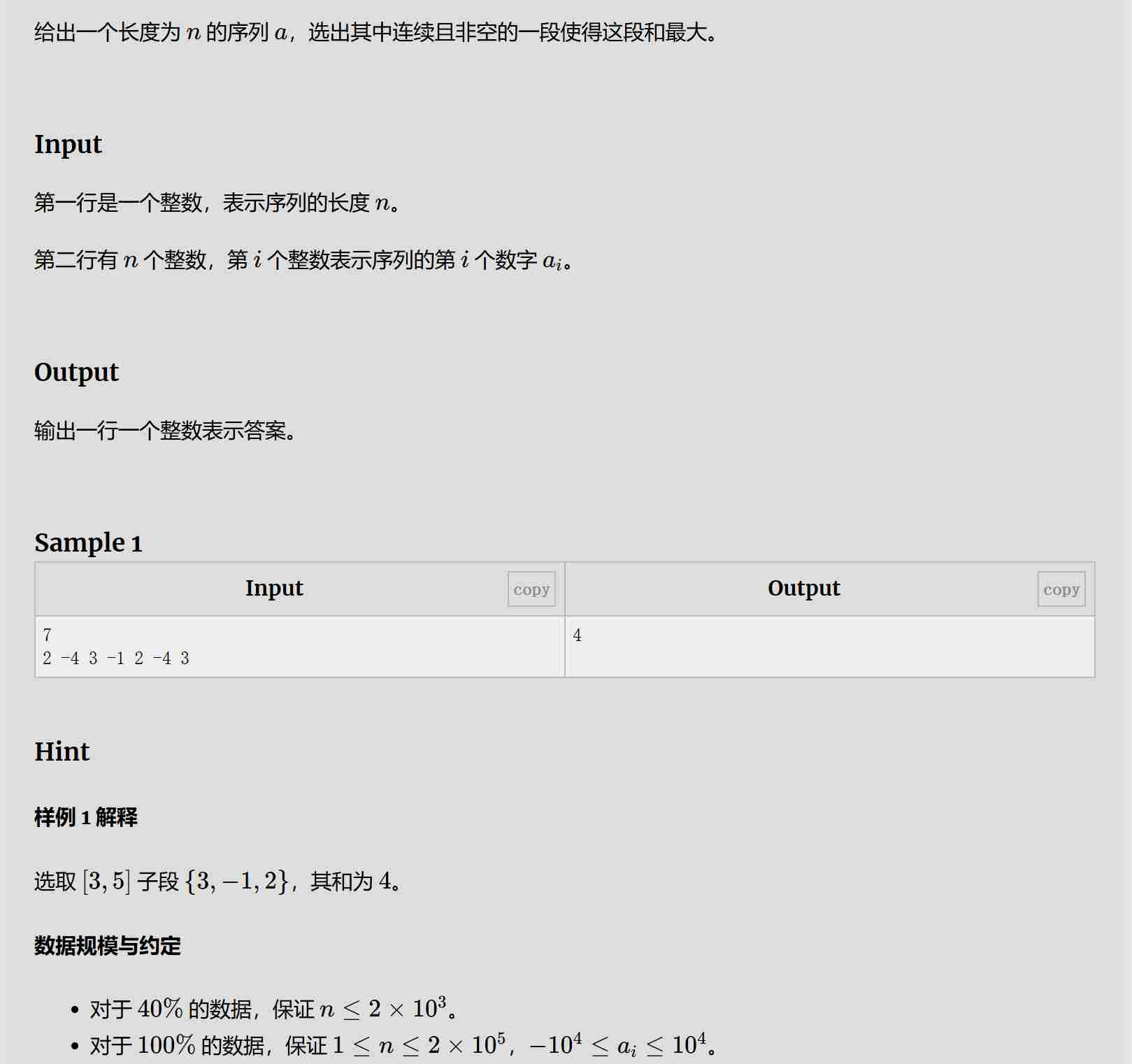
解题思路:
维护两个变量:b 表示以当前元素结尾的最大子数组和,ans 表示全局的最大子数组和。遍历数组时,对于每个元素,更新 b 为当前元素值或当前元素与前一个最大子数组和的和(取较大值),同时更新 ans 为全局最大值。最终,ans 即为所求的最大子数组和。
AC代码:
#include<iostream>
#include<algorithm>
using namespace std;
int n,a,b,ans=-2000000000;
int main()
{
cin>>n;
for(int i=1;i<=n;i++)
{
cin>>a;
if(i==1)
{
b=a;
}
else
{
b=max(a,b+a);
}
ans=max(ans,b);
}
cout<<ans;
return 0;
}
二、采药
题目:
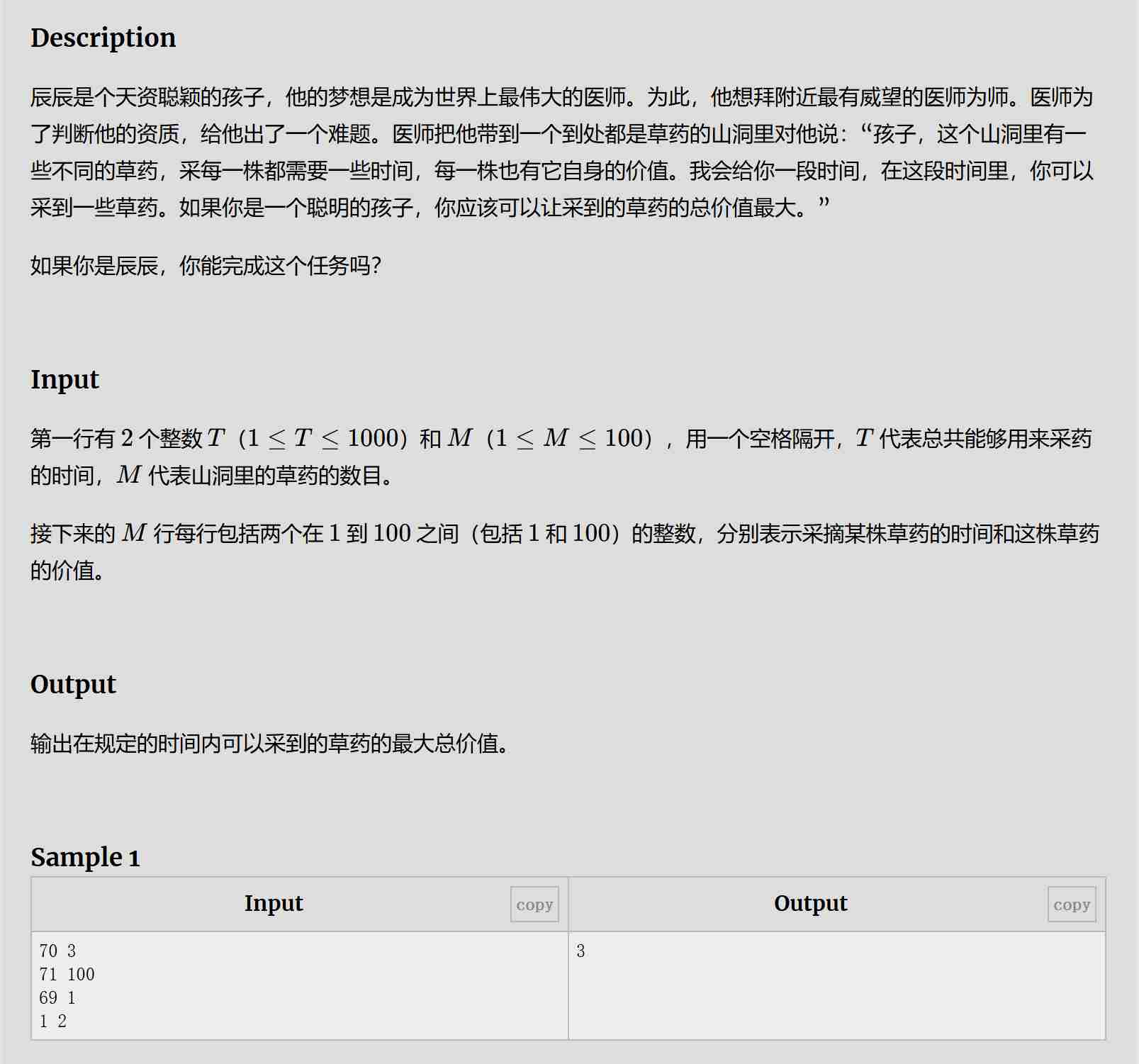

解题思路:
使用动态规划,定义f[i]为在时间i内可以采摘到的最大价值。那么,对于每种草药,我们都有两种选择:采摘或不采摘。如果采摘第i种草药,那么我们可以在j-t[i]内采摘其他草药,然后加上第i种草药的价值v[i],即f[j-t[i]]+v[i]。如果不采摘第i种草药,那么f[j]就是f[j]。因此状态转移方程为\(f[j]=max(f[j],f[j-t[i]]+v[i])\).
AC代码:
#include<iostream>
#include<algorithm>
using namespace std;
int T,M,t[1009],v[1009],f[1009];
int main()
{
cin>>T>>M;
for(int i=1;i<=M;i++)
{
cin>>t[i]>>v[i];
}
for(int i=1;i<=M;i++)
{
for(int j=T;j>=t[i];j--)
{
f[j]=max(f[j],f[j-t[i]]+v[i]);
}
}
cout<<f[T];
return 0;
}
三、宝物筛选
题目:
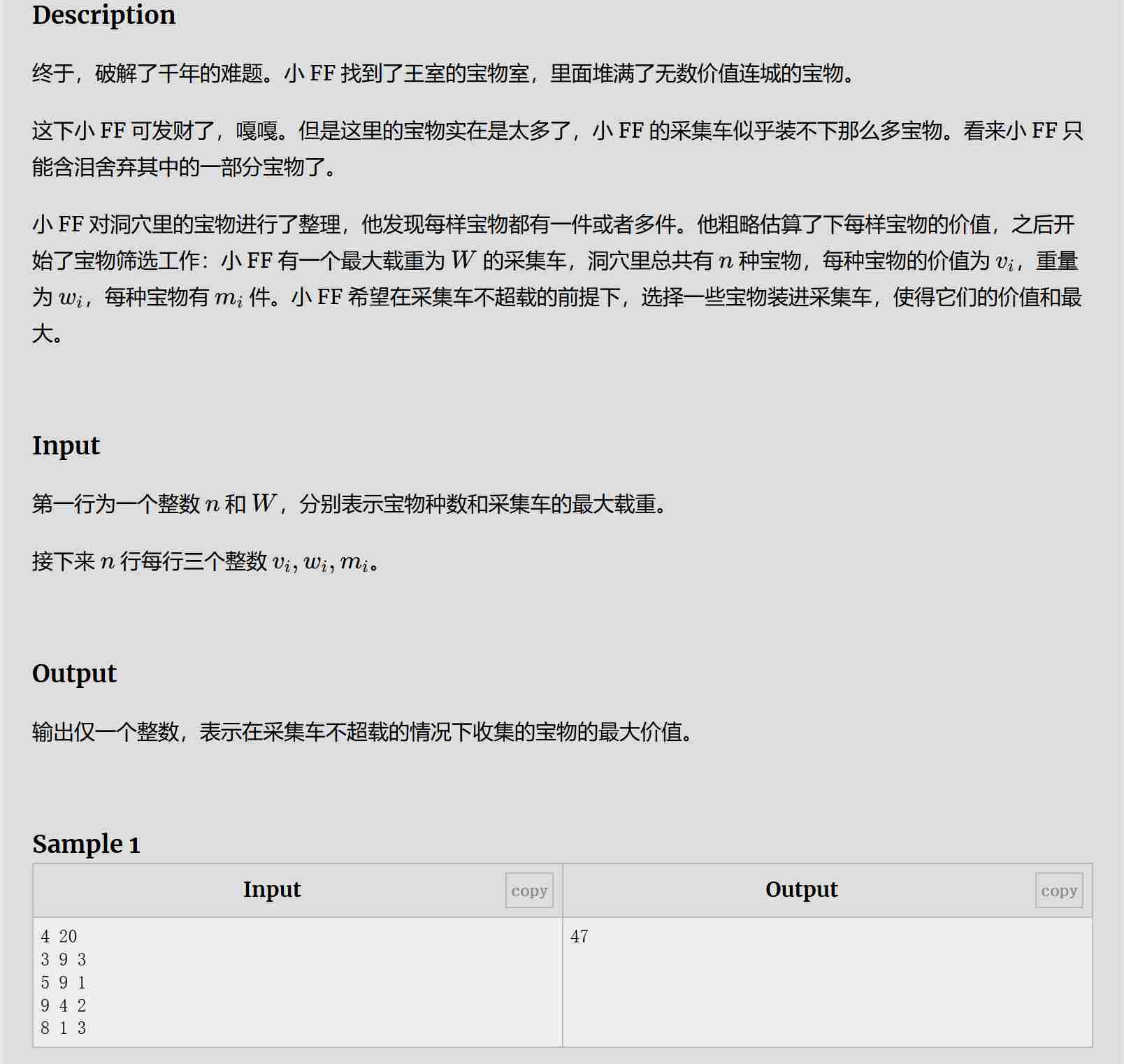
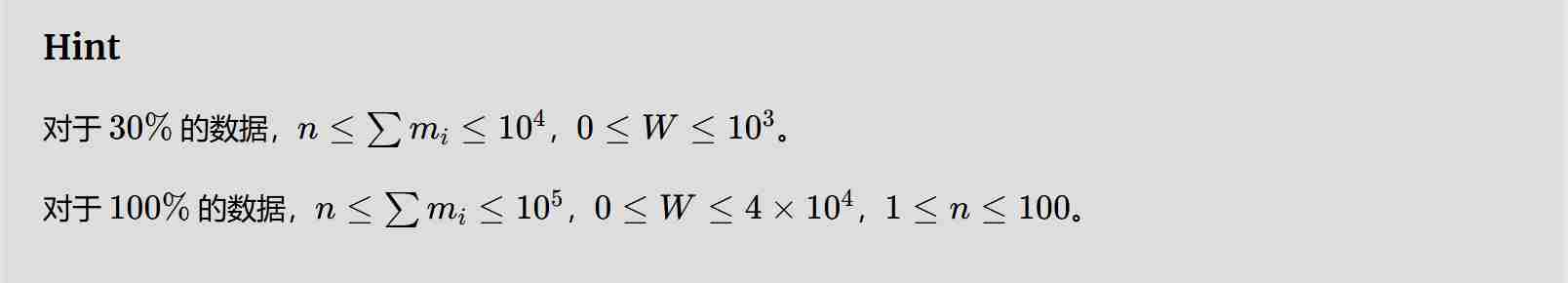
解题思路:
状态转移方程的获取参考上题,除此之外,这题的重点还有二进制拆分(优化)。
二进制拆分的核心思想是将每种宝物的数量 \(m_i\) 拆分成若干个“部分”,使得这些部分的组合可以表示出原数量范围内的所有可能值。通过这种方式,我们可以将多重背包问题转化为多个0-1背包问题,从而降低复杂度。
AC代码:
#include<iostream>
#include<algorithm>
using namespace std;
int n,W,ans,cnt=1,v[100009],w[100009],f[100009];
int main()
{
int a,b,c;
cin>>n>>W;
for(int i=1;i<=n;i++)
{
cin>>a>>b>>c;
for(int j=1;j<=c;j*=2)
{
v[++cnt]=j*a;
w[cnt]=j*b;
c-=j;
}
if(c)
{
v[++cnt]=a*c;
w[cnt]=b*c;
}
}
for(int i=1;i<=cnt;i++)
{
for(int j=W;j>=w[i];j--)
{
f[j]=max(f[j],f[j-w[i]]+v[i]);
}
}
cout<<f[W];
return 0;
}
四、最长公共子序列
题目:
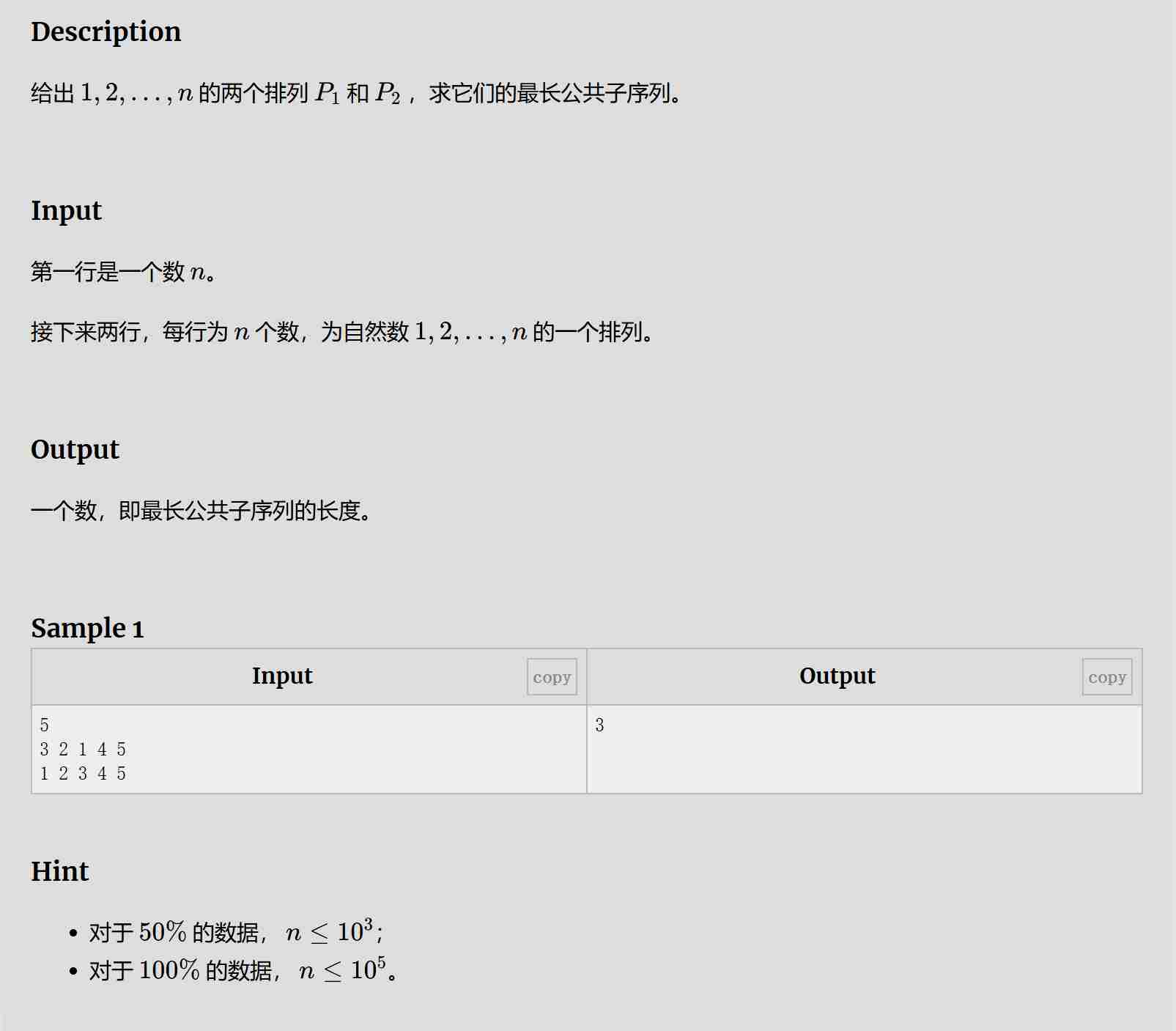
解题思路:
首先记录第一个排列中每个数字的位置,然后将第二个排列中的数字转换为它们在第一个排列中的位置,形成一个新的序列。最后,对这个新序列求最长递增子序列的长度(采用了二分查找),即为所求的最长公共子序列的长度。
AC代码:
#include<iostream>
using namespace std;
int n,a[100009],dp[100009],map[100009];
int main()
{
cin>>n;
int x;
for(int i=1;i<=n;i++)
{
cin>>x;
map[x]=i;
}
for(int i=1;i<=n;i++)
{
cin>>a[i];
a[i]=map[a[i]];
}
int len=1;
dp[1]=a[1];
for(int i=2;i<=n;i++)
{
if(dp[len]<a[i])
{
dp[++len]=a[i];
}
else
{
int l=1,r=len,mid;
while(l<=r)
{
mid=(l+r)/2;
if(dp[mid]>=a[i])
{
r=mid-1;
}
else
{
l=mid+1;
}
}
dp[l]=a[i];
}
}
cout<<len;
return 0;
}
五、Kevin and Puzzle
题目:

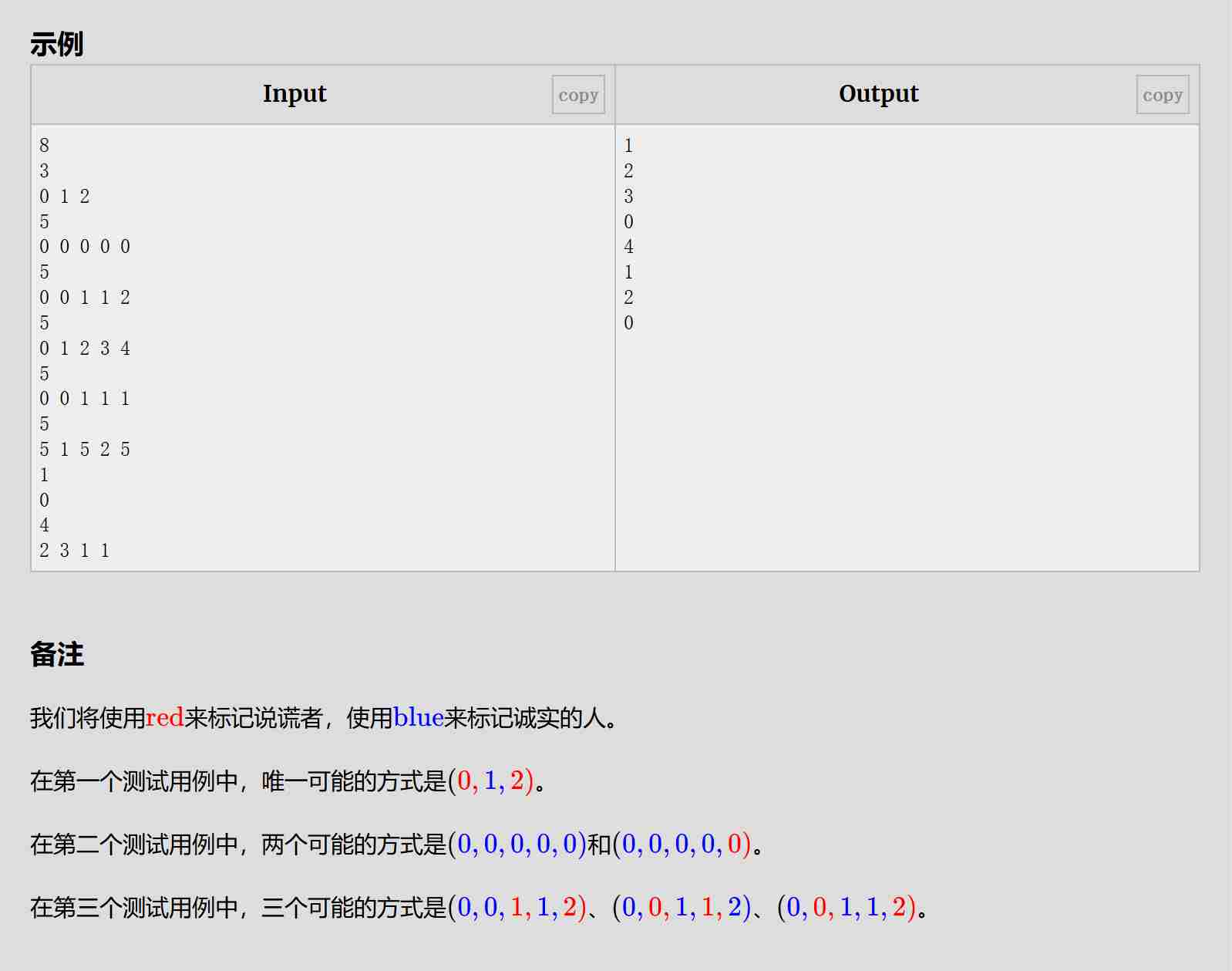
解题思路:
通过动态规划求解,定义状态 dp[i][0] 表示第 i 个同学是说谎者时的配置数量,dp[i][1] 表示第 i 个同学是诚实者时的配置数量。根据每个同学的声明(左边的说谎者数量),结合前一个同学的状态,推导出当前同学的状态。最终结果是 dp[n][0] + dp[n][1] 对 998244353 取模。
AC代码:
#include<bits/stdc++.h>
using namespace std;
const int mod=998244353,N=2e5+7;
int n,a[N],dp[N][2],t;
int main()
{
cin>>t;
while(t--){
cin>>n;
for(int i=1;i<=n;i++) cin>>a[i];
dp[1][0]=1;
if(a[1]==0)dp[1][1]=1;
else dp[1][1]=0;
for(int i=2;i<=n;i++){
dp[i][0]=dp[i-1][1];
dp[i][1]=0;
if(a[i]==a[i-1])dp[i][1]=(dp[i][1]+dp[i-1][1])%mod;
if(a[i]-1==a[i-2])dp[i][1]=(dp[i][1]+dp[i-1][0])%mod;
}
cout<<(dp[n][0]+dp[n][1])%mod<<endl;
}
return 0;
}
六、World is Mine
题目:

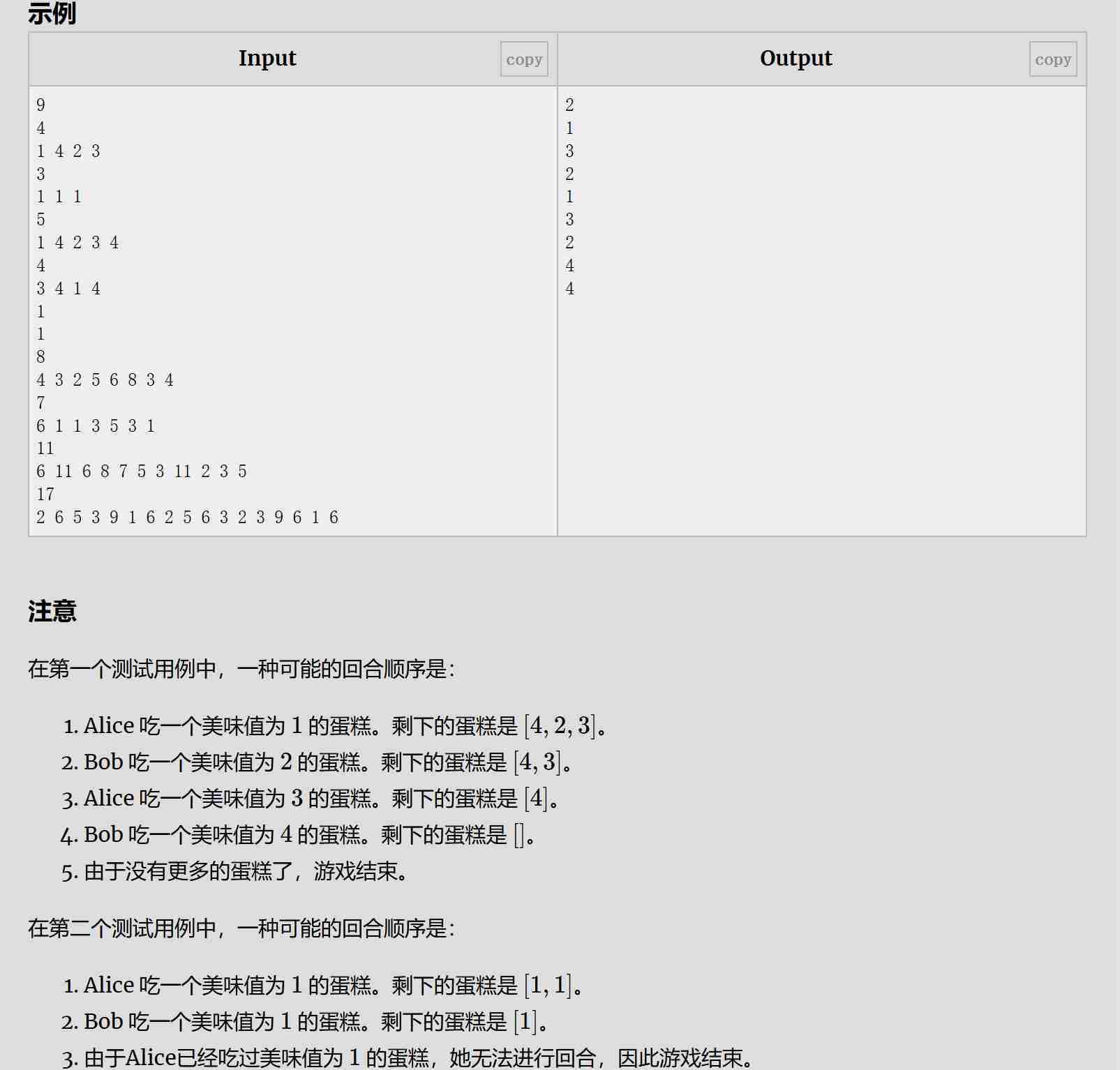
解题思路:
通过动态规划求解,定义状态 dp[i] 表示在前 i 个不同的美味值中,Bob 能够吃掉的最少蛋糕数量。通过遍历每个美味值,并更新 dp 数组,最终结果是 N - i,其中 i 是最大的满足 dp[i] != INF 的索引。这样可以确保 Alice 吃掉的蛋糕数量最大化。
AC代码:
#include <iostream>
using namespace std;
const int MAXN = 200005;
const int INF = 1000000000;
void solve() {
int n;
cin >> n;
int cnt[MAXN] = {0};
for (int i = 1; i <= n; i++) {
int a;
cin >> a;
cnt[a]++;
}
int useful[MAXN], usefulSize = 0;
for (int i = 1; i <= n; i++) {
if (cnt[i] > 0) {
useful[usefulSize++] = cnt[i];
}
}
int N = usefulSize;
int dp[MAXN];
for (int i = 0; i <= N; i++) {
dp[i] = INF;
}
dp[0] = 0;
for (int i = 1; i <= N; i++) {
for (int j = i - 1; j >= 0; j--) {
if (dp[j] + useful[i - 1] <= i - j - 1) {
if (dp[j] + useful[i - 1] < dp[j + 1]) {
dp[j + 1] = dp[j] + useful[i - 1];
}
}
}
}
for (int i = N; i >= 0; i--) {
if (dp[i] != INF) {
cout << N - i << "\n";
return;
}
}
}
int main() {
int T;
cin >> T;
while (T--) {
solve();
}
return 0;
}
学习总结
动态规划(Dynamic Programming,简称DP)是一种通过将复杂问题分解为更简单的子问题来求解的算法思想。它在解决具有重叠子问题和最优子结构特性的问题时非常有效。以下是动态规划学习的总结,包括其核心概念、常见类型、解题步骤和一些经典应用。
动态规划的核心概念
1. 重叠子问题
动态规划适用于那些可以通过重复计算相同子问题来解决的问题。例如,在计算斐波那契数列时,F(n) = F(n-1) + F(n-2),其中 F(n-1) 和 F(n-2) 是重复出现的子问题。
2. 最优子结构
如果一个问题的最优解可以由其子问题的最优解组合而成,那么这个问题具有最优子结构。例如,在最长递增子序列(LIS)问题中,长度为 k 的LIS可以通过长度为 k-1 的LIS加上一个合适的元素得到。
3. 状态与状态转移
动态规划的核心是定义状态和状态转移方程:
- 状态:表示问题的中间结果,通常是一个数组或表格。
- 状态转移方程:描述如何从已知状态推导出新的状态。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号