ACM寒假集训第二次专题任务
ACM寒假集训第二次专题任务
一、二分查找
题目:
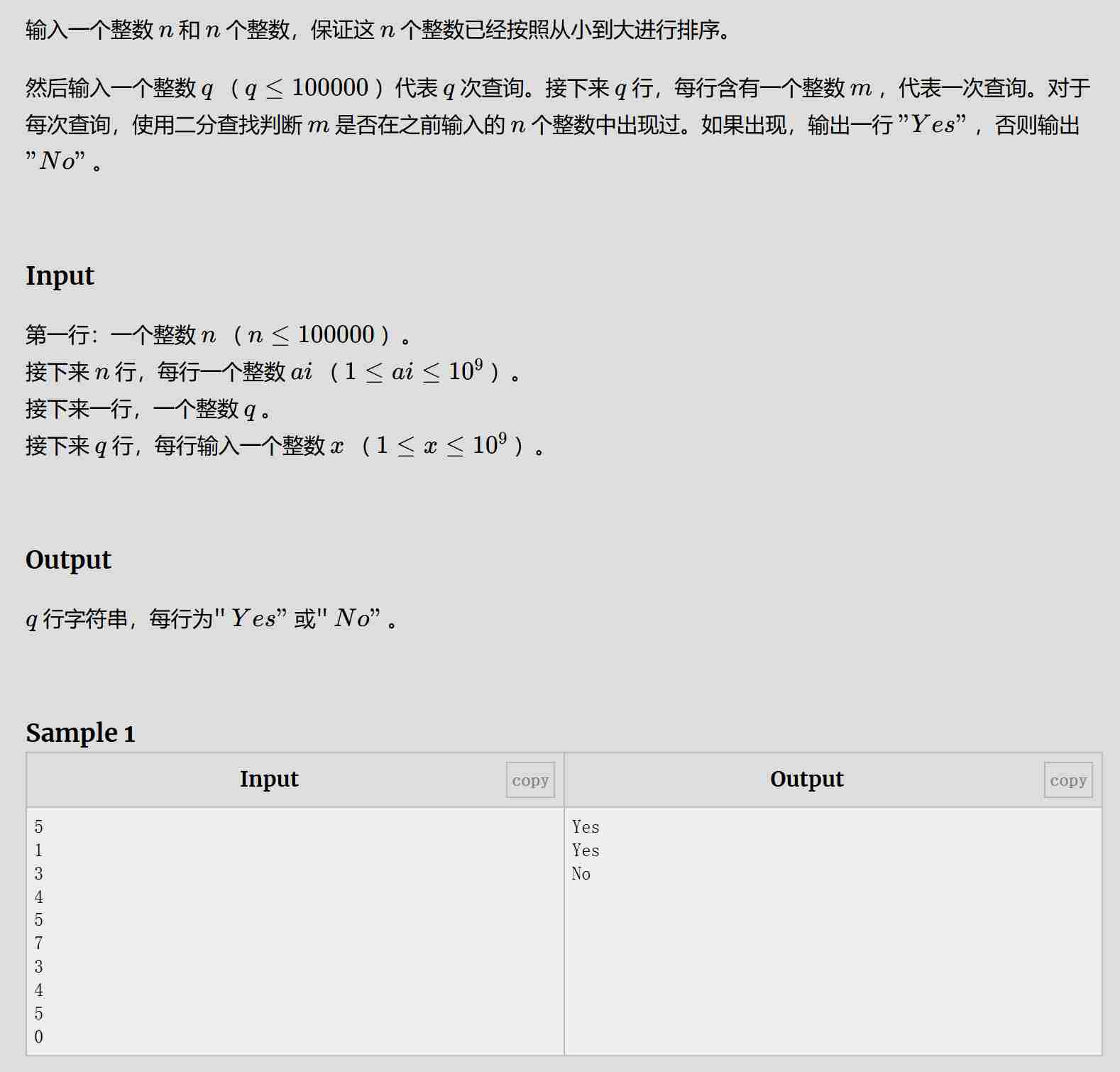
解题思路:
输入数据后把每一个x单独拎出来,通过二分查找检验是否存在于被测数组中。
AC代码:
#include<iostream>
using namespace std;
int main()
{
int n,a[100000]={0},q,x[100000];
cin>>n;
for(int i=0;i<n;i++)
{
cin>>a[i];
}
cin>>q;
for(int i=0;i<q;i++)
{
cin>>x[i];
}
for(int i=0;i<q;i++)
{
int l=0,r=n-1,f=0;
while(l<=r)
{
int mid=(l+r)/2;
if(a[mid]==x[i])
{
cout<<"Yes"<<endl;
f=1;
break;
}
else if(a[mid]<x[i])
{
l=mid+1;
}
else if(a[mid]>x[i])
{
r=mid-1;
}
}
if(f==0)
{
cout<<"No"<<endl;
}
}
return 0;
}
二、A-B 数对
题目:
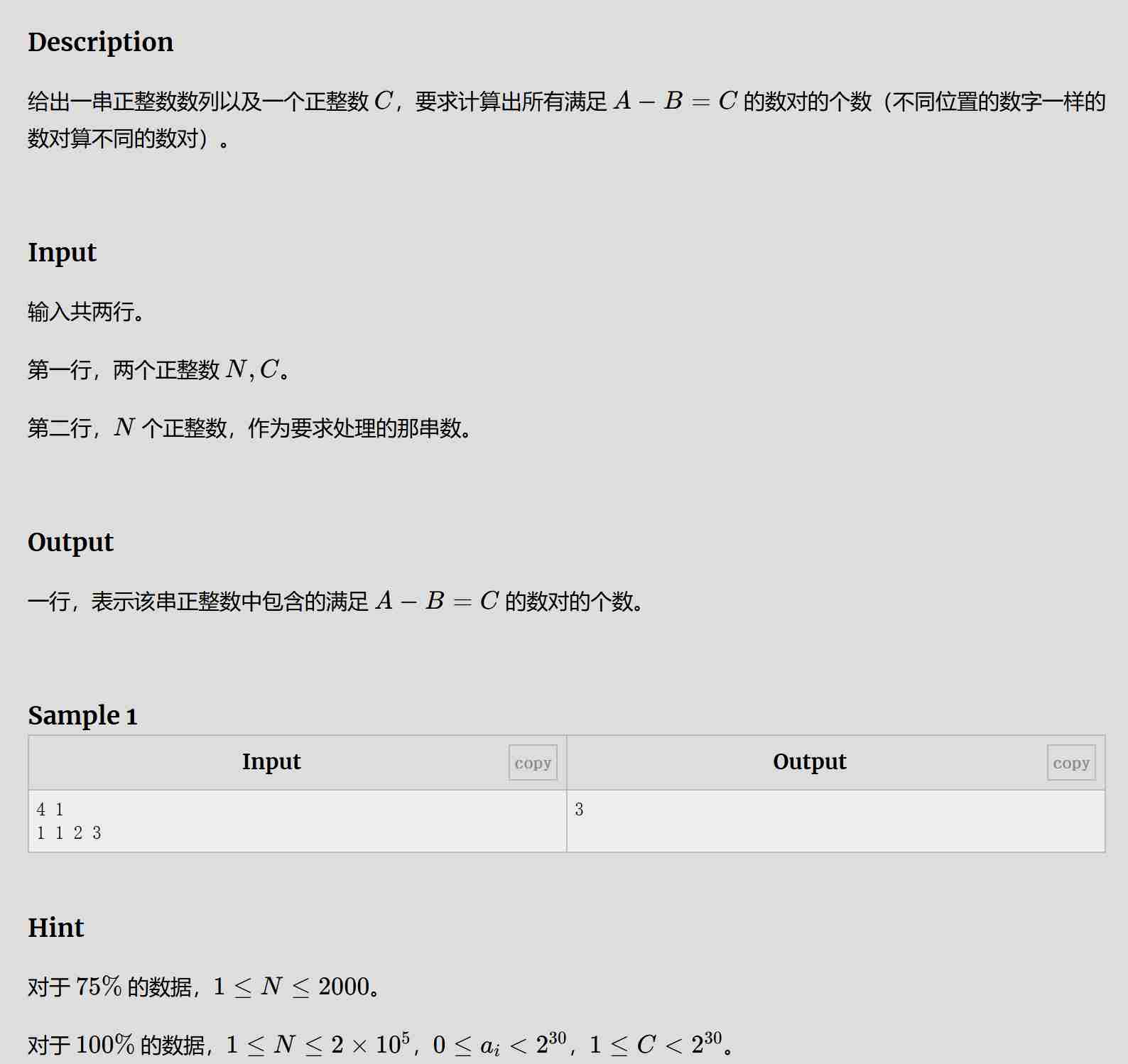
解题思路:
-
分析题目:一个数对包含A,B,C三个数字,其中C为输入数据(可看作已知),同时分析A与B比较困难,对A-B=C进行改写,得A=C+B;
-
因为A、B都存在于输入的数组中,所以B也可以看作已知。此时只需要分析输入数组中A是否存在。
-
对输入数组从小到大进行排序,再通过二分查找进行搜索。
注:需要注意数值取值范围。
AC代码:
#include<iostream>
#include<algorithm>
using namespace std;
int lower(int l,int r,int target,int* num)
{
int ans=0;
while(l<=r)
{
int mid=(l+r)/2;
if(num[mid]==target)
{
ans=mid;
r=mid-1;
}
else if(num[mid]<target)
{
l=mid+1;
}
else if(num[mid]>target)
{
r=mid-1;
}
}
return ans;
}
int upper(int l,int r,int target,int* num)
{
int ans=0;
while(l<=r)
{
int mid=(l+r)/2;
if(num[mid]==target)
{
ans=mid;
l=mid+1;
}
else if(num[mid]<target)
{
l=mid+1;
}
else if(num[mid]>target)
{
r=mid-1;
}
}
return ans;
}
int main()
{
int N,C,num[200000]={0};
cin>>N>>C;
for(int i=0;i<N;i++)
{
cin>>num[i];
}
sort(num,num+N);
long long sum=0;
for(int i=0;i<N;i++)
{
int A=num[i]+C;
int ans=0;
int l=lower(0,N,A,num);
int r=upper(0,N,A,num);
if(l==r)
{
if(l==0)
{
ans=0;
}
else
ans=1;
}
else
ans=r-l+1;
sum+=ans;
}
cout<<sum<<endl;
return 0;
}
三、分巧克力
题目:

解题思路:
-
分析题目:求最大边长,可通过二分查找确定所求边长。
-
先明确左右端点,边长最小为1,故l=1;边长最大为100000,故r=100000。
-
再明确如何检验mid是否合理:(矩形的长/mid)*(矩形的宽/mid)即为该矩形所能切割的最大个数,与K比较,比K大说明mid还可以增大,比K小说明mid应该减小。
AC代码:
#include<iostream>
using namespace std;
struct square{
int H;
int W;
};
bool check(int mid,int N,int K,square a[])
{
int cut=0;
for(int i=0;i<N;i++)
{
cut+=(a[i].H/mid)*(a[i].W/mid);
}
if(cut>=K)
{
return 1;
}
else
{
return 0;
}
}
int main()
{
int N,K;
cin>>N>>K;
square a[100000];
for(int i=0;i<N;i++)
{
cin>>a[i].H>>a[i].W;
}
int l=1,r=1e5,ans=1;
while(l<=r)
{
int mid=(r+l)/2;
if(check(mid,N,K,a))
{
l=mid+1;
ans=mid;
}
else
{
r=mid-1;
}
}
cout<<ans;
return 0;
}
四、卡牌
题目:
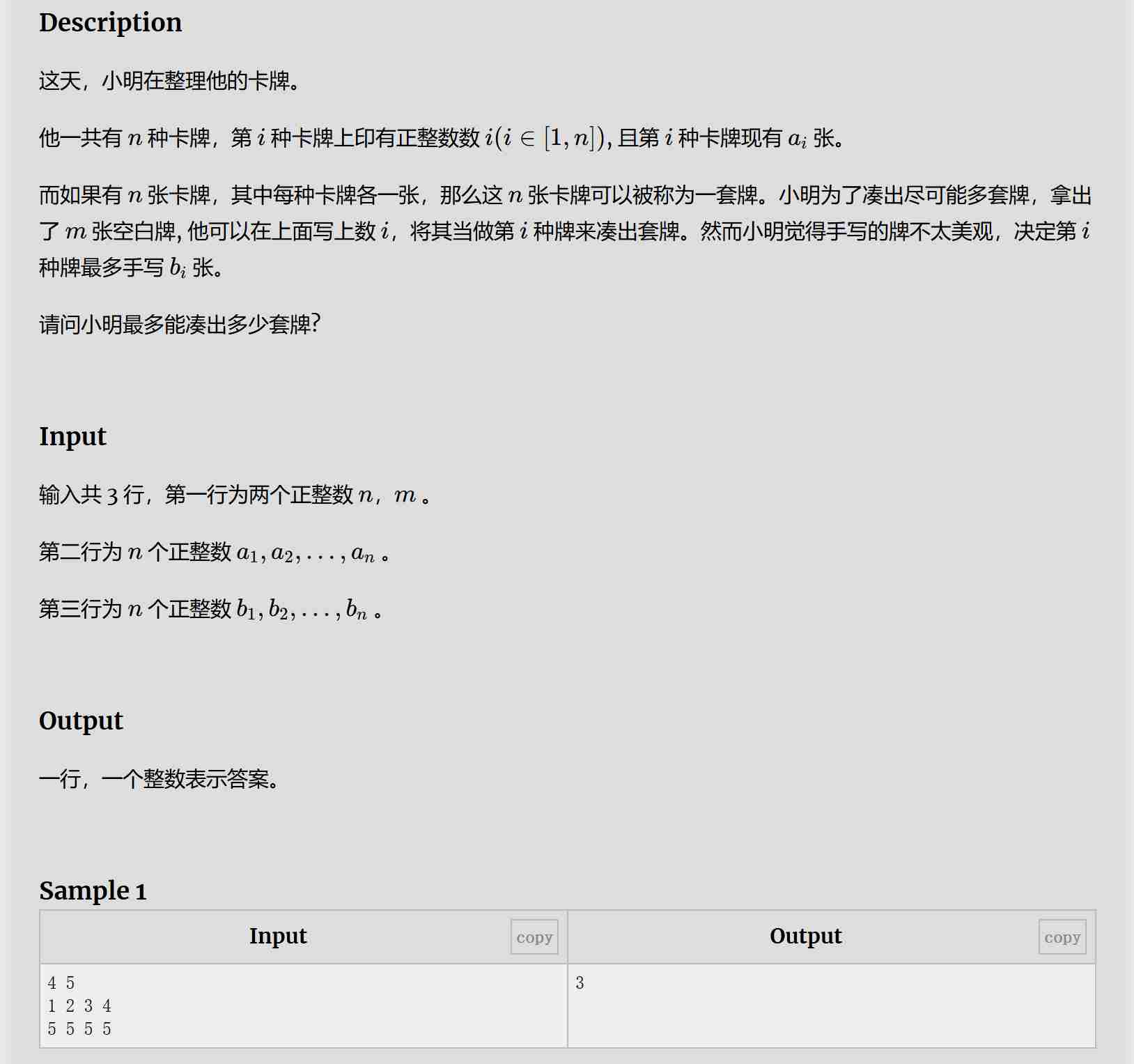

解题思路:
本题使用二分答案。
-
明确查找对象:凑出的牌的套数;
-
确定check逻辑:限制可分成两个,一个是凑出mid套牌所需补充的牌数不得超过m;另一个是mid套牌不能大于某一牌现有牌数和对应限制补充牌数的最大值(
max(a[i]+b[i])); -
通过对两个check的分析对端点进行左右移动。
AC代码:
#include<iostream>
#include<vector>
using namespace std;
struct card{
long long a;
long long b;
};
long long smaller(long long a,long long b)
{
if(a<b)
return a;
else
return b;
}
long long max(long long big[],long long n)
{
int ma=big[0];
for(int i=0;i<n;i++)
{
if(big[i]>ma)
ma=big[i];
}
return ma;
}
bool check(long long mid,long long n,long long m,vector<card>& c)
{
long long need=0;
for(long long i=0;i<n;i++)
{
long long add=smaller(mid-c[i].a,c[i].b);
if(add<=0)
{
continue;
}
else
{
need+=add;
}
}
return need<=m;
}
bool check2(long long mid,long long n,long long big[])
{
for(long long i=0;i<n;i++)
{
if(mid>big[i])
{
return 0;
}
}
return 1;
}
int main()
{
long long n,m;
cin>>n>>m;
long long big[n];
vector<card> c(n);
for(long long i=0;i<n;i++)
{
cin>>c[i].a;
}
for(long long i=0;i<n;i++)
{
cin>>c[i].b;
big[i]=c[i].a+c[i].b;
}
long long l=0,r=max(big,n),ans=0;
while(l<=r)
{
long long mid=(r+l)/2;
if(check(mid,n,m,c)&&check2(mid,n,big))
{
l=mid+1;
ans=mid;
}
else
{
r=mid-1;
}
}
cout<<ans;
return 0;
}
五、书的复制
题目:

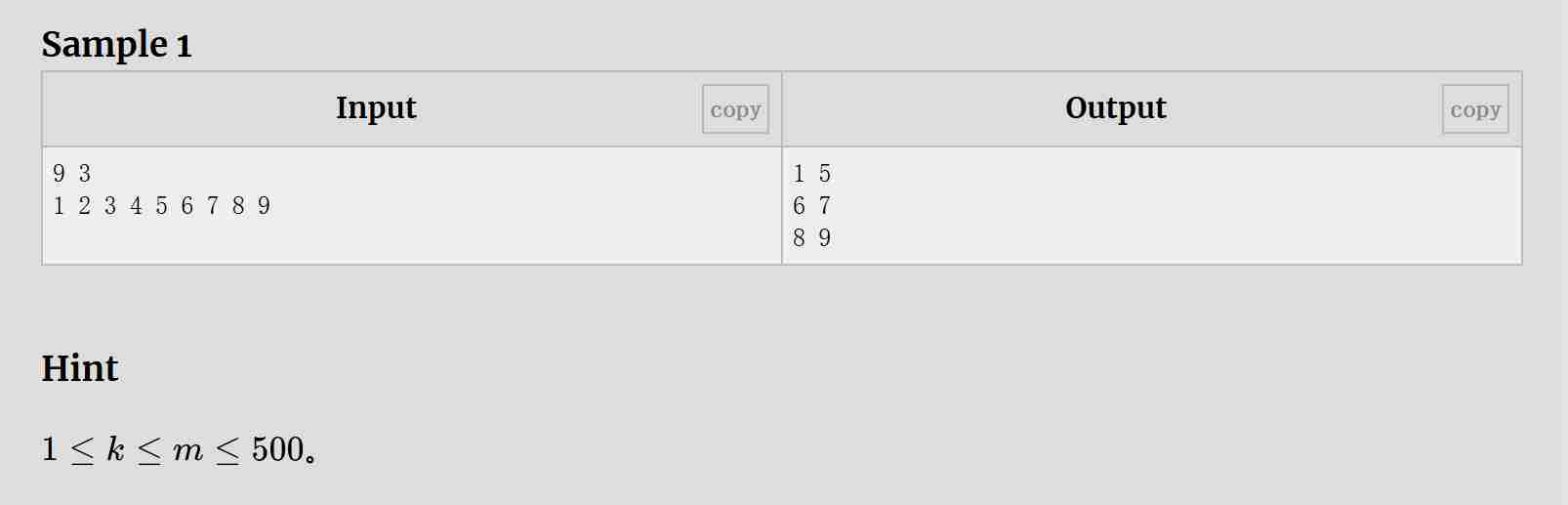
解题思路:
- 输入处理:读取书的数量
m、人的数量k以及每本书的页数。 - 二分查找最短复制时间:确定二分查找的左右边界,不断调整中间值,通过检查函数判断该时间是否满足要求,逐步缩小查找范围,直到找到最短复制时间。
- 书籍分配:根据最短复制时间,从后往前分配书籍,使得前面的人抄写的书尽可能少。
- 输出结果:输出每个人抄写的书的起始编号和终止编号。
AC代码:
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int K = 500;
int m, k, a[K + 5];
int st[K + 5], ed[K + 5];
inline int read() {
int x = 0;
bool f = 1;
char ch = getchar();
for (; ch < '0' || ch > '9'; ch = getchar()) f ^= (ch == '-');
for (; ch >= '0' && ch <= '9'; ch = getchar()) x = (x << 1) + (x << 3) + (ch ^ 48);
return f ? x : -x;
}
bool check(int limit) {
int people = 1;
int remainingPages = limit;
for (int i = 1; i <= m; ++i) {
if (a[i] > remainingPages) {
people++;
remainingPages = limit;
}
remainingPages -= a[i];
}
return people <= k;
}
void solve() {
m = read(), k = read();
int left = 0, right = 0;
for (int i = 1; i <= m; ++i) {
a[i] = read();
left = max(left, a[i]);
right += a[i];
}
while (left < right) {
int mid = left + (right - left) / 2;
if (check(mid)) {
right = mid;
} else {
left = mid + 1;
}
}
ed[k] = m, st[1] = 1;
int currentLimit = left;
for (int i = k, j = m; i; --i) {
while (currentLimit >= a[j] && j) {
currentLimit -= a[j];
j--;
}
st[i] = j + 1;
ed[i - 1] = j;
currentLimit = left;
}
for (int i = 1; i <= k; ++i) {
cout << st[i] << ' ' << ed[i] << '\n';
}
}
signed main() {
solve();
return 0;
}
六、青蛙过河
题目:
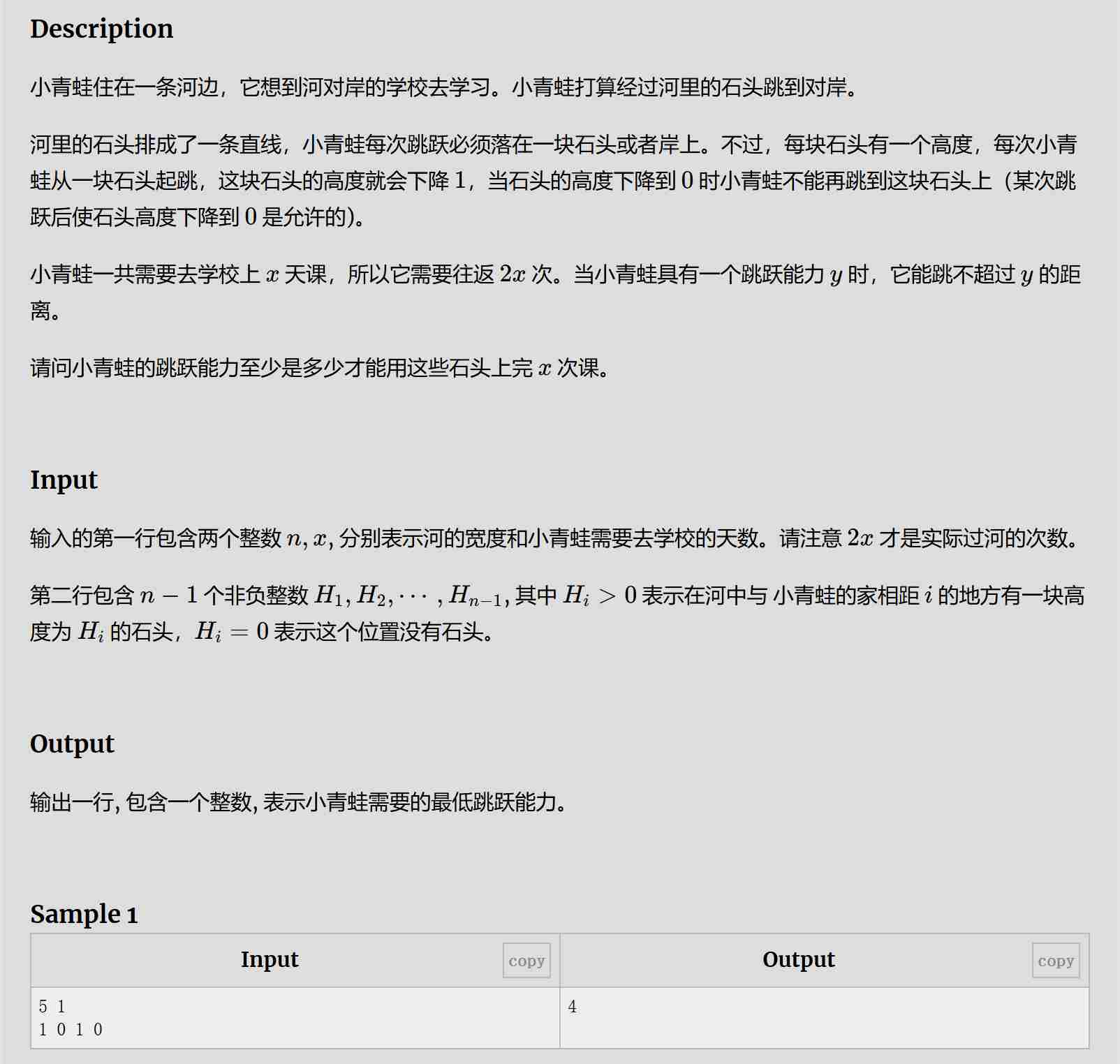

解题思路:
- 输入处理:读取数组的长度
n、目标值x以及数组元素H,同时对输入的n进行有效性检查。 - 构建前缀和数组:通过遍历数组
H,计算并存储前缀和到数组sum中,以便后续快速计算任意子数组的和。 - 二分查找最小长度:在可能的长度范围
[1, n]内进行二分查找,对于每个中间长度mid,使用check函数检查是否所有长度为mid的子数组的和都满足条件。 - 输出结果:二分查找结束后,输出满足条件的最小长度。
AC代码:
#include <iostream>
#include <cstdio>
using namespace std;
const int N = 1e5;
int n, x, H[N + 5], sum[N + 5];
inline int read() {
int x = 0;
bool f = 1;
char ch = getchar();
for (; ch < '0' || ch > '9'; ch = getchar())
f ^= (ch == '-');
for (; ch >= '0' && ch <= '9'; ch = getchar())
x = (x << 1) + (x << 3) + (ch ^ 48);
return f? x : -x;
}
bool check(int mid) {
for (int i = 1; i + mid - 1 < n; ++i) {
int L = i, R = i + mid - 1;
if (sum[R] - sum[L - 1] < 2 * x) return 0;
}
return 1;
}
void Kafka() {
n = read();
if (n < 1 || n > N) {
cerr << "Invalid value of n" << endl;
return;
}
x = read();
for (int i = 1; i < n; ++i) {
H[i] = read();
}
for (int i = 1; i < n; ++i) sum[i] = H[i] + sum[i - 1];
int L = 1, R = n;
while (L < R) {
int mid = L + (R - L) / 2;
if (check(mid)) {
R = mid;
} else {
L = mid + 1;
}
}
cout << L << '\n';
}
int main() {
Kafka();
return 0;
}
学习总结
二分查找
二分查找适用于有序数据、具有单调性的查找目标以及数据规模较大的场景,能够显著提高查找效率。
思路简单,上手快,可套模板。但需搞清端点取值及加不加等号的问题。
二分答案
以二分查找为基础,明确需要查找的答案(例如,以上题目中正方形边长)是什么,并且设计如何检验mid合理性(难点所在)。
还是得多做。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号