最优贸易

题目地址

题意

  给定一个图，找到一条从1~n的路径，使得路径上能选出两个点p，q（先经过p在经过q）并且节点q的节点减去节点p的权值最大。

做法

  1.先以1为起点，跑一遍spfa，求出数组\(D[x]\)表示从节点 1 到节点 x 的所有路径中，能过经过的权值最小的节点的权值，\(D[x]\) 与求最短路类似，只需把最短路中用 \(D[x] + w[w,y]\)更新 \(D[y]\) 改成 \(D[y] = min(D[x],price[y])\) 其中\(price[i]\) 表示第i个节点的权值，\(w[x,y]\) 表示最短路中，从x走到y的权值（此处不会用到)。
  2.在以n为起点，在反向图中，跑一遍spfa，求出数组\(F[x]\)这里表示从节点 n 到节点 x 的所有路径中，能经过的权值最大的节点的权值，\(F[y] = max(F[x],price[y]\)。
  3.最后枚举每个节点x，用\(F[x] - D[x]\)更新答案。

参考代码

#include <iostream>
#include <algorithm>
#include <cstdio>
#include <cstring>
#include <queue>
using namespace std;

const int N = 100010, M = 500010 * 4;

int h[N],rh[N],e[M],ne[M],idx;
int d1[N],d2[N];
int w[N];
int n,m;
bool st[N];
void add(int h[],int a,int b)
{
    e[idx] = b,ne[idx] = h[a],h[a] = idx ++;
}
// flag： true表示正向图， false表示反向图
void spfa(int h[],int dist[],int start,bool flag)
{
    memset(st,false,sizeof st);
    queue<int> q;
    dist[start] = w[start];
    q.push(start);
    while(q.size())
    {
        int t = q.front();q.pop();
        st[t] = false;
        for(int i = h[t]; ~ i; i = ne[i])
        {
            int j = e[i];
            if((flag && dist[j] > min(dist[t],w[j])) || (! flag && dist[j] < max(dist[t],w[j])))  // 满足其中一个就行
            {
                if(flag) dist[j] = min(dist[t],w[j]); // 根据flag的值来赋值。
                else dist[j] = max(dist[t],w[j]);
                if(! st[j])
                {
                    st[j] = true;
                    q.push(j);
                }
            }
        }
    }

}

int main()
{
    scanf("%d%d",&n,&m);
    memset(h,-1,sizeof h);
    memset(rh,-1,sizeof rh);
    for(int i = 1; i <= n; i ++) scanf("%d",&w[i]);

    for(int i = 1; i <= m; i ++)
    {
        int a,b,c;
        scanf("%d%d%d",&a,&b,&c);
        add(h,a,b);
        add(rh,b,a); // 建立反向边
        if(c == 2) add(h,b,a),add(rh,a,b);
    }
    memset(d1,0x3f,sizeof d1); // 求最小值，数组初始化无穷大
    spfa(h,d1,1,true);         // 第一步求出 D[x],这里使用d1
    spfa(rh,d2,n,false);       // 第二步求出 F[x],这里使用d2
    int res = 0;
    // 对应上面第三步
    for(int i = 1; i <= n; i ++){
        //cout << d1[i] << " " << d2[i] << endl;
        res = max(res,d2[i] - d1[i]);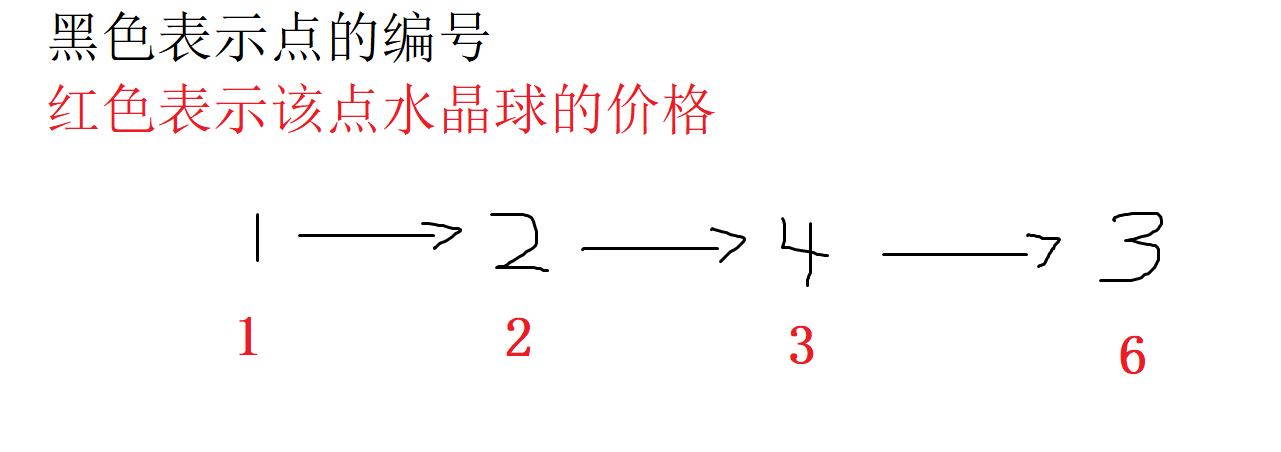![](https://img2020.cnblogs.com/blog/1925085/202010/1925085-20201027210248300-164646963.png)


    }
    cout << res <<endl;
}

特别说明

  本题不能使用dijkstra，因为dijkstra本身就是基于贪心，第一次选取的点即为最小点，如果不是最小点，就会出错，比如有两个点：1和2，价格分别是2和1，一共有两条边：1->2，和2->1，那么最初优先队列中只有一个点1,此时1被弹出，它的最小价格是2，但2并不是最终的最小值。所以dijkstra算法是不适用的。

为什么求最大值不能在原图跑???

  因为并不是所有点都可以到达终点，必须保证，从1走到x号点的同时还要保证x能走到n号点，例如下面：

如果正向求一边，发现最大值是 F[3] - D[3] = 6 - 1 = 5 ,但是这不满足要求，因为3最后不能走到4，正确的答案应该是 F[4] - D[4] = 3 - 1 = 2
所以我们需要从反向图求最大值，即4压根都走不到3，F[3] = 0，D[3] = 6,我们在求答案的时候 res = max(res,F[3] - D[3]) 是不会更新res的，因为res初始为0。