dp 未分类题目

2484. Count Palindromic Subsequences

Given a string of digits s, return the number of palindromic subsequences of s having length 5. Since the answer may be very large, return it modulo 109 + 7.

Note:

• A string is palindromic if it reads the same forward and backward.
• A subsequence is a string that can be derived from another string by deleting some or no characters without changing the order of the remaining characters.

Example 1:

Input: s = "103301"
Output: 2
Explanation: 
There are 6 possible subsequences of length 5: "10330","10331","10301","10301","13301","03301". 
Two of them (both equal to "10301") are palindromic.

Example 2:

Input: s = "0000000"
Output: 21
Explanation: All 21 subsequences are "00000", which is palindromic.

Example 3:

Input: s = "9999900000"
Output: 2
Explanation: The only two palindromic subsequences are "99999" and "00000". 

Constraints:

• 1 <= s.length <= 104
• s consists of digits.

  

   

 

class Solution {
    public int countPalindromes(String s) {
        // 计算左侧的两位排列个数
        int[][][] l2r = countLeftToRight(s);
        // 计算右侧的两位排列个数
        int[][][] r2l = countRightToLeft(s);
        int MOD = 1000_000_007;
        long result = 0;
        // 从第3个元素开始，计算左右侧100中情况的count，相加
        for(int i = 2; i < s.length() - 2; i++) {
            for(int j = 0; j < 10; j++) {
                for(int k = 0; k < 10; k++) {
                    result += 1l * l2r[i - 1][j][k] * r2l[i + 1][j][k];
                    result = result % MOD;
                }
            }
        }
        return (int)result;
    }

    private int[][][] countLeftToRight (String s) {
        // 记录当前某数字出现的次数
        int[] cnt = new int[10];
        int[][][] count = new int[s.length()][10][10];
        // i为当前第二个数字的位置
        for(int i = 0; i < s.length(); i++) {
            int c = s.charAt(i) - '0';
            if(i > 0) {
                // j 为第一个数字 0～9
                for(int j = 0; j < 10; j++) {
                    // k 为第二个数字 0～9
                    for(int k = 0; k < 10; k++) {
                        count[i][j][k] = count[i - 1][j][k];
                        // 如果k是当前数字，那么当前的count要加上
                        if(c == k) count[i][j][k] += cnt[j];
                    }
                }
            }
            cnt[c]++;
        }
        return count;
    }

    private int[][][] countRightToLeft (String s) {
        // 记录当前某数字出现的次数
        int[] cnt = new int[10];
        int[][][] count = new int[s.length()][10][10];
        for(int i = s.length() - 1; i >= 0; i--) {
            int c = s.charAt(i) - '0';
            if(i < s.length() - 1) {
                for(int j = 0; j < 10; j++) {
                    for(int k = 0; k < 10; k++) {
                        count[i][j][k] = count[i + 1][j][k];
                        if(c == k) count[i][j][k] += cnt[j];
                    }
                }
            }
            cnt[c]++;
        }
        return count;
    }
}

3122. Minimum Number of Operations to Satisfy Conditions

You are given a 2D matrix grid of size m x n. In one operation, you can change the value of any cell to any non-negative number. You need to perform some operations such that each cell grid[i][j] is:

• Equal to the cell below it, i.e. grid[i][j] == grid[i + 1][j] (if it exists).
• Different from the cell to its right, i.e. grid[i][j] != grid[i][j + 1] (if it exists).

Return the minimum number of operations needed.

Example 1:

Input: grid = [[1,0,2],[1,0,2]]

Output: 0

Explanation:

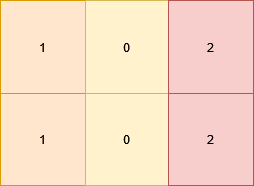
All the cells in the matrix already satisfy the properties.

Example 2:

Input: grid = [[1,1,1],[0,0,0]]

Output: 3

Explanation:

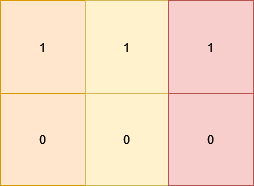
The matrix becomes [[1,0,1],[1,0,1]] which satisfies the properties, by doing these 3 operations:

• Change grid[1][0] to 1.
• Change grid[0][1] to 0.
• Change grid[1][2] to 1.

Example 3:

Input: grid = [[1],[2],[3]]

Output: 2

Explanation:

There is a single column. We can change the value to 1 in each cell using 2 operations.

Constraints:

• 1 <= n, m <= 1000
• 0 <= grid[i][j] <= 9

class Solution {
    /**
    思路：题目实际要求同一列数据要一样，相邻列的数据不能一样
    每一列数据都有10种选择：0~9, 这列的下一列数据也有0~9 10种选择
    给定下一列数据的0~9 10种选择的cost情况下， 
    只需要判断当前列N = 0~9 10种情况： 
         当前列选N的cost = 自身列全部置为N的cost + 下一列数据的不选择N的最小cost

    边界条件：最后一列数据的"下一列cost" 为 0
     */
    public int minimumOperations(int[][] grid) {
        int[] result = helper(grid, 0);
        int min = Integer.MAX_VALUE;
        for(int cost : result) {
            min = Math.min(min, cost);
        }
        return min;
    }
    private int[] helper(int[][] grid, int col) {
        int m = grid.length, n = grid[0].length;
        int[] result = new int[10];
        // 边界条件：最后一列数据的"下一列cost" 为 0
        if(col == n) return new int[10];

        // 初始化当前列10种方案的cost为无穷大
        Arrays.fill(result, Integer.MAX_VALUE);
        // 统计当前列频次分布
        int[] count = cnt(grid, col);
        // 计算下一列的10种情况cost
        int[] next = helper(grid, col + 1);
        // 计算当前列选去N:0~9 10种情况下的cost，
        for(int N = 0; N < 10; N++) {
            int selfCost = m - count[N];
            // 当前列选的cost = 自身列全部置为N的cost + 下一列数据的不选择N的最小cost
            result[N] = selfCost + min(next, N);
        }
        return result;
    }
    //统计某列的各数字个数
    private int[] cnt(int[][] grid, int col) {
        int[] result = new int[10];
        for(int i = 0; i < grid.length; i++) {
            result[grid[i][col]]++;
        }
        return result;
    }
    //给定0～9统计数据 和 val，找出val除外
    private int min(int[] last, int val) {
        int min = Integer.MAX_VALUE;
        for(int i = 0; i < 10; i++) {
            if(i != val) min = Math.min(min, last[i]);
        }
        return min;
    }
}