parenthesis 相关题目

2116. Check if a Parentheses String Can Be Valid

Medium

A parentheses string is a non-empty string consisting only of '(' and ')'. It is valid if any of the following conditions is true:

• It is ().
• It can be written as AB (A concatenated with B), where A and B are valid parentheses strings.
• It can be written as (A), where A is a valid parentheses string.

You are given a parentheses string s and a string locked, both of length n. locked is a binary string consisting only of '0's and '1's. For each index i of locked,

• If locked[i] is '1', you cannot change s[i].
• But if locked[i] is '0', you can change s[i] to either '(' or ')'.

Return true if you can make s a valid parentheses string. Otherwise, return false.

 

Example 1:

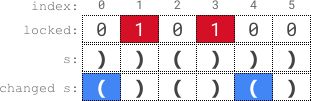
Input: s = "))()))", locked = "010100"
Output: true
Explanation: locked[1] == '1' and locked[3] == '1', so we cannot change s[1] or s[3].
We change s[0] and s[4] to '(' while leaving s[2] and s[5] unchanged to make s valid.

Example 2:

Input: s = "()()", locked = "0000"
Output: true
Explanation: We do not need to make any changes because s is already valid.

Example 3:

Input: s = ")", locked = "0"
Output: false
Explanation: locked permits us to change s[0]. 
Changing s[0] to either '(' or ')' will not make s valid.

Constraints:

• n == s.length == locked.length
• 1 <= n <= 105
• s[i] is either '(' or ')'.
• locked[i] is either '0' or '1'.

class Solution {
    public boolean canBeValid(String s, String locked) {
        //如果不是偶数个，直接返回false
        if(s.length()%2!=0) return false;
        //bal表示待匹配的(个数，chg表示可以改变的个数
        int bal = 0,chg = 0;
        for(int i=0;i<s.length();i++){
            char c = s.charAt(i);
            char lock = locked.charAt(i);
            if(lock=='0'){
                chg++;
            }
            else{
                if(c =='(')
                    bal++;
                else
                    bal--;
            }
            //如果右括弧个数超过了可以改变的个数，那么无法满足
            if(chg+bal<0) return false;
        }
        //bal表示待匹配的)的个数，chg表示可以改变的个数
        chg = 0;
        bal = 0;
        for(int i=s.length()-1;i>=0;i--){
            char c = s.charAt(i);
            char lock = locked.charAt(i);
            if(lock=='0'){
                chg++;
            }
            else{
                if(c ==')')
                    bal++;
                else
                    bal--;
            }
            //如果左括弧个数超过了可以改变的个数，那么无法满足
            if(chg+bal<0) return false;
        }
        return true;
    }
}

   时间复杂度： O(N)

 

22. Generate Parentheses

Medium

13155504Add to ListShare

Given n pairs of parentheses, write a function to generate all combinations of well-formed parentheses.

Example 1:

Input: n = 3
Output: ["((()))","(()())","(())()","()(())","()()()"]

Example 2:

Input: n = 1
Output: ["()"]

Constraints:

• 1 <= n <= 8

解法： 实际就是permutation的过程

class Solution {
    public List<String> generateParenthesis(int n) {
        List<String> result = new ArrayList();
        //dfs 执行permutation
        dfs(n,n,result,"");
        return result;
    }
    public void dfs(int left,int right,List<String> result,String curr){
        if(left<0 || right<0) return;
        if(left==0 && right==0){
            result.add(curr);
            return;
        }
        //永远都是先填充'('才能填充')'
        if(left==right){
            dfs(left-1,right,result,curr+"(");
        }
        else if(left<right){
            dfs(left-1,right,result,curr+"(");
            dfs(left,right-1,result,curr+")");        
        }
    }
}

时间复杂度：O(2ⁿ)

 

1190. Reverse Substrings Between Each Pair of Parentheses

Medium

You are given a string s that consists of lower case English letters and brackets.

Reverse the strings in each pair of matching parentheses, starting from the innermost one.

Your result should not contain any brackets.

 Example 1:

Input: s = "(abcd)"
Output: "dcba"

Example 2:

Input: s = "(u(love)i)"
Output: "iloveu"
Explanation: The substring "love" is reversed first, then the whole string is reversed.

Example 3:

Input: s = "(ed(et(oc))el)"
Output: "leetcode"
Explanation: First, we reverse the substring "oc", then "etco", and finally, the whole string.

Constraints:

• 1 <= s.length <= 2000
• s only contains lower case English characters and parentheses.
• It is guaranteed that all parentheses are balanced.

解法一： bruteforce   O(N²)

class Solution {
    public String reverseParentheses(String s) {
        Stack<Character> stack = new Stack();
        for(int i=0;i<s.length();i++){
            char c = s.charAt(i);
            if(c == ')'){
                LinkedList<Character> list = new LinkedList();
                while(!stack.isEmpty()){
                    char t = stack.pop();
                    if(t=='(') break;
                    else list.add(t);
                }
                while(!list.isEmpty()){
                    stack.push(list.removeFirst());
                }
            }
            else{
                stack.push(c);
            }
        }
        StringBuffer sb = new StringBuffer("");
        for(char c:stack){
            sb.append(c);
        }
        return sb.toString();
    }
}

解法二：O(N)

https://leetcode.com/problems/reverse-substrings-between-each-pair-of-parentheses/discuss/383670/JavaC%2B%2BPython-Tenet-O(N)-Solution#:~:text=Solution%202%3A%20Wormholes

 

2232. Minimize Result by Adding Parentheses to Expression

Medium

You are given a 0-indexed string expression of the form "<num1>+<num2>" where <num1> and <num2> represent positive integers.

Add a pair of parentheses to expression such that after the addition of parentheses, expression is a valid mathematical expression and evaluates to the smallest possible value. The left parenthesis must be added to the left of '+' and the right parenthesis must be added to the right of '+'.

Return expression after adding a pair of parentheses such that expression evaluates to the smallest possible value. If there are multiple answers that yield the same result, return any of them.

The input has been generated such that the original value of expression, and the value of expression after adding any pair of parentheses that meets the requirements fits within a signed 32-bit integer.

 

Example 1:

Input: expression = "247+38"
Output: "2(47+38)"
Explanation: The expression evaluates to 2 * (47 + 38) = 2 * 85 = 170.
Note that "2(4)7+38" is invalid because the right parenthesis must be to the right of the '+'.
It can be shown that 170 is the smallest possible value.

Example 2:

Input: expression = "12+34"
Output: "1(2+3)4"
Explanation: The expression evaluates to 1 * (2 + 3) * 4 = 1 * 5 * 4 = 20.

Example 3:

Input: expression = "999+999"
Output: "(999+999)"
Explanation: The expression evaluates to 999 + 999 = 1998.

Constraints:

• 3 <= expression.length <= 10
• expression consists of digits from '1' to '9' and '+'.
• expression starts and ends with digits.
• expression contains exactly one '+'.
• The original value of expression, and the value of expression after adding any pair of parentheses that meets the requirements fits within a signed 32-bit integer.

class Solution {
    public String minimizeResult(String expression) {
        //因为只会有1个+，所以直接拆两半
        String[] strs = expression.split("\\+");
        String left = strs[0],right = strs[1];
        //先给一个初始值，默认将括号加到左右两侧为最小
        int min = Integer.parseInt(left)+Integer.parseInt(right);
        String result = '('+expression+")";
        //对左侧0～len-1进行轮训尝试
        for(int i=0;i<left.length();i++){
            int leftpre = (i==0) ? 1 : Integer.parseInt(left.substring(0,i));
            int leftpost = Integer.parseInt(left.substring(i));
            //对右侧1～len 进行轮训尝试
            for(int j=1;j<=right.length();j++){
                int rightpre = Integer.parseInt(right.substring(0,j));
                int rightpost = (j==right.length()) ? 1 : Integer.parseInt(right.substring(j));
                //两侧结果结合保留最小值结果
                if(min > leftpre*(leftpost+rightpre)*rightpost ){
                    min = leftpre*(leftpost+rightpre)*rightpost;
                    result = left.substring(0,i)+"("+left.substring(i)+"+"+right.substring(0,j)+")"+right.substring(j);
                }
            }
        }
        return result;
    }
}

 

921. Minimum Add to Make Parentheses Valid

Medium

A parentheses string is valid if and only if:

• It is the empty string,
• It can be written as AB (A concatenated with B), where A and B are valid strings, or
• It can be written as (A), where A is a valid string.

You are given a parentheses string s. In one move, you can insert a parenthesis at any position of the string.

• For example, if s = "()))", you can insert an opening parenthesis to be "(()))" or a closing parenthesis to be "())))".

Return the minimum number of moves required to make s valid.

 Example 1:

Input: s = "())"
Output: 1

Example 2:

Input: s = "((("
Output: 3

Constraints:

• 1 <= s.length <= 1000
• s[i] is either '(' or ')'.

解法：从左向右扫描，记录未被匹配的左右括弧数，加起来即可

 

class Solution {
    public int minAddToMakeValid(String s) {
        int left = 0,right = 0;
        for(int i=0;i<s.length();i++){
            char c = s.charAt(i);
            if(c=='(') left++;//遇到左括弧直接++
            else{
                if(left>0) left--;//如果有待匹配的左括弧，那么左括弧-- 进行抵消
                else right++;//否则，说明没有多余的左括弧，此时未匹配的右括弧需要++
            }
        }
        return left+right;
    }
}

时间复杂度： O(N) 

678. Valid Parenthesis String

Medium

Given a string s containing only three types of characters: '(', ')' and '*', return true if s is valid.

The following rules define a valid string:

• Any left parenthesis '(' must have a corresponding right parenthesis ')'.
• Any right parenthesis ')' must have a corresponding left parenthesis '('.
• Left parenthesis '(' must go before the corresponding right parenthesis ')'.
• '*' could be treated as a single right parenthesis ')' or a single left parenthesis '(' or an empty string "".

Example 1:

Input: s = "()"
Output: true

Example 2:

Input: s = "(*)"
Output: true

Example 3:

Input: s = "(*))"
Output: true

Constraints:

• 1 <= s.length <= 100
• s[i] is '(', ')' or '*'.

class Solution {
    public boolean checkValidString(String s) {
        Stack<Integer> stack1 = new Stack<>();
        Stack<Integer> stack2 = new Stack<>();
        for(int i = 0; i < s.length(); i++) {
            char c = s.charAt(i);
            if(c == '*' ) stack2.push(i);
            else if(c == '(') stack1.push(i);
            else {
                if(!stack1.isEmpty()) stack1.pop();
                else {
                    if(!stack2.isEmpty()) stack2.pop();
                    else return false;
                }
            }
        }
        while(!stack1.isEmpty()) {
            if(stack2.isEmpty() || stack1.peek() > stack2.peek()) return false;
            stack1.pop();
            stack2.pop();
        }
        return true;
    }
}

 

 

class Solution {
    public boolean checkValidString(String s) {
        int min = 0;//表示最大未匹配的左括号个数，当我们把所有的*当作')'
        int max = 0;//表示最小未匹配的左括号个数，当我们把所有的*当作'('
        for(int i=0;i<s.length();i++){
            char c = s.charAt(i);
            if(c=='('){
                min++;
                max++;
            }
            else if(c==')'){
                min--;
                max--;
            }
            else{
                min--;
                max++;
            }
            //如果把可能的*全部都当‘(’来看，‘(’都不够的话，那就没辙了
            if(max<0){
                return false;
            }
            //上面条件没false，说明右括弧没有多，那么把*变成左括弧还是可以补救的.
            if(min<0){
                min = 0;
            }
        }
        return min ==0;
    }
}

241. Different Ways to Add Parentheses

Medium

Given a string expression of numbers and operators, return all possible results from computing all the different possible ways to group numbers and operators. You may return the answer in any order.

Example 1:

Input: expression = "2-1-1"
Output: [0,2]
Explanation:
((2-1)-1) = 0 
(2-(1-1)) = 2

Example 2:

Input: expression = "2*3-4*5"
Output: [-34,-14,-10,-10,10]
Explanation:
(2*(3-(4*5))) = -34 
((2*3)-(4*5)) = -14 
((2*(3-4))*5) = -10 
(2*((3-4)*5)) = -10 
(((2*3)-4)*5) = 10

Constraints:

• 1 <= expression.length <= 20
• expression consists of digits and the operator '+', '-', and '*'.
• All the integer values in the input expression are in the range [0, 99].

解法：分治法

每次找运算符号对左右两侧进行切分

终止条件：字符串中没有运算符

class Solution {
    public List<Integer> diffWaysToCompute(String expression) {
        //定义当前表达式返回集合
        List<Integer> result = new ArrayList();
        for(int i=0; i<expression.length(); i++){
            char c = expression.charAt(i);
            //如果遇到运算符，则分别对运算符左右两侧进行dfs
            if( c=='+' || c=='-' || c=='*'){
                List<Integer> pre = diffWaysToCompute(expression.substring(0,i));
                List<Integer> post = diffWaysToCompute(expression.substring(i+1));
                //将左右两侧子表达式的运算结果进行配对
                for(int preItem:pre){
                    for(int postItem:post){
                        if(c=='+') result.add(preItem + postItem);
                        else if(c=='-') result.add(preItem - postItem);
                        else if(c=='*') result.add(preItem * postItem);                        
                    }
                }
            }
        }
        //如果result是空的说明当前是个纯数字无表达式
        if(result.isEmpty()) result.add(Integer.valueOf(expression));
        return result;
    }
}

 

856. Score of Parentheses

Medium

Given a balanced parentheses string s, return the score of the string.

The score of a balanced parentheses string is based on the following rule:

• "()" has score 1.
• AB has score A + B, where A and B are balanced parentheses strings.
• (A) has score 2 * A, where A is a balanced parentheses string. 

Example 1:

Input: s = "()"
Output: 1

Example 2:

Input: s = "(())"
Output: 2

Example 3:

Input: s = "()()"
Output: 2

Constraints:

• 2 <= s.length <= 50
• s consists of only '(' and ')'.
• s is a balanced parentheses string.

class Solution {
    public int scoreOfParentheses(String s) {
        Stack<String> stack = new Stack();
        for(int i=0;i<s.length();i++){
            char c = s.charAt(i);
            //遇到左括弧push
            if(c=='('){
                stack.push(c+"");
            }
            //遇到右括弧
            else{
                int temp = 0;
                //先看是不是有数字，有数字的话先都pop出来加起来，直到出现（
                while(!stack.isEmpty() && !"(".equals(stack.peek())){
                    temp += Integer.parseInt(stack.pop());
                }
                //pop出（
                stack.pop();
                //如果没有嵌套 就是1，如果有嵌套 就是嵌套值*2
                int result = (temp==0) ? 1: temp*2;
                stack.push(""+result);
            }
        }
        int sum = 0;
        for(String curr:stack) sum+=Integer.parseInt(curr);
        return sum;
    }
}

301. Remove Invalid Parentheses

Hard

4710238Add to ListShare

Given a string s that contains parentheses and letters, remove the minimum number of invalid parentheses to make the input string valid.

Return all the possible results. You may return the answer in any order.

 

Example 1:

Input: s = "()())()"
Output: ["(())()","()()()"]

Example 2:

Input: s = "(a)())()"
Output: ["(a())()","(a)()()"]

Example 3:

Input: s = ")("
Output: [""]

Constraints:

• 1 <= s.length <= 25
• s consists of lowercase English letters and parentheses '(' and ')'.
• There will be at most 20 parentheses in s.

class Solution {
    public List<String> removeInvalidParentheses(String s) {
        List<String> result = new ArrayList();
        //1.check how many left/right need to delete
        int left = 0,right = 0;
        for(char c:s.toCharArray()){
            if(c=='(') left++;
            else if(c==')'){
                if(left>0) left--;
                else right++;
            }
        }
        //2.dfs try every possibility
        dfs(new StringBuffer(s), left, right, 0, result);
        return result;
    }
    public void dfs(StringBuffer s, int left, int right, int ind, List<String> result){
        if(left == 0 && right == 0){
            if(valid(s.toString())) result.add(s.toString());
            return;
        }
        for(int i=ind;i<s.length();i++){
            char c = s.charAt(i);
            if(i>ind && s.charAt(i) == s.charAt(i-1)) continue;
            if(left>0 && c=='('){
                dfs(new StringBuffer(s).delete(i,i+1), left-1, right, i, result);
            }
            if(right>0 && c==')'){
                dfs(new StringBuffer(s).delete(i,i+1), left, right-1, i, result);
            }
        }
    }
    public boolean valid(String s){
        int left = 0;
        int right = 0;
        for(char c: s.toCharArray()){
            if(c == '(') left++;
            else if(c ==')'){
                if(left>0) left--;
                else 
                    return false;
            }
        }
        return left==0;
    }
}