题解 P10107【[GDKOI2023 提高组] 树】

$\text{Link}$

相当巧妙的倍增/差分题。

题意

给你一颗 $n$ 个结点的树，点有点权，$q$ 次询问给出 $x,k$，求：

$$\sum_uv_u\oplus d(u,x)$$

其中 $u$ 为 $x$ 子树中距离 $x$ 不超过 $k$ 的所有点，$d(x,y)$ 为 $x$ 到 $y$ 的距离。

$n,q\le 10^6$.

思路

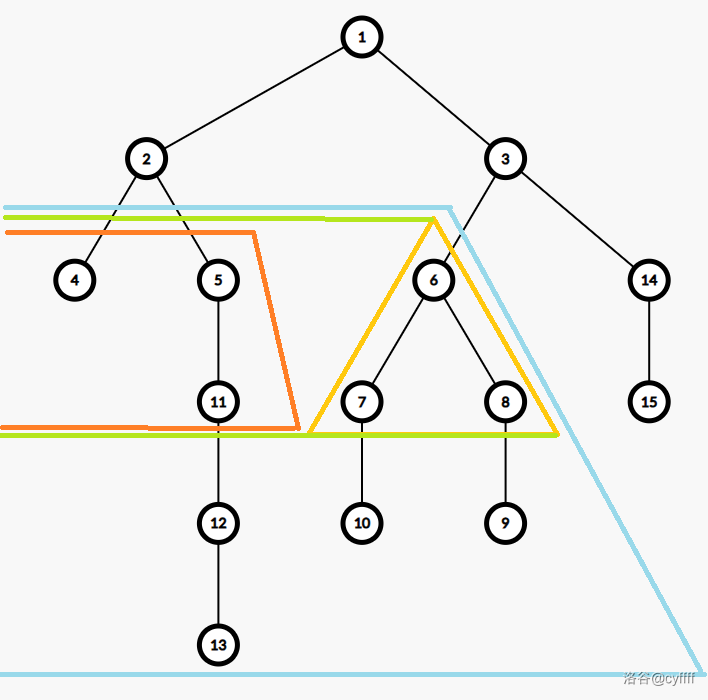
考虑这样一颗树，要求 $6$ 子树中距离它不超过 $1$ 的点的答案，即黄色部分。我们可以用绿色部分的答案减去橙色部分的答案得到黄色部分的答案（由于深度相同可以直接减）。

定义一个结点 $x$ 对应的蓝色区域为所有深度 $\ge dep_x$ 的点中 $dfn$ 小于等于 $low_x$ 的结点。如上图中给出了结点 $6$ 对应的蓝色区域。

定义一个结点 $x$ 对应的深度为 $k$ 的绿色区域为所有深度在 $[dep_x,dep_x+k)$ 中的点中 $dfn$ 小于等于 $low_x$ 的结点。如上图中给出了结点 $6$ 对应的深度为 $2$ 的绿色区域。

那么不妨对于每个深度的结点按 $\text{dfs}$ 序排序，记 $pr_x$ 为 $x$ 在深度为 $dep_x$ 的点中的前驱，$rs_x$ 为 $x$ 子树中 $\text{dfs}$ 序最大的子结点（没有子结点则设为 $rs_{pr_x}$）。

考虑到所求的值中有深度相关的异或运算，需要利用有二进制相关性质的维护方式，不妨考虑使用倍增。记 $rs_{i,x}$ 表示对 $x$ 进行 $2^i$ 次 $x\gets rs_x$ 得到的结点，$f_{i,x}$ 为 $x$ 对应的深度为 $2^i$ 的绿色区域的答案。

考虑从 $f_{i-1,x}\to f_{i,x}$，$rs_{i-1,x}$ 的深度为 $2^{i-1}$ 的绿色区域中所有点的点权都要异或上 $2^{i-1}$，于是还需要维护 $cnt_x$ 表示 $x$ 对应的蓝色区域的结点数，$vnt_{i,x}$ 表示 $x$ 对应的蓝色区域中有几个点的点权第 $i$ 位为 $1$。用 $vnt_{i-1,rs_{i-1,x}}$ 减去 $vnt_{i-1,rs_{i,x}}$ 就可以得到有几个数的第 $i-1$ 位会从 $1$ 变成 $0$，同理可求有几个数此位从 $0$ 变成 $1$。

询问时用 $x$ 的深度为 $k$ 的绿色区域的答案减去 $pr_x$ 的即可，考虑求 $x$ 的答案，先求出 $p$ 为 $x$ 进行 $k$ 次 $x\gets rs_x$ 得到的结点，然后每次从 $x$ 跳 $2^i$ 步到 $rs_{i,x}$ 时，$rs_{i,x}$ 的蓝色区域减去 $p$ 的蓝色区域内的点权的第 $i$ 位都会改变，同上求出即可。

时间复杂度 $O(n\log n)$。

代码：

#include<bits/stdc++.h>
using namespace std;
#define ll long long
namespace IO{//by cyffff

}
const int N=1e6+10,L=20;
int n,q,dep[N],v[N],pr[N],rs[L][N],cnt[N],vnt[L][N];
ll f[L][N];
vector<int>a[N],vec[N];
inline void dfs1(int x){
    vec[dep[x]].push_back(x);
    for(auto t:a[x])
        rs[0][x]=t,dep[t]=dep[x]+1,dfs1(t);
}
inline void dfs2(int x){
    for(auto t:a[x])
        dfs2(t);
    cnt[x]+=cnt[rs[0][x]];
    for(int k=0;k<L;k++)
        vnt[k][x]+=vnt[k][rs[0][x]];
}
inline ll solve(int x,int k){
    if(!x) return 0;
    k++;
    int p=x;
    ll ans=0;
    for(int i=L-1;i>=0;i--)
        if(k>>i&1)
            ans+=f[i][p],p=rs[i][p];
    for(int i=L-1;i>=0;i--)
        if(k>>i&1){
            int t=rs[i][x];
            int c0=vnt[i][t]-vnt[i][p];
            int c1=cnt[t]-cnt[p]-c0;
            ans+=(c1-c0)*(1ll<<i);
            x=t;
        }
    return ans;
}
int main(){
    n=read();
    for(int i=1;i<=n;i++)
        v[i]=read();
    for(int i=2;i<=n;i++)
        a[read()].push_back(i);
    dfs1(1);
    for(int i=0;i<=n;i++){
        if(!vec[i].size()) break;
        for(int j=0;j<vec[i].size();j++){
            int x=vec[i][j];
            if(j) pr[x]=vec[i][j-1];
            if(!rs[0][x]) rs[0][x]=rs[0][pr[x]];
            f[0][x]=v[x]+f[0][pr[x]];
            cnt[x]=1+cnt[pr[x]];
            for(int k=0;k<L;k++)
                vnt[k][x]=(v[x]>>k&1)+vnt[k][pr[x]];
        }
    }
    dfs2(1);
    for(int i=1;i<L;i++)
        for(int x=1;x<=n;x++){
            rs[i][x]=rs[i-1][rs[i-1][x]];
            int t=rs[i-1][x],p=rs[i][x];
            int c0=vnt[i-1][t]-vnt[i-1][p];
            int c1=cnt[t]-cnt[p]-c0;
            f[i][x]=f[i-1][x]+f[i-1][t]+(c1-c0)*(1ll<<i-1);
        }
    q=read();
    while(q--){
        int x=read(),k=read();
        write(solve(x,k)-solve(pr[x],k)),putc('\n');
    }
    flush();
}