动态规划算法之0-1背包问题
一、问题描述:有n 个物品,它们有各自的重量和价值,现有给定容量的背包,如何让背包里装入的物品具有最大的价值总和?
二、总体思路:根据动态规划解题步骤(问题抽象化、建立模型、寻找约束条件、判断是否满足最优性原理、找大问题与小问题的递推关系式、填表、寻找解组成)找出01背包问题的最优解以及解组成;
三、动态规划的原理及过程:
eg:number=4,capacity=8
|
i |
1 |
2 |
3 |
4 |
|
w(体积) |
2 |
3 |
4 |
5 |
|
v(价值) |
3 |
4 |
5 |
6 |
1、原理
动态规划与分治法类似,都是把大问题拆分成小问题,通过寻找大问题与小问题的递推关系,解决一个个小问题,最终达到解决原问题的效果。但不同的是,分治法在子问题和子子问题等上被重复计算了很多次,而动态规划则具有记忆性,通过填写表把所有已经解决的子问题答案纪录下来,在新问题里需要用到的子问题可以直接提取,避免了重复计算,从而节约了时间,所以在问题满足最优性原理之后,用动态规划解决问题的核心就在于填表,表填写完毕,最优解也就找到。
2、过程
a) 把背包问题抽象化(X1,X2,…,Xn,其中 Xi 取0或1,表示第 i 个物品选或不选),Vi表示第 i 个物品的价值,Wi表示第 i 个物品的体积(重量);
b) 建立模型,即求max(V1X1+V2X2+…+VnXn);
c) 约束条件,W1X1+W2X2+…+WnXn<capacity;
d) 定义V(i,j):当前背包容量 j,前 i 个物品最佳组合对应的价值;
e) 最优性原理是动态规划的基础,最优性原理是指“多阶段决策过程的最优决策序列具有这样的性质:不论初始状态和初始决策如何,对于前面决策所造成的某一状态而言,其后各阶段的决策序列必须构成最优策略”。判断该问题是否满足最优性原理,采用反证法证明:
假设(X1,X2,…,Xn)是01背包问题的最优解,则有(X2,X3,…,Xn)是其子问题的最优解,
假设(Y2,Y3,…,Yn)是上述问题的子问题最优解,则理应有(V2Y2+V3Y3+…+VnYn)+V1X1 > (V2X2+V3X3+…+VnXn)+V1X1;
而(V2X2+V3X3+…+VnXn)+V1X1=(V1X1+V2X2+…+VnXn),则有(V2Y2+V3Y3+…+VnYn)+V1X1 > (V1X1+V2X2+…+VnXn);
该式子说明(X1,Y2,Y3,…,Yn)才是该01背包问题的最优解,这与最开始的假设(X1,X2,…,Xn)是01背包问题的最优解相矛盾,故01背包问题满足最优性原理;
f) 寻找递推关系式,面对当前商品有两种可能性:
第一,包的容量比该商品体积小,装不下,此时的价值与前i-1个的价值是一样的,即V(i,j)=V(i-1,j);
第二,还有足够的容量可以装该商品,但装了也不一定达到当前最优价值,所以在装与不装之间选择最优的一个,即V(i,j)=max{ V(i-1,j),V(i-1,j-w(i))+v(i) }
其中V(i-1,j)表示不装,V(i-1,j-w(i))+v(i) 表示装了第i个商品,背包容量减少w(i)但价值增加了v(i);
由此可以得出递推关系式:
1) j<w(i) V(i,j)=V(i-1,j)
2) j>=w(i) V(i,j)=max{ V(i-1,j),V(i-1,j-w(i))+v(i) }
g) 填表,首先初始化边界条件,V(0,j)=V(i,0)=0;

h) 然后一行一行的填表,
1) 如,i=1,j=1,w(1)=2,v(1)=3,有j<w(1),故V(1,1)=V(1-1,1)=0;
2) 又如i=1,j=2,w(1)=2,v(1)=3,有j=w(1),故V(1,2)=max{ V(1-1,2),V(1-1,2-w(1))+v(1) }=max{0,0+3}=3;
3) 如此下去,填到最后一个,i=4,j=8,w(4)=5,v(4)=6,有j>w(4),故V(4,8)=max{ V(4-1,8),V(4-1,8-w(4))+v(4) }=max{9,4+6}=10;所以填完表如下图:

i) 表格填完,最优解即是V(number,capacity)=V(4,8)=10,但还不知道解由哪些商品组成,故要根据最优解回溯找出解的组成,根据填表的原理可以有如下的寻解方式:
1) V(i,j)=V(i-1,j)时,说明没有选择第i 个商品,则回到V(i-1,j);
2) V(i,j)=V(i-1,j-w(i))+v(i)实时,说明装了第i个商品,该商品是最优解组成的一部分,随后我们得回到装该商品之前,即回到V(i-1,j-w(i));
3) 一直遍历到i=0结束为止,所有解的组成都会找到。
j) 如上例子,
1) 最优解为V(4,8)=10,而V(4,8)!=V(3,8)却有V(4,8)=V(3,8-w(4))+v(4)=V(3,3)+6=4+6=10,所以第4件商品被选中,并且回到V(3,8-w(4))=V(3,3);
2) 有V(3,3)=V(2,3)=4,所以第3件商品没被选择,回到V(2,3);
3) 而V(2,3)!=V(1,3)却有V(2,3)=V(1,3-w(2))+v(2)=V(1,0)+4=0+4=4,所以第2件商品被选中,并且回到V(1,3-w(2))=V(1,0);
4) 有V(1,0)=V(0,0)=0,所以第1件商品没被选择;

k) 到此,01背包问题已经解决,利用动态规划解决此问题的效率即是填写此张表的效率,所以动态规划的时间效率为O(number*capacity)=O(n*c),由于用到二维数组存储子问题的解,所以动态规划的空间效率为O(n*c);
L)程序实现:

import java.util.Scanner; public class Main { public static void zeroOnePack(){ Scanner scanner = new Scanner(System.in); String packInfo = null; String weights = null; String values = null; while(scanner.hasNextLine()){ packInfo = scanner.nextLine(); int packageWeight = Integer.valueOf(packInfo.split(" ")[0]); int numbers = Integer.valueOf(packInfo.split(" ")[1]); weights = scanner.nextLine(); values = scanner.nextLine(); String[] weis = weights.split(" "); String[] vals = values.split(" "); //weight[]数组是从下标0开始存储,索引0存储第一件物品的重量 int[] weight = new int[numbers]; int[] value = new int[numbers]; for(int i = 0; i < numbers; i++) { weight[i] = Integer.valueOf(weis[i]); value[i] = Integer.valueOf(vals[i]); } int[][] dp = new int[numbers + 1][packageWeight + 1]; //init for(int i = 0; i <= numbers; i++) dp[i][0] = 0; for(int i = 0; i <= packageWeight; i++) dp[0][i] = 0; //dp[i][j] = max{dp[i-1][j], dp[i-1][j-weight[i-1]]+value[i-1]} for(int i = 1; i <= numbers; i++) { for(int j = 1; j <= packageWeight; j++) { if(weight[i-1] > j)// 第i件物品的重量大于背包的承重 { dp[i][j] = dp[i-1][j]; continue; } //dp[i][j] = max{dp[i-1][j], dp[i-1][j-weight[i-1]]+value[i-1]} if(dp[i-1][j] < dp[i-1][j-weight[i-1]] + value[i-1]) dp[i][j] = dp[i-1][j-weight[i-1]] + value[i-1]; else dp[i][j] = dp[i-1][j]; } } System.out.println(dp[numbers][packageWeight]);//输出背包能够装的最大价值 //反向找出 选中的物品(哪些物品装入到背包中了?) int j= packageWeight; for(int i = numbers;i>0;i--){ if(dp[i][j]>dp[i-1][j]){ System.out.print(i+" ");//输出选中的物品的编号 j=j-weight[i-1]; if(j<0) break; } }//end while } scanner.close(); } // test case //10 5 //2 2 6 5 4 //6 3 5 4 6 public static void main(String[] args) { zeroOnePack(); } }
M)运行结果:
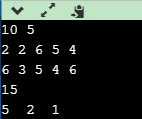
由结果可知,最大价值是15,选取的物品是第1,2,5件
参考文献:王晓东《算法设计与分析》
https://www.cnblogs.com/hapjin/p/5818418.html
https://www.cnblogs.com/Christal-R/p/Dynamic_programming.html(总结的很好)





 浙公网安备 33010602011771号
浙公网安备 33010602011771号