P5465
# [P5465[PKUSC2018]星际穿越](https://www.luogu.com.cn/problem/P5465)
一道倍增好题。
建议先把 [P4155 [SCOI2015]国旗计划](https://www.luogu.com.cn/problem/P4155) 做掉,并理解 LCA 的倍增方法和 ST 表的倍增方法,此题是二者的结合 ~~不然为什么是紫的~~。
先读题,首先给出一个数组 $L_x , x \in [2, n]$,对每一个 $ver_i \in [L_x, x]$,都会和 $ver_x$ 连一条双向边。给出 $m$ 次询问,求 $\sum_{y = l_i}^{r_i}dist(x,y)/(r_i - l_i + 1)$。
接着读样例
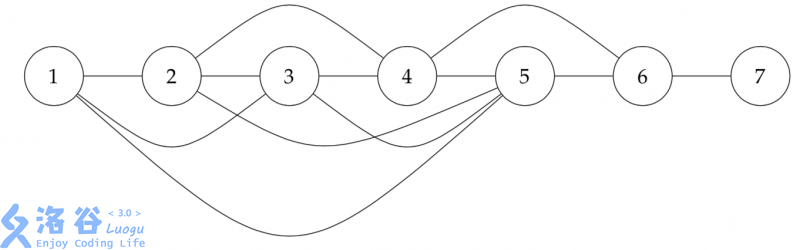
实质上是在求 $ver_x$ 到 $ver_{l_i} \sim ver_{r_i}$ 的最短距离和
最后看一眼数据范围 $n,q \le 3\cdot 10^5$
可以猜出复杂度大致为 $O(q \log n)$。
## ~~我会暴力~~
对每次询问都进行计算 $\sum_{y = l_i}^{r_i}dist(x,y)$。
## 我会观察性质
手动模拟一下走法,可以发现 $dist(x,i)$ 随着 $i$ 的增大而不降。
## 我会优化
在文章的开头已经提到了这是一道倍增题,接下来就是如何使用倍增优化上述的算法。
首先我们观察到题目问的是 $l_i \sim r_i$ 的距离之和,很自然就会想到前缀和优化来快速计算,然而如果要存下这个 $sum$ 无论是在空间还是时间上都是无法接受的。
但是我们还有性质,观察如下的一列数
$$dist_x = \{4,4,4,4,4,3,3,3,3,2,2,2,2,2,2,1,1,1,0 \}$$
我们有两个问题,第一,这列数如何生成,第二,这列数有什么用。
### 如何计算 $dist$
设 $y_{x,i}$ 表示以 $ver_x$ 为起点,$dist_y$ 为 $i$ 的最小的 $y$。
$$\begin{cases}
y_{x,0} = L_x \\
y_{x,1} = \min \{ L_{y_{x,0}}, \cdots L_n \}\\
\vdots
\end{cases}$$
关于为何 $\min$ 右边界为 $L_n$,其他题解已经解释得比较明白了,就不再赘述。
### $dist$ 有什么用
实际上这个算法的复杂度为 $O(n^2)$ 不足以通过此题,考虑优化。
~~都说了这是倍增题~~可以尝试优化为倍增。
设 $pre_{x,i}$ 为 $ver_x$ 左边 $dist_y$ 为 $2^i$ 的最左侧节点。
所以有
$$pre_{n,0} = L_n$$
$$pre_{i,0} = \min_i^n \{L_y\}$$
$$pre_{i,j} = pre_{pre_{i,j - 1},j - 1}$$
这样我们就可以使用倍增法来快速计算 $sum$ 了。
令 $sum_{i,j}$ 为以 $ver_i$ 为起点,左端点值为 $2^j$ 的前缀和
则有
$$sum_{i,0} = i - pre_{i,0}$$
$$sum_{i,j} = sum_{i,j - 1} + sum_{pre_{i,j - 1},j - 1} + 2 ^ {i - 1}\cdot(pre_{i,j - 1} - pre_{i,j})$$
那么最终倍增求解的前缀和便是:
$$S = S + sum_{p,i} + cnt \cdot (p - pre_{p,i})$$
最终复杂度为 $O((n+q)\log n)$。
## 一些细节
此题在计算时由于第一步在走出时不一定会向左边走,故需单独计算。
**不要忘记本题需要约分**。
## code
```cpp
// coding by cxz_0
#include <bits/stdc++.h>
#define awa cerr << "xlx is my superman!!!!!!!!!!!\n";
#define FOR(x,l,r) for(int (x) = (l); (x) <= (r); (x)++)
#define _FOR(x,l,r) for(int (x) = (r); (x) >= (l); (x)--)
#define gc getchar()
#define pb emplace_back
#define mp make_pair
#define pii pair<int, int >
#define PII pair<ll, ll >
#define fi first
#define se second
#define p_q priority_queue
// #define int ll
#define il inline
using namespace std;
typedef long long ll;
const int N = 3e5 + 5,MOD = 1e9 + 7;
int n, m, a[N], pre[N][20];
ll sum[N][20];
namespace cxz_0
{
il int read(int x=0,bool f=0,char c=gc){while(!isdigit(c))f=c=='-',c=gc;while(isdigit(c))x=(x<<1)+(x<<3)+(c^48),c=gc;return f?-x:x;}
il void write(int x){if(x<0)x=-x,putchar('-');if(x>9)write(x/10);putchar(x%10+'0');}
il ll readl(ll x=0,bool f=0,char c=gc){while(!isdigit(c))f=c=='-',c=gc;while(isdigit(c))x=(x<<1)+(x<<3)+(c^48),c=gc;return f?-x:x;}
il void writel(ll x){if(x<0)x=-x,putchar('-');if(x>9)writel(x/10);putchar(x%10+'0');}
il int qpow(int a, int n, int p){int b=1;while(n){if(n&1)b=1ll*b*a%p;a=1ll*a*a%p;n>>=1;}return b;}
il int max(int&a,int&b){return a>b?a:b;}
il int min(int&a,int&b){return a<b?a:b;}
il void swap(int&a,int&b){a^=b^=a^=b;}
il int Mod(int x){return x>MOD?Mod(x-MOD):x;}
} using namespace cxz_0;
il ll cal (int fr, int to)
{
if (a[fr] <= to) return fr - to;
ll S = fr - a[fr];
int cnt = 1;
fr = a[fr];
_FOR (i, 0, 19) if (pre[fr][i] >= to)
{
S += cnt * (fr - pre[fr][i]) + sum[fr][i];
cnt += (1 << i);
fr = pre[fr][i];
}
if (fr > to) S += cnt * (fr - to) + fr - to;
return S;
}
signed main()
{
#ifndef ONLINE_JUDGE
double start = clock();
freopen("test.in", "r", stdin);
freopen("test.out", "w", stdout);
#endif
n = read ();
FOR (i, 2, n) a[i] = read ();
int mi = a[n];
pre[n][0] = a[n], sum[n][0] = n - a[n];
_FOR (i, 1, n - 1) mi = min (mi, a[i]), pre[i][0] = mi, sum[i][0] = i - mi;
FOR (j, 1, 19) FOR (i, 1, n) pre[i][j] = pre[pre[i][j - 1]][j - 1];
FOR (j, 1, 19) FOR (i, 1, n) sum[i][j] = sum[i][j - 1] + sum[pre[i][j - 1]][j - 1] + (1 << (j - 1)) * (pre[i][j - 1] - pre[i][j]);
m = read ();
while (m--)
{
int l = read (), r = read (), x = read ();
ll c = cal (x, l) - cal (x, r + 1), d = r - l + 1, g = __gcd (c, d);
writel (c / g);
putchar (47);
writel (d / g);
putchar (10);
}
#ifndef ONLINE_JUDGE
cerr << "Time: " << 1e3 * (clock() - start) / CLOCKS_PER_SEC << " ms" << endl;
awa
#endif
return 0;
}
```
一道倍增好题。
建议先把 [P4155 [SCOI2015]国旗计划](https://www.luogu.com.cn/problem/P4155) 做掉,并理解 LCA 的倍增方法和 ST 表的倍增方法,此题是二者的结合 ~~不然为什么是紫的~~。
先读题,首先给出一个数组 $L_x , x \in [2, n]$,对每一个 $ver_i \in [L_x, x]$,都会和 $ver_x$ 连一条双向边。给出 $m$ 次询问,求 $\sum_{y = l_i}^{r_i}dist(x,y)/(r_i - l_i + 1)$。
接着读样例

实质上是在求 $ver_x$ 到 $ver_{l_i} \sim ver_{r_i}$ 的最短距离和
最后看一眼数据范围 $n,q \le 3\cdot 10^5$
可以猜出复杂度大致为 $O(q \log n)$。
## ~~我会暴力~~
对每次询问都进行计算 $\sum_{y = l_i}^{r_i}dist(x,y)$。
## 我会观察性质
手动模拟一下走法,可以发现 $dist(x,i)$ 随着 $i$ 的增大而不降。
## 我会优化
在文章的开头已经提到了这是一道倍增题,接下来就是如何使用倍增优化上述的算法。
首先我们观察到题目问的是 $l_i \sim r_i$ 的距离之和,很自然就会想到前缀和优化来快速计算,然而如果要存下这个 $sum$ 无论是在空间还是时间上都是无法接受的。
但是我们还有性质,观察如下的一列数
$$dist_x = \{4,4,4,4,4,3,3,3,3,2,2,2,2,2,2,1,1,1,0 \}$$
我们有两个问题,第一,这列数如何生成,第二,这列数有什么用。
### 如何计算 $dist$
设 $y_{x,i}$ 表示以 $ver_x$ 为起点,$dist_y$ 为 $i$ 的最小的 $y$。
$$\begin{cases}
y_{x,0} = L_x \\
y_{x,1} = \min \{ L_{y_{x,0}}, \cdots L_n \}\\
\vdots
\end{cases}$$
关于为何 $\min$ 右边界为 $L_n$,其他题解已经解释得比较明白了,就不再赘述。
### $dist$ 有什么用
实际上这个算法的复杂度为 $O(n^2)$ 不足以通过此题,考虑优化。
~~都说了这是倍增题~~可以尝试优化为倍增。
设 $pre_{x,i}$ 为 $ver_x$ 左边 $dist_y$ 为 $2^i$ 的最左侧节点。
所以有
$$pre_{n,0} = L_n$$
$$pre_{i,0} = \min_i^n \{L_y\}$$
$$pre_{i,j} = pre_{pre_{i,j - 1},j - 1}$$
这样我们就可以使用倍增法来快速计算 $sum$ 了。
令 $sum_{i,j}$ 为以 $ver_i$ 为起点,左端点值为 $2^j$ 的前缀和
则有
$$sum_{i,0} = i - pre_{i,0}$$
$$sum_{i,j} = sum_{i,j - 1} + sum_{pre_{i,j - 1},j - 1} + 2 ^ {i - 1}\cdot(pre_{i,j - 1} - pre_{i,j})$$
那么最终倍增求解的前缀和便是:
$$S = S + sum_{p,i} + cnt \cdot (p - pre_{p,i})$$
最终复杂度为 $O((n+q)\log n)$。
## 一些细节
此题在计算时由于第一步在走出时不一定会向左边走,故需单独计算。
**不要忘记本题需要约分**。
## code
```cpp
// coding by cxz_0
#include <bits/stdc++.h>
#define awa cerr << "xlx is my superman!!!!!!!!!!!\n";
#define FOR(x,l,r) for(int (x) = (l); (x) <= (r); (x)++)
#define _FOR(x,l,r) for(int (x) = (r); (x) >= (l); (x)--)
#define gc getchar()
#define pb emplace_back
#define mp make_pair
#define pii pair<int, int >
#define PII pair<ll, ll >
#define fi first
#define se second
#define p_q priority_queue
// #define int ll
#define il inline
using namespace std;
typedef long long ll;
const int N = 3e5 + 5,MOD = 1e9 + 7;
int n, m, a[N], pre[N][20];
ll sum[N][20];
namespace cxz_0
{
il int read(int x=0,bool f=0,char c=gc){while(!isdigit(c))f=c=='-',c=gc;while(isdigit(c))x=(x<<1)+(x<<3)+(c^48),c=gc;return f?-x:x;}
il void write(int x){if(x<0)x=-x,putchar('-');if(x>9)write(x/10);putchar(x%10+'0');}
il ll readl(ll x=0,bool f=0,char c=gc){while(!isdigit(c))f=c=='-',c=gc;while(isdigit(c))x=(x<<1)+(x<<3)+(c^48),c=gc;return f?-x:x;}
il void writel(ll x){if(x<0)x=-x,putchar('-');if(x>9)writel(x/10);putchar(x%10+'0');}
il int qpow(int a, int n, int p){int b=1;while(n){if(n&1)b=1ll*b*a%p;a=1ll*a*a%p;n>>=1;}return b;}
il int max(int&a,int&b){return a>b?a:b;}
il int min(int&a,int&b){return a<b?a:b;}
il void swap(int&a,int&b){a^=b^=a^=b;}
il int Mod(int x){return x>MOD?Mod(x-MOD):x;}
} using namespace cxz_0;
il ll cal (int fr, int to)
{
if (a[fr] <= to) return fr - to;
ll S = fr - a[fr];
int cnt = 1;
fr = a[fr];
_FOR (i, 0, 19) if (pre[fr][i] >= to)
{
S += cnt * (fr - pre[fr][i]) + sum[fr][i];
cnt += (1 << i);
fr = pre[fr][i];
}
if (fr > to) S += cnt * (fr - to) + fr - to;
return S;
}
signed main()
{
#ifndef ONLINE_JUDGE
double start = clock();
freopen("test.in", "r", stdin);
freopen("test.out", "w", stdout);
#endif
n = read ();
FOR (i, 2, n) a[i] = read ();
int mi = a[n];
pre[n][0] = a[n], sum[n][0] = n - a[n];
_FOR (i, 1, n - 1) mi = min (mi, a[i]), pre[i][0] = mi, sum[i][0] = i - mi;
FOR (j, 1, 19) FOR (i, 1, n) pre[i][j] = pre[pre[i][j - 1]][j - 1];
FOR (j, 1, 19) FOR (i, 1, n) sum[i][j] = sum[i][j - 1] + sum[pre[i][j - 1]][j - 1] + (1 << (j - 1)) * (pre[i][j - 1] - pre[i][j]);
m = read ();
while (m--)
{
int l = read (), r = read (), x = read ();
ll c = cal (x, l) - cal (x, r + 1), d = r - l + 1, g = __gcd (c, d);
writel (c / g);
putchar (47);
writel (d / g);
putchar (10);
}
#ifndef ONLINE_JUDGE
cerr << "Time: " << 1e3 * (clock() - start) / CLOCKS_PER_SEC << " ms" << endl;
awa
#endif
return 0;
}
```


 浙公网安备 33010602011771号
浙公网安备 33010602011771号