n皇后问题

学过dfs了，八皇后问题在学的时候打过一遍，想看看忘记了没有。果然学过，打过，ac了之后依然还是有细节没注意到

一定要细心，d[N]和ud[N],打错了ud打成d调了一个小时

---

思路：因为每行每列每条对角线都最多有一个皇后，这样我只在每一行放一个皇后，枚举在这一行的那一列放皇后，判断一下这一列和当前行列对应的两条对角线是否能放皇后，那么问题就转化为我们如何判断这一列和当前对角线是否能放皇后。

这里我们用三个数组r[N], d[N], ud[N]，三个数组来表示列，一条对角线，和另一条对角线

对于对角线如何表示

---

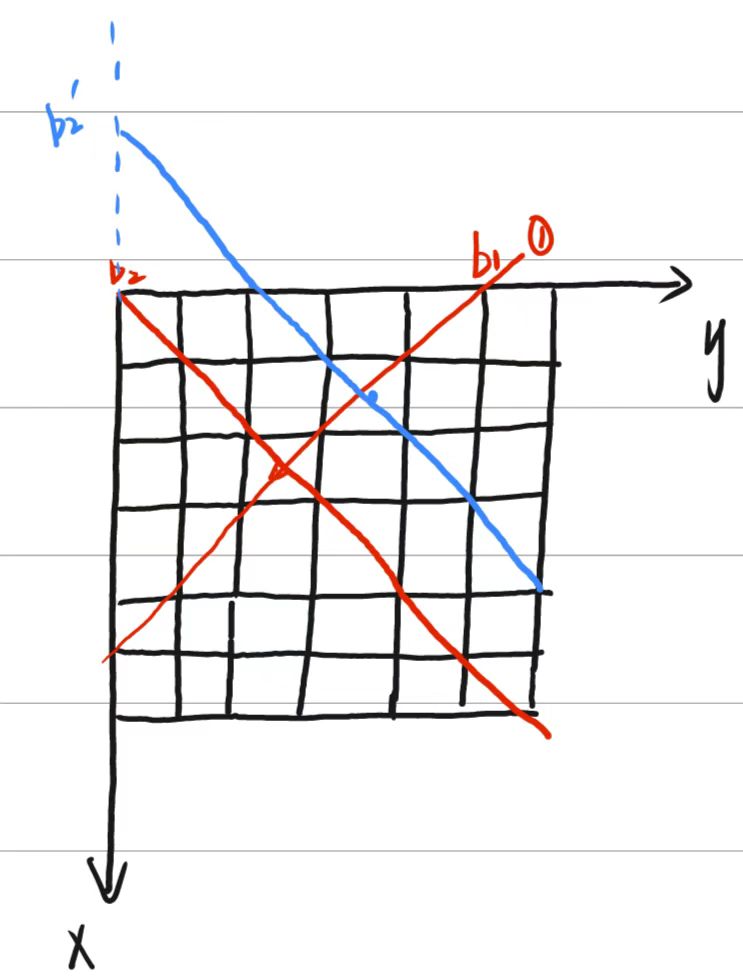
[USACO1.5]八皇后 Checker Challenge

题目描述

一个如下的 \(6 \times 6\) 的跳棋棋盘，有六个棋子被放置在棋盘上，使得每行、每列有且只有一个，每条对角线（包括两条主对角线的所有平行线）上至多有一个棋子。

上面的布局可以用序列 \(2\ 4\ 6\ 1\ 3\ 5\) 来描述，第 \(i\) 个数字表示在第 \(i\) 行的相应位置有一个棋子，如下：

行号 \(1\ 2\ 3\ 4\ 5\ 6\)

列号 \(2\ 4\ 6\ 1\ 3\ 5\)

这只是棋子放置的一个解。请编一个程序找出所有棋子放置的解。
并把它们以上面的序列方法输出，解按字典顺序排列。
请输出前 \(3\) 个解。最后一行是解的总个数。

输入格式

一行一个正整数 \(n\)，表示棋盘是 \(n \times n\) 大小的。

输出格式

前三行为前三个解，每个解的两个数字之间用一个空格隔开。第四行只有一个数字，表示解的总数。

样例 #1

样例输入 #1

6

样例输出 #1

2 4 6 1 3 5
3 6 2 5 1 4
4 1 5 2 6 3
4

提示

【数据范围】
对于 \(100\%\) 的数据，\(6 \le n \le 13\)。

题目翻译来自NOCOW。

USACO Training Section 1.5

#include <iostream>
using namespace std;

const int N = 30;
bool r[N], d[N], ud[N];
int ans[N], res, n;

void dfs(int u)
{
    // cout << u << endl;
    if(u > n)
    {
        res++;
        //cout << res;
        if(res <= 3)
        {
            for(int i = 1; i <= n; ++ i)    cout << ans[i] << ' ';
            cout << endl;
        }
        return ;
    }
    for(int i = 1; i <= n; ++i)
    {
        if(!r[i] && !d[i + u] && !ud[n + i - u])
        {
            ans[u] = i;
            r[i] = true; d[i + u] = true; ud[n + i - u] = true;
            dfs(u + 1);
            ans[u] = 0;
            r[i] = false; d[i + u] = false; ud[n + i - u] = false;
        }
    }
}
int main()
{
    cin >> n;
    dfs(1);
    cout << res << endl;
    return 0;
}