旅行商（TSP）问题

题面

旅行商问题(TravelingSalesmanProblem，TSP)是一个经典的组合优化问题。经典的TSP可以描述为：一个商品推销员要去若干个城市推销商品，该推销员从一个城市出发，需要经过所有城市后，回到出发地。应如何选择行进路线，以使总的行程最短。

哈密顿环 改良圈

一个哈密顿环是一个包含所有顶点的圈，如果先求出一个哈密顿环，再不停地优化，构造新的更小的哈密顿环，就可以逼近问题的解。
设初始哈密顿环$C=v_1 v_2 v_3\cdots v_n v_1. $
(1)对于\(1\leq i< i+1< j\leq n\), 构造新的哈密顿环\(c_{ij}=v_1 v_2 \cdots v_i v_j v_{j-1} v_{j-2} \cdots v_{j+1} v_{j+2}\cdots v_n v_1\), 即删掉\(v_iv_{i+1}, v_jv_{j+1}\),添加\(v_{i}v_j, v_{i+1}v_{j+1}\). 如果\(W(v_iv_j)+w(v_{i+1}v_{j+1})<w(v_iv_{i+1})+w(v_jv_{j+1})\) 则以\(C_{ij}\)替换C,称其为的改良换。
(2) 重复（1）直到无法改进为止。
如果一次换三条边，效率更高，但是更多的话效率反而降低。

代码

以这样一道例题写代码

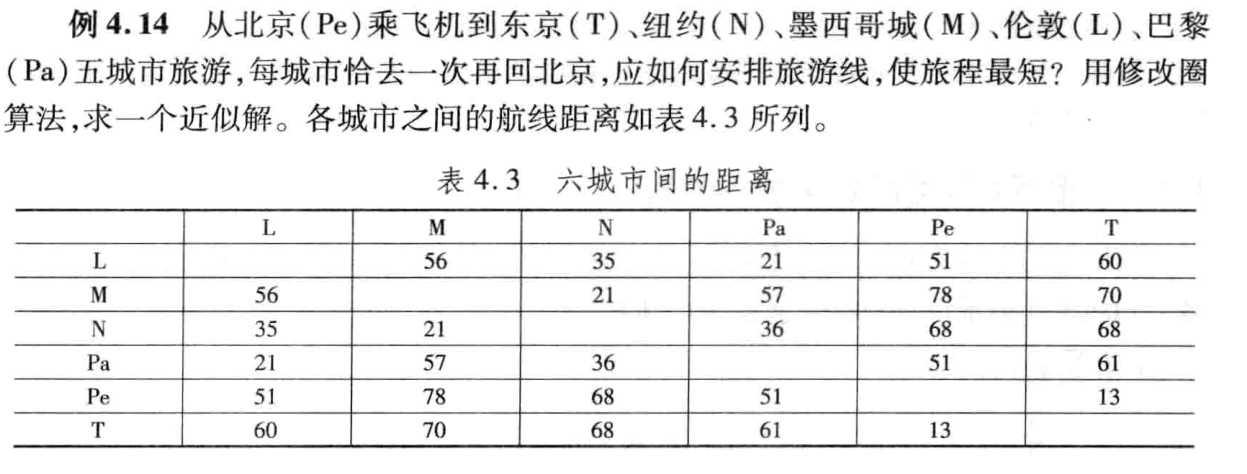
%初始化图
a=zores(6);
a(1,2) = 56; a(1,3) = 35; a(1,4) = 21; a(1,5) = 51; a(1,6) = 60; 
a(2,3) = 21; a(2,4) = 57; a(2,5) = 78; a(2,6) = 70; a(3,4) = 36; a(3,5) = 68; a(3,6) = 68; a(4,5) = 51; a(4,6) = 61;
a(5,6) = 13;
a = a + a';
%初始化完成
L = size(a,1);
c = [5 1:4 6 5];%选一个初始圈
[circle, long] = modifycircle(a,L,c)%定义函数modifycircle来修改边

function [circle, long] = modifycircle(a,L,c)
  for k = 1:L
    flag=0;%推出标志
    for m = 1:L-2 %算法中的i
      for n = m+2:L %算法中的j
        if a(c(m),c(n)) + a(c(m+1),c(n+1))<a(c(m),c(n+1)) + a(c(m+1),c(n))
          c(m+1:n) = c(n:-1:m+1); flag = flag+1;% 如果本来的边是从12，56，现在是15，26，即变为154326，是n:-1:m+1
        end
      end
    if flag == 0 %已经最优
      long = 0;%计算最优结果
      for i=1:L
        long = long + a(c(i),c(i+1))
      end
    circle = c;
    return;
    end
end

整数规划

用\(x_{ij}=0 or 1\) 表示是否走这条路。
\(d_{ij}\)表示两城市间的距离。

用matlab写有点繁琐，所以只是理论可行。

还可以用蒙特卡洛，神经网络等算法模拟或近似