最小费用最大流问题

什么是最小费用最大流

最小费用最大流问题，是指在图中找到一条费用最小的途径，同时它的流量最大。
用数学表示为，
\(x=(x_{ij})\)表示一个可行流
\(w=(w_{ij})\)表示单位通过改弧的费用
那么一个可行流的总费用为\(\sum_{(v_i,v_j)\in A}w_{ij}\cdot x_{ij}\)

最小费最大流问题相比单纯的最大流问题还有一个限制条件，总费用要最小，这就要求在调整流量的同时要让费用尽可能小。

线性规划语言描述

用数学规划的语言来解最小费用最大流为：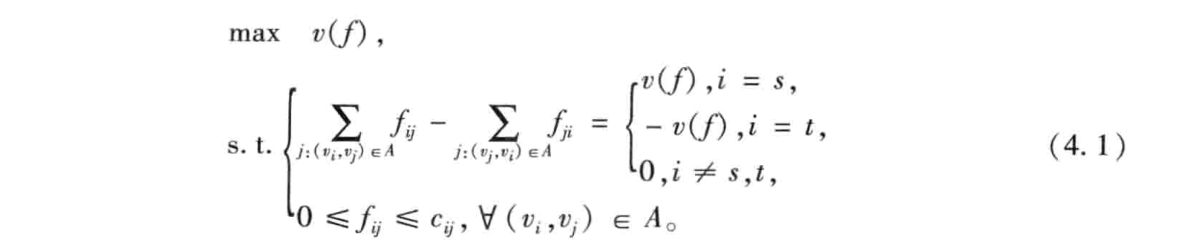

所以我们可以先求最大流，然后在发点、收点流量已知的情况下用线性规划求解最小费用。

matlab代码实现

以这张网络图为例

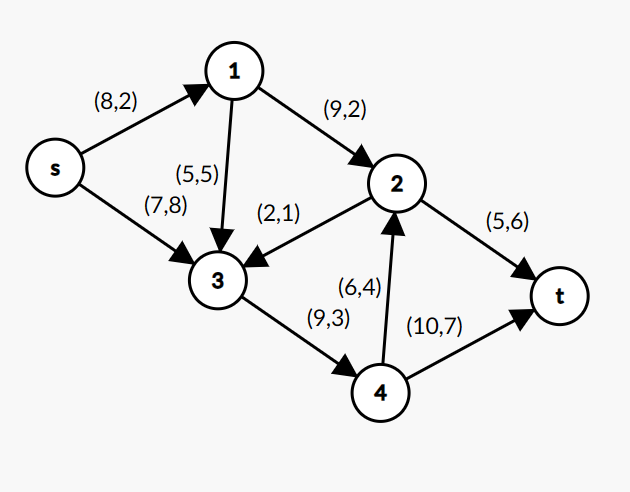
（u,v）分别表示网络的流量和费用。

%% 通过最大流算法求出最大流量% 定义网络容量矩阵
networkCapacity = [
    0, 9, 5, 0, 0, 0;
    0, 0, 2, 0, 0, 5;
    0, 0, 0, 9, 0, 0;
    0, 6, 0, 0, 0, 10;
    8, 0, 7, 0, 0, 0;
    0, 0, 0, 0, 0, 0
];

% 定义源点和汇点
sourceNode = 5;
sinkNode = 6;

% 调用最大流算法
[maxFlowValue, flowMatrix] = maxflow(networkCapacity, sourceNode, sinkNode);%求解结果为14，后面用得到.

%% 线性规划求最小费用
% 定义目标函数的系数向量
costCoefficients = [2; 8; 5; 2; 3; 1; 4; 6; 7];

% 定义等式约束的系数矩阵和常数向量，中间节点出入流量和为0
equalityConstraintsMatrix = [
    1, 1, 0, 0, 0, 0, 0, 0, 0;
    1, 0, -1, -1, 0, 0, 0, 0, 0;
    0, 1, 1, 0, -1, 1, 0, 0, 0;
    0, 0, 0, 1, 0, -1, 1, -1, 0;
    0, 0, 0, 0, 1, 0, -1, 0, -1;
    0, 0, 0, 0, 0, 0, 0, 1, 1
];
equalityConstraintsVector = [14; 0; 0; 0; 0; 14];%s，t点的初始流量最大

% 定义变量的下界和上界
variableLowerBounds = [0; 0; 0; 0; 0; 0; 0; 0; 0];
variableUpperBounds = [8; 7; 5; 9; 9; 2; 6; 5; 10];

% 调用 linprog 函数求解线性规划问题
[optimalSolution, optimalObjectiveValue, exitFlag, outputStructure] = ...
    linprog(costCoefficients, [], [], equalityConstraintsMatrix, ...
    equalityConstraintsVector, variableLowerBounds, variableUpperBounds);

% 显示结果
fprintf('Optimal solution:\n'); disp(optimalSolution);
fprintf('Optimal objective value:\n'); disp(optimalObjectiveValue);
fprintf('Exit flag:\n'); disp(exitFlag);
fprintf('Output structure:\n'); disp(outputStructure);