SFLS 初一第一学期12.5&12.6 难点重点知识点易错点整理

\(12.5\) 用数轴上的点表示实数

实数与数轴上的点之间的关系

首先，我们提出一个问题：怎么用数轴上的点表示所有实数？
对于这个问题，我们先将实数分为有理数部分和无理数部分。

有理数部分

我们知道，有理数可以用 \(\frac{p}{q}\) 表示，其中 \({\color{Red}p,q\in Z, q\ne 0, (p,q)=1}\)。那么有理数可以在数轴上很轻松的用等分法表示。（这里方法不做赘述）

无理数部分

无理数中最经典的就是根号类。这一类可以很轻松的在数轴上做出对应的点，如下图：

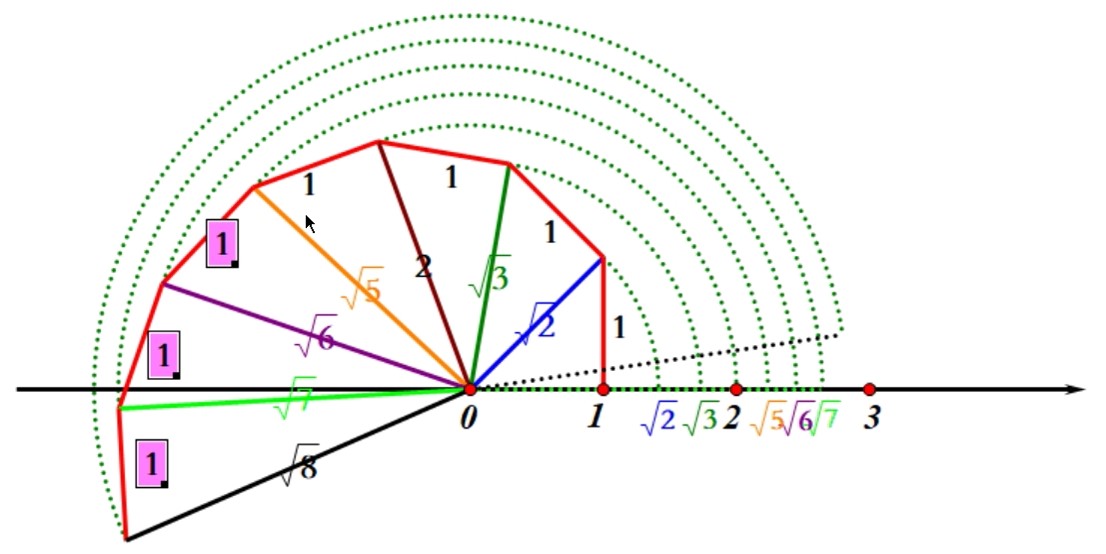
其它无理数虽然无法用几何法绘制，但也是可以表示的。

经过上面的论证，我们可以得出以下结论：
每一个实数都可以用数轴上的点来表示，而且这样的点是 \({\color{Red}唯一的}\) ，反过来，数轴上的一个点都可以用 \({\color{Red}唯一的}\) 一个实数表示。
我们也可以用简洁的话描述：
数轴上的点和实数成 \({\color{Red}一一对应}\)。

绝对值

这个比较简单，一个数的绝对值就是它在数轴上到原点的距离。不做赘述。

比大小

这是一个非常重要的考点，一共有 \(7\) 种方法，见下：

方法一：估读法

例如：

1. \(\pi <\frac{7}{22}<\sqrt{10}\)
2. \(\sqrt{7}-2<\frac{1}{\sqrt{7}-2}\)

方法二：比较根号下的数

例如：

1. $\sqrt{3}>\sqrt[3]{4} $
2. \(-3\sqrt{5}<-2\sqrt{11}\)

方法三：乘方法

例如：

1. \(4\sqrt{13}>3\sqrt{17}\)

方法四：赋值法

例如：

1. 若 \(0<x<1\)，则 \(\frac{1}{x}, \sqrt{x}, x, x^2\) 的大小关系为：\(\frac{1}{x}>\sqrt{x}>x>x^2\)

方法五：结论法

若 \(0<x<1\)，则 \(\frac{1}{x}, \sqrt{x}, x, x^2\) 的大小关系为：\(\frac{1}{x}>\sqrt{x}>x>x^2\)
若 \(x>1\)，则 \(\frac{1}{x}, \sqrt{x}, x, x^2\) 的大小关系为：\(\frac{1}{x}<\sqrt{x}<x<x^2\)

方法六：平方法

例如：

1. \(\sqrt{2}+\sqrt{5}<\sqrt{3}+\sqrt{4}\)
2. \(2+\sqrt{5}>\sqrt{3}+2\sqrt{2}\)

方法七：倒数法

例如：

1. \(\sqrt{2008}-\sqrt{2007}<\sqrt{2007}-\sqrt{2006}\)
2. \(2\sqrt{2}-\sqrt{13}>\sqrt{3}-2\sqrt{2}\)

两点间距离公式

这个也很简单，\(|a-b|\)。不做赘述。

\(12.6\) 实数的运算

加减法

实数加减法很简单，就是“合并同类项”。 \({\color{Red}注意变号}\) 即可，不做赘述。

乘除法

实数乘除法有两个主要的公式：

1. \(\sqrt{a}\times \sqrt{b}=\sqrt{ab}\)
2. \(\sqrt{\frac{a}{b}}=\frac{\sqrt{a}}{\sqrt{b}}\)

它们的成立条件都是 \(a\ge 0,b\ge 0\)，但是第二个公式的逆推条件为 \(a\ge 0, {\color{Red}b>0}\)。
公式就是这样，正常使用即可。注意，计算结果 \({\color{Red}要化简}\)；多观察，发现简便方法。

分母有理化

分母中单个根号

这种情况最简单，下面根号内配成完全平方数，上面相应的乘上那个数即可。
例如：

1. \(\frac{4}{\sqrt{12}}=\frac{2\sqrt{3}}{3}\)

分母中两个根号

可以使用平方差公式，例如：

1. \(\frac{1}{\sqrt{2}-\sqrt{3}}=-(\sqrt{2}+\sqrt{3})\)
2. \(\frac{1}{3\sqrt{2}+4\sqrt{3}}=\frac{4\sqrt{3}-3\sqrt{2}}{40}\)

也可以用因式分解法，例如：

1. \(\frac{a-5\sqrt{ab}+6b}{\sqrt{a}-2\sqrt{b}}=\sqrt{a}-3\sqrt{b}\)
2. \(\frac{x\sqrt{x}+y\sqrt{y}}{\sqrt{x}-\sqrt{y}}=x+\sqrt{xy}+y\)

分母中三个根号

也是使用凑平方差的方法，例如：

1. \(\frac{1}{1-\sqrt{2}+\sqrt{3}}=\frac{2-\sqrt{2}+\sqrt{6}}{4}\)

有的时候有简便运算，例如：

1. \(\frac{5+\sqrt{6}+\sqrt{10}+\sqrt{15}}{\sqrt{2}+\sqrt{3}+\sqrt{5}}=\frac{\sqrt{2}+\sqrt{3}+\sqrt{5}}{2}\)

其他情况

有的题目可以直接通分做，也比较简单，例如：

1. \(\frac{7\sqrt{11}-11\sqrt{7}}{7\sqrt{11}+11\sqrt{7}}-\frac{7\sqrt{11}+11\sqrt{7}}{7\sqrt{11}-11\sqrt{7}}=\sqrt{77}\)

有的题目可以裂项，例如：

1. \(\frac{1-2\sqrt{2}-\sqrt{3}}{(1-\sqrt{2})(\sqrt{2}+\sqrt{3})}=\sqrt{3}+1\)

有的题目取倒数之后做比较简单，例如：

1. \(\frac{(\sqrt{3}+\sqrt{5})(\sqrt{5}-\sqrt{7})}{\sqrt{3}+2\sqrt{5}-\sqrt{7}}=\frac{\sqrt{3}-\sqrt{7}}{2}\)

复合根式

方法一：配方

这是复合根式中最常用的一种方法了，将根号内的式子配方，再开方。注意， \({\color{Red}开出来的时候要有绝对值保护}\)！例如：

1. \(\sqrt{7+2\sqrt{12}}=|\sqrt{3}+\sqrt{4}|=\sqrt{3}+2\)

有的时候最大的根号里的根号系数不是 \(2\)，这时就需要将 \(2\) 凑出来，例如：

1. \(\sqrt{6-4\sqrt{2}}=\sqrt{6-2\sqrt{8}}=2-\sqrt{2}\)
2. \(\sqrt{6-\sqrt{20}}=\sqrt{6-2\sqrt{5}}=\sqrt{5}-1\)
3. \(\sqrt{3-\sqrt{5}}=\frac{\sqrt{6-2\sqrt{5}}}{\sqrt{2}}=\frac{\sqrt{10}-\sqrt{2}}{2}\)

有的时候有很多层根号，例如：

1. \(\sqrt{17-4\sqrt{9+4\sqrt{5}}}=\sqrt{17-8-4\sqrt{5}}=\sqrt{5}-2\)

有的时候会用到 \(3\) 项的完全平方公式，例如：

1. \(\sqrt{6+2\sqrt{2}+2\sqrt{3}+2\sqrt{6}}=1+\sqrt{2}+\sqrt{3}\)

方法二：平方法

有时，会有两个复合根式相加或者相减，这个时候可以使用平方法。但是注意：\({\color{Red}要先判断式子的正负}\)！例如：

1. \(\sqrt{5+\sqrt{21}}+\sqrt{5-\sqrt{21}}=\sqrt{(\sqrt{5+\sqrt{21}}+\sqrt{5-\sqrt{21}})^2}=\sqrt{10+2\sqrt{4}}=\sqrt{14}\)
2. \(\sqrt{5-\sqrt{21}}-\sqrt{5+\sqrt{21}}=-\sqrt{(\sqrt{5-\sqrt{21}}-\sqrt{5+\sqrt{21}})^2}==-\sqrt{10-2\sqrt{4}}=-\sqrt{6}\)

混合运算

最后，把上面的东西混合起来，就是混合运算啦~

近似

近似数与准确数

准确数是什么？准确数就是完全符合实际地表示一个量的多少的数。
那近似数又是什么？近似数就是与准确数 \({\color{Red}达到了一定近似程度}\) 的数。
然后我们举个例子：班级中有 \(9\) 位同学身高为 \(1.65m\)。
其中，\(9\) 是准确数，而 \(1.65m\) 是近似数。

近似程度与精确度

那么，\(3.14\) 和 \(3.1415926535 8979323846 2643383279 5028841971 6939937510 5820974944 5923078164 0628620899 8628034825 3421170679 8214808651 3282306647 0938446095 5058223172 5359408128 4811174502 8410270193 8521105559 6446229489 5493038196 4428810975 6659334461 2847564823 3786783165 2712019091 4564856692 3460348610 4543266482 1339360726 0249141273 7245870066 0631558817 4881520920 9628292540 9171536436 7892590360 0113305305 4882046652 1384146951 9415116094 3305727036 5759591953 0921861173 8193261179 3105118548 0744623799 6274956735 1885752724 8912279381 8301194912 9833673362 4406566430 8602139494 6395224737 1907021798\) 都是 \(\pi\) 的近似数，它们有什么区别？
它们一个精确到了小数点后 \(2\) 位，一个精确到了小数点后 \(100\) 位。
这就是它们的近似程度不同。近似程度是什么？近似程度就是近似数与准确数的接近程度。
而对于近似程度的要求，就是精确度。
多于精确度的要求有三种描述方式：

• 保留 \(n\) 位小数或者精确到小数点后 \(n\) 位
• 精确到\(××\)位
• 保留 \(n\) 给有效数字（有效数字：除去前导零后的第一个数及其以后的数）

有的题目让你写出近似数，例如：

1. \(0.70589\) 精确到千分位：\(0.796\)
2. \(1.5972\) 精确到 \(0.01\)：\(1.60\)
3. \(80320\) 保留两个有效数字：\(8.0\times10^4\)
4. \(289.96\) 保留一位小数：\(290.0\)
5. \(23487834\) 精确到十万位：\(23500000\)

还有的题目让你写出近似数精确到了哪一位，有几个有效数字，例如：

1. \(2000\) 精确到了个位，有 \(4\) 个有效数字
2. \(0.0618\) 精确到了万分位，有 \(3\) 个有效数字
3. \(7.20万\) 精确到了百位，有 \(3\) 个有效数字
4. \(5.10\times10^5\) 精确到了千位，有 \(3\) 个有效数字

${\color{Purple} 好了，难点重点知识点易错点就这么些了。}\mathfrak{Bye}\sim $