Tarjan学习笔记

众所周知，Tarjan 可以用来求有向图的强连通分量，我们就不扯那些 dfs 生成树，前向边、返祖边之类的东西，直接步入正题。

准备工作

Tarjan 算法本质上是一次 dfs 的过程，我们用 $dfn[u]$ 记录 $u$ 结点被 dfs 到的顺序，用 $low[u]$ 记录 $u$ 能到达的所有结点中最小的 $dfn$（包括自己）（详细定义：能够回溯到的最早的已经在栈中的结点。设以 $u$ 为根的子树为 $subtre{e}_u$，则 $low[u]$ 定义为以下结点的 $dfn$ 的最小值：$subtre{e}_u$ 中的结点；从 $subtre{e}_u$ 通过一条不在搜索树上的边能到达的结点。）。$dfn$ 很好维护，dfs 的过程中记录一下即可。接下来为重头戏：$low[u]$ 的维护与强联通分量的计算。

正式开始

考虑从一个结点 $u$ 到另一个结点 $v$ 的过程中会发生什么。

1. 如果 $v$ 在栈中（即那个节点还没计算完），那么 $v$ 一定是 $u$ 的祖先，则用 $\mathbf{dfn}[v]$ 更新 $low[u]$。
2. 如果 $v$ 访问过且不在栈中（即计算完了），那么装作无事发生。
3. 如果 $v$ 还没被访问过，那么递归访问，用 $\mathbf{low}[v]$ 更新 $low[u]$。

将 $u$ 能直接到达的所有 $v$ 都算完后，就可以计算强连通分量了。我们发现，如果一个结点算完后 $low[u]=dfn[u]$，则说明：这个结点是当前强联通分量中最先到达的（即 $dfn$ 最小的，称为这个强连通分量的根）

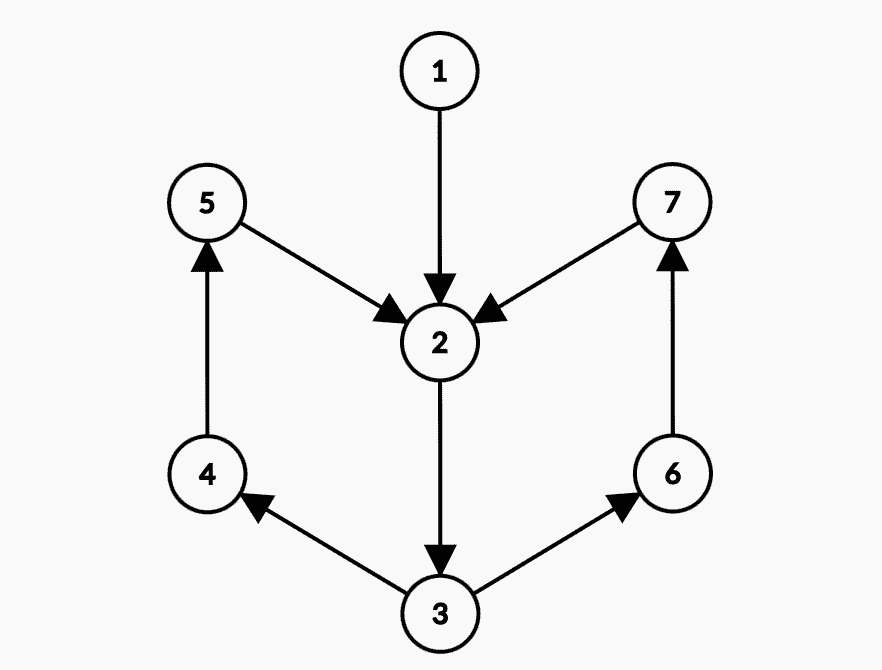
在这个图中，$2$ 号节点就是强连通分量 $\{2,3,4,5,6,7\}$ 中的根。

这时候，我们就可以处理 $u$ 的强连通分量了！循环让结点出栈，直到栈顶元素为 $u$ 自己（因为 $u$ 是强连通分量的根，所以它一定是该强连通分量在栈中最靠前的），这些节点都在同一个以 $u$ 为根的强连通分量里。

如果一个结点算完后 $low[u]\ne dfn[u]$，则意味着它能到达一个它的祖先，我们暂时先不处理它，也不出栈（还没算完强连通分量怎么能出栈呢），直接返回，到他的那个强连通分量的根的时候再去算强连通分量。

代码实现

//num记录当前一共遍历了几个结点，用于计算新结点的dfn
//col[i]记录第节点i在哪个强连通分量里，root[i]表示i所在强连通分量的根
//colnum记录当前一共算完了几个强连通分量，用来计算新强连通分量的编号
int tarjan(int now) {
	s.push(now),vis[now]=1;
	low[now]=dfn[now]=++num;
	for(int i=head[now];i;i=e[i].next)
		if(!dfn[e[i].to])
			low[now]=min(low[now],tarjan(e[i].to));
		else if(vis[e[i].to])
			low[now]=min(low[now],dfn[e[i].to]);
	if(dfn[now]==low[now]) {
		vis[now]=0;
		col[now]=++colnum,root[now]=now;
		while(s.top()!=now) {
			col[s.top()]=colnum,root[s.top()]=now;
			vis[s.top()]=0,s.pop();
		}
		s.pop();
	}
	return low[now];
}

扩展阅读

建议参考阅读这篇文章的手动模拟算法的部分，会有更直观的理解。

有兴趣看看更严谨的说明，请上 oi-wiki 观看。