ABC-267解题报告

比赛传送门

D. Index × A(Not Continuous ver.)

题目传送门

令 \(f[i][j]\) 表示考虑序列的前 \(i\) 位，\(i\) 为取的 \(j\) 个元素时的最大贡献，则 \(f[i][j]=\max\limits_{1\le k<i} f[k][j-1]\)。用 \(g[j]\) 维护取 \(j\) 个元素时的最大贡献，即可将转移优化为 \(O(1)\)，总复杂度 \(O(n^2)\)。

E. Erasing Vertices 2

题目传送门

可以想到一个很显然的贪心策略：每次取邻居的权值和最小的节点删除。

具体实现上可以采用类似堆优化 \(Dijkstra\) 的思想，用优先队列维护节点和邻居权值，每次取堆顶元素，松弛邻居节点。

F. Exactly K Steps

题目传送门

首先可以想到和树的直径有关。

做法 1（赛时做法）

对于在直径上的点，距离为 \(K\) 的点要么不存在，要么在直径上。这个比较容易处理。

对于不在直径上的点，可以“向直径跑 \(K\) 步”。可以对于每个直径上的点，都往直径“旁边”跑一遍 DFS 来统计答案。由于不能每个点都跑一遍 DFS，可以将询问离线下来，搜到哪个点就记录答案。

做法 2

设直径的两端分别为 \(L,R\)，则无论是不是直径上的点，距离为 \(K\) 的点要么不存在、要么可以往 \(L\) 跑 \(K\) 步、要么可以往 \(R\) 跑 \(K\) 步。于是从 \(L\) 和 \(R\) 分别跑一遍 DFS 即可。（当然也要离线询问）

G. Increasing K Times

题目传送门

一个排列计数题，可以考虑从小往大插入数。

状态：设 \(f[i][j]\) 表示插入了前 \(i\) 小的数，增长 \(j\) 次的方案数。可以维护一个 \(cnt\) 表示已经插入了多少个“与当前插入的数相同的数”，转移会用到。

转移：新插入的数一定是所有数中最大的，从这点入手转移。先考虑什么时候增长的次数不变？放在一个本来就增长的两个数中间。这种情况的方案为 \(j\) 种

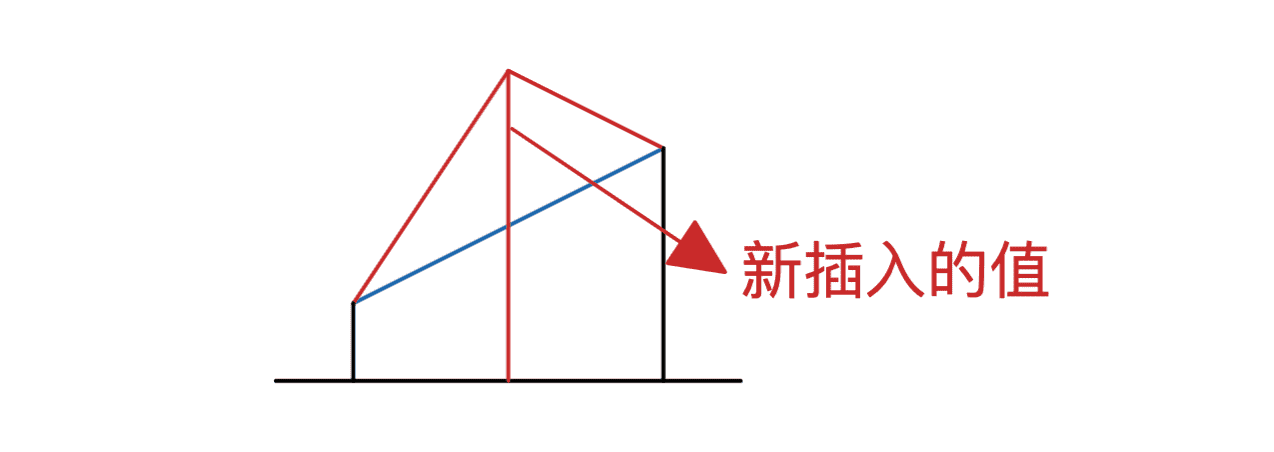
只有这一种情况吗？当然不是。还可以放在“与它相同的数”的后面。这种情况有 \(cnt\) 种。这两种情况并不会重复计算，因为当前数一定是最大的，所以“与它相同的数”后面的位置原先一定不会上升。还有一种容易忽略的情况时放在整个序列的开头，它不属于以上任何一种情况而满足条件。

综上，\(f[i][j]\leftarrow f[i-1][j]\times(j+cnt+1)\)

什么时候增长的次数会改变？自然是除了以上的情况都会改变。而显然改变只能多 1 次增长，所以 \(f[i][j]\leftarrow f[i-1][j-1]\times(i-j-cnt-1)\)

所以转移方程为：

\[f[i][j]=f[i-1][j]\times(j+cnt+1)+f[i-1][j-1]\times(i-j-cnt-1) \]