图的思维导图及总结

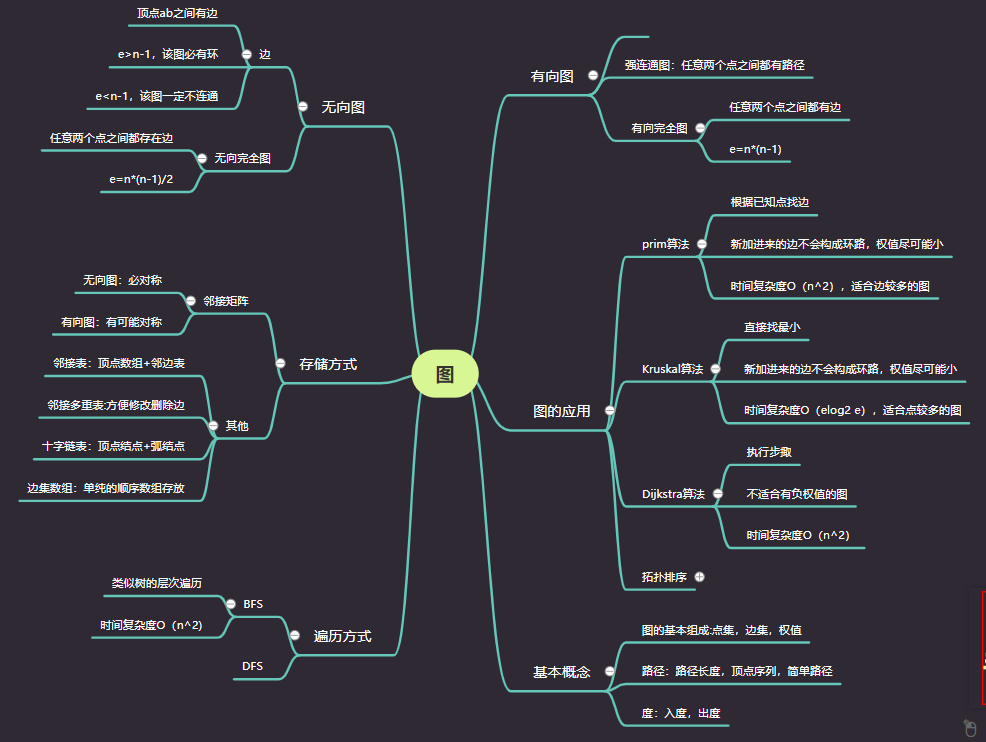
重要概念笔记

1.有向图
若E是有向边（简称弧）的有限集合时，则G为有向图。弧是顶点的有序对，记为<v,w>，其中 v，w 是顶点，v 是弧尾，w 是弧头。称为从顶点v到顶点w的弧。
2.无向图
若E是无向边（简称边）的有限集合时，则G为无向图。边是顶点的无序对，记为 (v,w) 或(w,v) ，且有 (v,w) =(w,v) 。其中 v，w 是顶点。
3.完全图
无向图中任意两点之间都存在边，称为无向完全图。
有向图中任意两点之间都存在方向向反的两条弧，称为有向完全图.
4.连通、连通图、连通分量
在无向图中，两顶点有路径存在，就称为连通的。若图中任意两顶点都连通，同此图为连通图。无向图中的极大连通子图称为连通分量。
5.强连通图、强连通分量
在有向图中，两顶点两个方向都有路径，两顶点称为强连通。若任一顶点都是强连通的，称为强连通。有向图中极大强连通子图为有向图的强连通分量。
6.图的两种存储结构

1. 邻接矩阵，原理就是用两个数组，一个数组保存顶点集，一个数组保存边集。
2. 邻接表，邻接表是图的一种链式存储结构。这种存储结构类似于树的孩子链表。对于图G中每个顶点Vi，把所有邻接于Vi的顶点Vj链成一个单链表，这个单链表称为顶点Vi的邻接表。
3. 深度优先搜索遍历
   深度优先搜索DFS遍历类似于树的前序遍历。其基本思路是：
   a) 假设初始状态是图中所有顶点都未曾访问过，则可从图G中任意一顶点v为初始出发点，首先访问出发点v，并将其标记为已访问过。
   b) 然后依次从v出发搜索v的每个邻接点w，若w未曾访问过，则以w作为新的出发点出发，继续进行深度优先遍历，直到图中所有和v有路径相通的顶点都被访问到。
   c) 若此时图中仍有顶点未被访问，则另选一个未曾访问的顶点作为起点，重复上述步骤，直到图中所有顶点都被访问到为止。
4. 广度优先搜索遍历
   广度优先搜索遍历BFS类似于树的按层次遍历。其基本思路是：
   a) 首先访问出发点Vi
   b) 接着依次访问Vi的所有未被访问过的邻接点Vi1，Vi2，Vi3，…，Vit并均标记为已访问过。
   c) 然后再按照Vi1，Vi2，… ，Vit的次序，访问每一个顶点的所有未曾访问过的顶点并均标记为已访问过，依此类推，直到图中所有和初始出发点Vi有路径相通的顶点都被访问过为止。

疑难问题

1.用prim算法求最小生成树时，边上的权怎么不能为负呢？
权值一般代表一个抽象出来的路径长度
2.不会辨别深度优先生成树和广度优先生成树