数学建模学习笔记 | 线性代数模型
矩阵的分类
1、矩阵(二维数组)
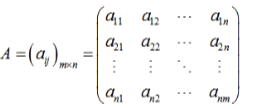
2、其他矩阵(列矩阵、行矩阵,方阵)
- 列矩阵(列向量)
- 行矩阵(行向量)
- 方阵(行与列一样)
3、单位矩阵

矩阵的线性运算
- 加法(两个规模一样的矩阵,元素相加)
- 数乘:
- 乘法:
- 定义:
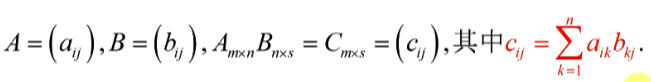
-
内积:
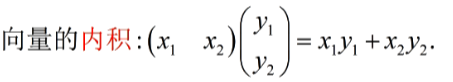
- 例:
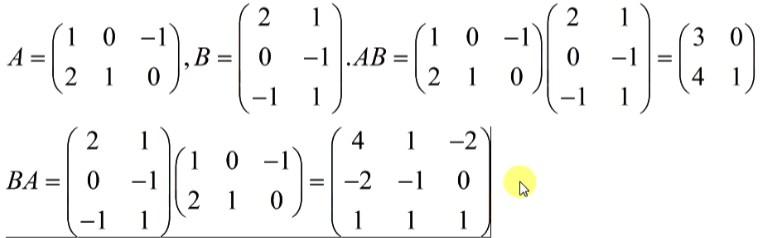
- 运算过程(参考向量的内积的运算):
- AB👉1*2+0*0+-(1)*(-1)=3;2*2+1*0+0*(-1)=4;1*1+0*(-1)+(-1)*1=0;2*1+1*(-1)+0*1=1
-
矩阵乘法定义时要求左边矩阵的列数和右边矩阵的行数相等
-
矩阵的乘法运算,不满足交换律
-
矩阵的乘法运算与线性运算,满足分配律 ,即:
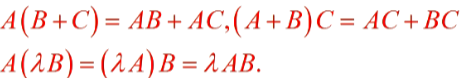
- 定义:
-
- 线性变换:
- 含义:若A是一个线性变换,则A可以把任意向量关于横轴对称
- 推算过程:
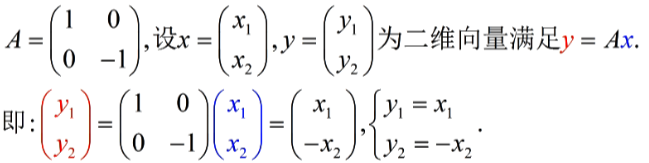
- 线性变换:
特征值与特征向量
- 定义:给定方阵A,如果存在向量x和常数λ使得Ax = λx,则称
- λ:A的特征值
- x:A的特征向量
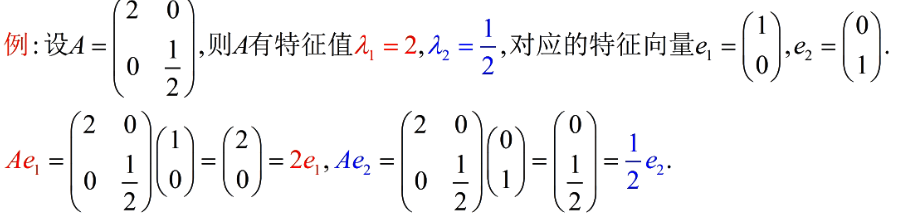
-
事实上,如果e1是特征值λ1的特征向量,其任意的非零数乘ke1也是特征值λ1的特征向量
- 参考:https://www.cnblogs.com/zzdbullet/category/1356164.html
https://chenxuefan.cn


 浙公网安备 33010602011771号
浙公网安备 33010602011771号