11_数据降维PCA

1.sklearn降维API：sklearn. decomposition

2.PCA是什么：主成分分析

　　本质：PCA是一种分析、简化数据集的技术。

　　目的：是数据维数压缩，尽可能降低原数据的维数（复杂度），损失少量信息。

　　作用：可以削减回归分析或者聚类分析中特征的数量。

　　当特征达到上百的时候，考虑是否要使用PCA来删除部分特征。

3.高维度数据容易出现的问题：特征之间通常是线性相关的。

4.PCA语法：

　　PCA(n_components=None) 将数据分解为较低维数空间

　　　　n_components:可以是小数，也可以是整数。为小数时，指定保存多少的数据量，通常是0.9~0.95,表示保存90%到95%的数据量。

　　　　　　　　　　　为整数时，表示减少到多少特征数量，一般不使用整数。

　　PCA.fit_transform(X) X:numpy array格式的数据[n_samples,n_features] 返回值：转换后指定维度的array

5.PCA演示过程：

　　1.初始化PCA,指定减少后的维度。

　　2.调用fit_transform

 

案例：

def pca():
    """
    主成分分析进行特征降维
    :return:
    """
    pca = PCA(n_components=0.9)
    data = pca.fit_transform([[2, 8, 4, 5], [6, 3, 0, 8], [5, 4, 9, 1]])
    print(data)


if __name__ == '__main__':
    # normalization()
    # stand()
    # im()
    # var()
    pca()

结果：

[[ 1.28620952e-15  3.82970843e+00]
 [ 5.74456265e+00 -1.91485422e+00]
 [-5.74456265e+00 -1.91485422e+00]]

 

6.简单的降维过程：

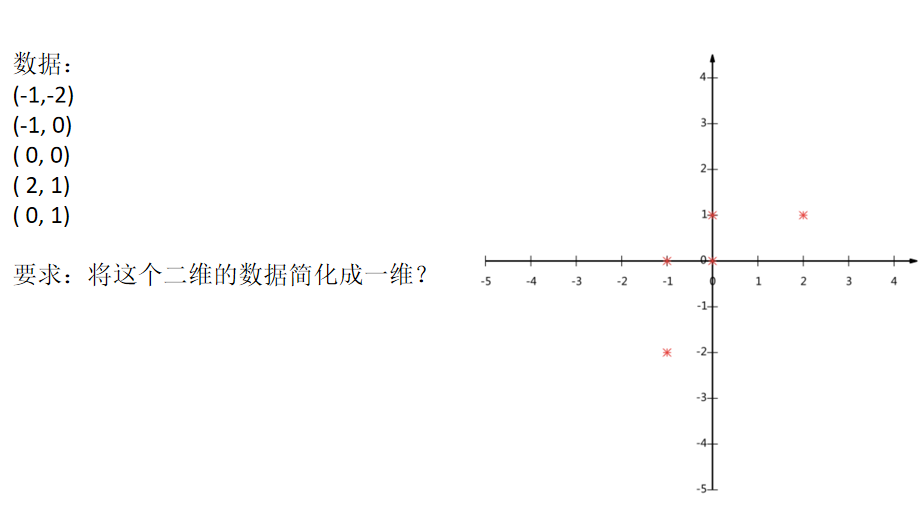
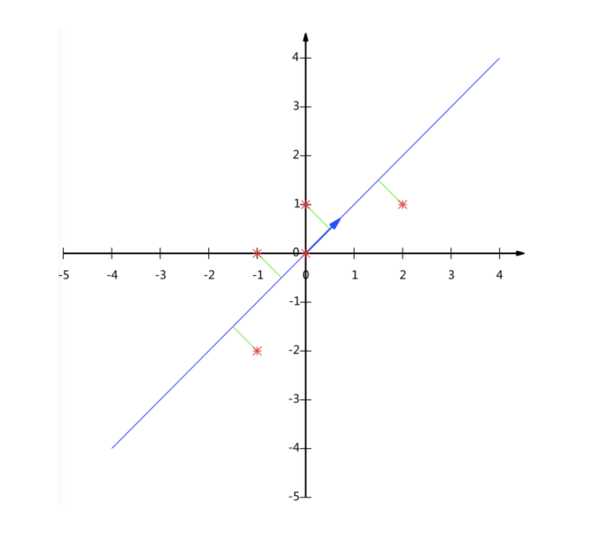
可以投向x轴和y轴，但是会丢失数据点，五个点变成三个点。