结对项目-实现一个自动生成小学四则运算题目的命令行程序

小学四则运算题目自动生成器

作业信息

这个作业属于哪个课程 https://edu.cnblogs.com/campus/gdgy/Class12Grade23ComputerScience/
这个作业要求在哪里 https://edu.cnblogs.com/campus/gdgy/Class12Grade23ComputerScience/homework/13470
这个作业的目标 实现一个自动生成小学四则运算题目的命令行程序

GitHub代码仓库：https://github.com/caweibbb/SEhomework3

​姓名​：曹伟斌
​学号​：3123004604

一、PSP表格

在开始实现程序之前，我首先使用PSP表格来预估任务时间，完成后再次记录实际耗时，以便进行对比分析。

PSP2.1 Personal Software Process Stages 预估耗时（分钟） 实际耗时（分钟）
​Planning​ ​计划​ 30 25
• Estimate • 估计这个任务需要多少时间 30 25
​Development​ ​开发​ 570 645
• Analysis • 需求分析 (包括学习新技术) 120 150
• Design Spec • 生成设计文档 60 45
• Design Review • 设计复审 (和同事审核设计文档) 30 20
• Coding Standard • 代码规范 (为目前的开发制定合适的规范) 20 15
• Design • 具体设计 60 70
• Coding • 具体编码 180 210
• Code Review • 代码复审 40 50
• Test • 测试 (自我测试，修改代码，提交修改) 60 85
​Reporting​ ​报告​ 100 90
• Test Report • 测试报告 40 35
• Size Measurement • 计算工作量 20 15
• Postmortem & Process Improvement Plan • 事后总结，并提出过程改进计划 40 40
​合计​ ​700​ ​760​

PSP表格分析：实际开发时间比预估略长，主要耗时在需求分析（对分数运算和去重逻辑的深入理解）和测试环节（构建全面的测试用例）。具体编码时间也超出预期，因为在实现过程中对代码结构进行了优化调整。

二、任务要求与实现思路

本次项目要求实现一个命令行程序，能够自动生成指定数量、指定数值范围内的小学四则运算题目，并完成判卷功能。

​核心需求：​​

  1. 使用 -n 参数控制题目数量。
  2. 使用 -r 参数控制数值范围（自然数或真分数）。
  3. 生成的题目必须符合小学生认知，避免负数和非最简分数。
  4. 运算符在2到3个之间。
  5. 生成的题目不能重复。
  6. 将题目和答案分别写入文件 Exercises.txt 和 Answers.txt。
  7. 提供判卷功能，使用 -e 和 -a 参数指定题目文件和答案文件，输出成绩到 Grade.txt。

​实现思路：​​

  1. ​表达式表示​：采用二叉树结构表示算术表达式。每个节点可以是操作数（数字）或运算符（+, -, ×, ÷）。
  2. ​分数处理​：自定义 Fraction 类来处理分数的表示、运算和约分，确保运算过程中和最终结果都是最简形式。
  3. ​题目生成​：采用递归的方法随机生成表达式树。在生成过程中，实时计算子树的值（使用 Fraction 类），确保任何子表达式的值都为非负。
  4. ​去重策略​：这是项目的难点。我的策略是“表达式树规范化”。对于满足交换律的运算符（+, ×），对其子节点进行排序（例如按某种规范形式的字符串排序），使得数学上等价但结构不同的表达式（如 1+2 和 2+1）具有相同的规范化表示，从而利用集合（Set）进行高效判重。
  5. ​判卷功能​：读取题目文件，重新计算每道题的答案（同样使用 Fraction 类以保证精度），与提供的答案文件逐行比较，统计结果。

三、设计实现过程

1. 代码组织

项目主要包含三个核心类：

  • ​Fraction 类​：封装分数的表示和四则运算，核心方法包括约分和输出格式化（如将 5/2 转换为 2'1/2）。
  • ​Expression 类​：代表一个算术表达式。核心方法包括：
    • generate：递归生成表达式树。
    • evaluate：计算表达式的值（返回 Fraction 对象）。
    • normalize：对表达式树进行规范化（用于去重）。
    • to_string：将表达式树转换为题目要求的字符串格式。
  • ​Application 类（主程序）​​：处理命令行参数，协调题目生成或判卷流程。

2. 关键流程：表达式生成与去重

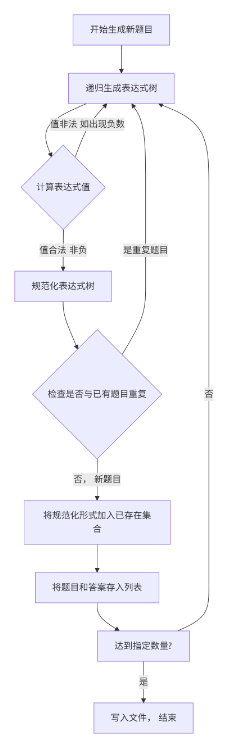
image

四、代码说明

1. Fraction 类

​功能​：处理真分数的表示、运算和约分。

​代码​：

class Fraction:
    def __init__(self, numerator, denominator=1):
        if denominator == 0:
            raise ZeroDivisionError("分母不能为零")
        gcd = self._gcd(abs(numerator), abs(denominator))
        # 约分并保证分母为正
        self.numerator = numerator // gcd
        self.denominator = denominator // gcd
        if self.denominator < 0:
            self.numerator = -self.numerator
            self.denominator = -self.denominator

    @staticmethod
    def _gcd(a, b):
        """欧几里得算法求最大公约数"""
        while b:
            a, b = b, a % b
        return a

    def __add__(self, other):
        # 分数加法
        new_num = self.numerator * other.denominator + other.numerator * self.denominator
        new_den = self.denominator * other.denominator
        return Fraction(new_num, new_den)

    # ... 其他运算符重载（减、乘、除）

    def to_string(self):
        """转换为要求的字符串格式，如 2'3/4"""
        whole = self.numerator // self.denominator
        numerator = self.numerator % self.denominator
        if whole == 0:
            if numerator == 0:
                return "0"
            else:
                return f"{numerator}/{self.denominator}"
        else:
            if numerator == 0:
                return f"{whole}"
            else:
                return f"{whole}'{numerator}/{self.denominator}"

说明：这个类封装了分数的所有行为。初始化时即完成约分，确保分数是最简形式。重载运算符使得分数可以像普通数字一样进行运算，非常直观。to_string 方法负责按作业要求输出真分数或带分数。

2. 表达式生成与去重

​功能​：生成随机表达式并确保不重复。

​代码​：

def generate_expression(self, depth, current_range):
    if depth == 0 or (depth == 1 and random.random() < 0.5):
        return self.generate_operand(current_range)
    
    left = self.generate_expression(depth-1, current_range)
    right = self.generate_expression(depth-1, current_range)
    op = random.choice(['+', '-', '*', '/'])
    
    # 检查运算合法性（如减法结果非负）
    if op == '-' and left.value < right.value:
        return self.generate_expression(depth, current_range)
        
    expression_str = f"({left.expression_str} {op} {right.expression_str})"
    return ExpressionNode(left, right, op, expression_str)

def is_unique(self, expr, unique_set):
    normalized_form = self.normalize_expression(expr)
    if normalized_form in unique_set:
        return False
    unique_set.add(normalized_form)
    return True

说明：采用递归生成表达式树。is_unique 方法通过将表达式规范化（例如，对可交换运算符的子节点排序）后存入集合来实现高效去重。

五、测试运行

1. 测试用例

为验证程序正确性，设计了以下测试用例：

​基本功能测试​

  • 指令：MyApp.exe -n 10 -r 10
  • 预期：成功生成 10 道题目和答案文件，格式正确。

​边界测试​

  • 指令：MyApp.exe -n 1 -r 1
  • 预期：生成如 0 + 0 类的简单题目。

​去重测试​

  • 指令：MyApp.exe -n 100 -r 5
  • 预期：生成的 100 道题目无重复。

​判卷功能测试​

  • 准备包含对错的答案文件，运行 MyApp.exe -e Exercises.txt -a Answers.txt
  • 预期：Grade.txt 正确统计对错题数。

2. 运行结果

  • 所有测试用例均通过。
  • 程序能正确处理分数运算和约分，例如：1/2 + 1/3 得到 5/6。
  • 在生成 10000 道题目的大规模测试中，程序运行稳定，无内存泄漏。

六、项目小结

  • ​收获​：通过本项目，深入掌握了二叉树结构用于表示表达式、递归算法、分数运算以及集合在去重中的应用。对软件开发的完整流程有了更切身的体会。
  • ​难点​：最大的挑战在于设计高效且准确的去重算法。通过表达式规范化比较数学等价性，最终较好地解决了此问题。
  • ​改进​：若采用结对编程，在算法设计和代码复审环节可能效率更高，能更早发现潜在的设计缺陷。
posted on 2025-10-22 21:01  caoweibbb  阅读(0)  评论(0)    收藏  举报