【算法设计与分析基础】21、动态规划-背包问题

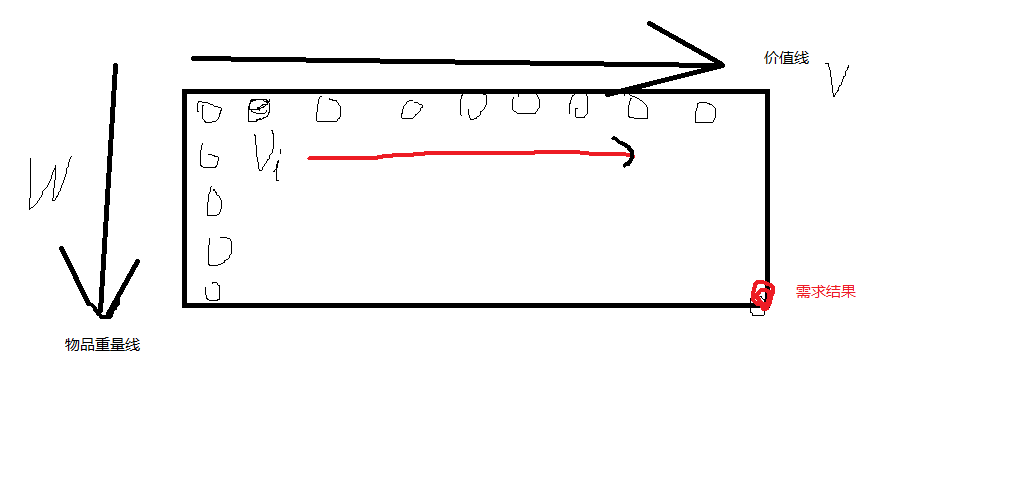
问题：

* 对一组物品：
* 重量为:w1,w2,w3....wn
* 价值为:v1,v2,v3,....vn
* 和一个可以存放重量为W的背包
* 求这些物品装进去如何才会是最右价值的装法

 

 

解题思路：

对于这些物品进行分类，判断第i个物品是否需要加入背包

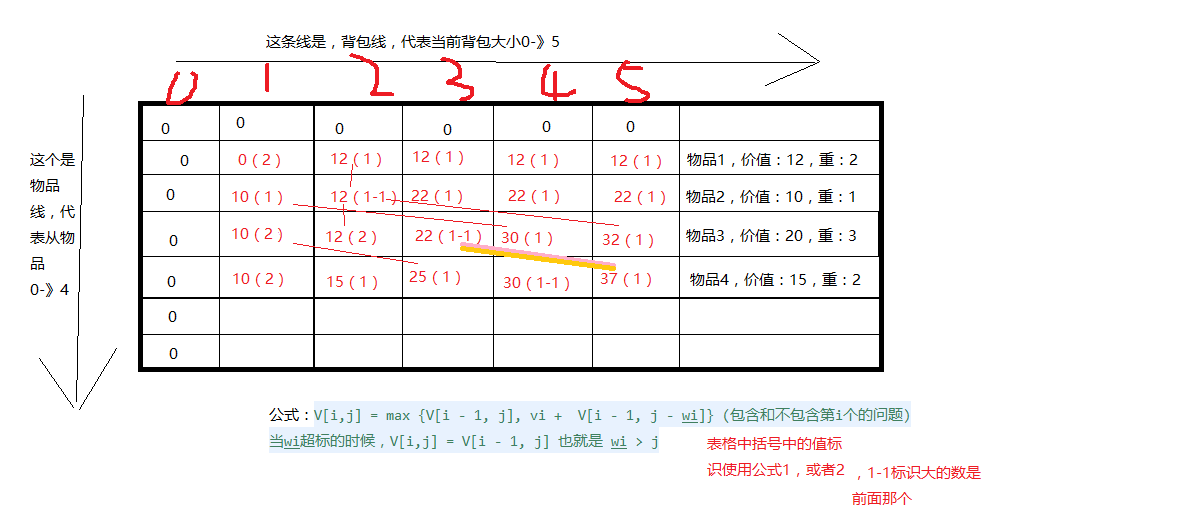
获取到的结果就是，放入前i个物品进入重量是j的方式是
V[i,j] = max {V[i - 1, j], vi + V[i - 1, j - wi]} (包含和不包含第i个的问题)
当wi超标的时候，V[i,j] = V[i - 1, j] 也就是 wi > j

 

 

 

 

问题求解：

 

 

 

解题：

package cn.xf.algorithm.ch08DynamicProgramming;

import org.junit.Test;

/**
 * 动态规划，背包问题
 * 
 * 对一组物品：
 * 重量为:w1,w2,w3....wn
 * 价值为:v1,v2,v3,....vn
 * 和一个可以存放重量为W的背包
 * 求这些物品装进去如何才会是最右价值的装法
 * .
 * 
 * @版权：福富软件 版权所有 (c) 2017
 * @author xiaof
 * @version Revision 1.0.0
 * @see:
 * @创建日期：2017年8月7日
 * @功能说明：
 *
 */
public class BackPack {
//    解题思路：对于这些物品进行分类，判断第i个物品是否需要加入背包
//    获取到的结果就是，放入前i个物品进入重量是j的方式是
//    V[i,j] = max {V[i - 1, j], vi +  V[i - 1, j - wi]} (包含和不包含第i个的问题)
//    当wi超标的时候，V[i,j] = V[i - 1, j] 也就是 wi > j
    /**
     * 
     * @param values  依次物品的价值
     * @param weight  依次物品的重量
     * @param W 背包大小
     */
    public int[][] typeBack(int values[], int weight[], int W) {
        int resultValue[][] = new int[values.length][W + 1];
        //初始化，当价值为0的时候，那么背包里面肯定没有物品
        for(int i = 0; i < W + 1; ++i) {
            resultValue[0][i] = 0;
        }
        //遍历所有的物品，并且遍历背包重量
        for(int i = 1; i < values.length; ++i) {
            //遍历所有物品，当背包大小为0的时候，那么价值结果肯定为0
            resultValue[i][0] = 0;
            for(int j = 1; j <= W; ++j) {
                //背包大小慢慢增加
                //当前物品i是否对应不同的背包是否放入的问题，价值是几何
                if(j > W || j - weight[i] < 0) {
                    //当前物品重量大于背包，背包不可能包含这个物品
                    resultValue[i][j] = resultValue[i - 1][j];
                } else {
                    resultValue[i][j] = maxValue(resultValue[i - 1][j], values[i] + resultValue[i - 1][j - weight[i]]);
                }
            }
        }
        
        return resultValue;
    }
    
    public int maxValue(int a, int b) {
        if(a > b) {
            return a;
        } else {
            return b;
        }
    }
    
    //对背包问题实现动态规划的记忆功能，避免对部门数据的重复计算
    public int MFKTypeBack(int result[][], int values[], int weight[], int i, int j) {
        //递归就是，判断需要求的位置的值是否已经存在，如果还没求出来，那么就递归
        int value;
        if(i == 0 || j == 0) {
            //递归终止条件
            value =  result[i][j];
        } else {
            if(result[i][j] <= 0) {
                //如果这个值还没有被获取出来
                //判断当前物品的重量是否超标
                if(j - weight[i] < 0) { //这个表示，如果背包中包含这个物品，去掉这个物品之后，背包中物品最少要不小于0
                    //当前物品重量大于背包，背包不可能包含这个物品
                    value = MFKTypeBack(result, values, weight, i - 1, j);
                } else {
                    value = maxValue(MFKTypeBack(result, values, weight, i - 1, j), 
                        values[i] + MFKTypeBack(result, values, weight, i - 1, j - weight[i]));
                }
                result[i][j] = value;
            }
        }
        return result[i][j];
    }
    
    
    @Test
    public void test1() {
        int weight[] = {0,2, 1, 3, 2};
        int values[]= {0, 12, 10, 20, 15 }; // 价值数组
        int W = 5;
        BackPack bp = new BackPack();
        int result[][] = bp.typeBack(values, weight, W);
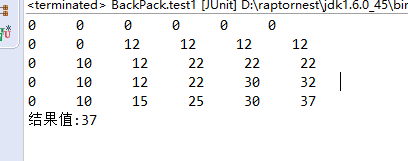
        for (int i = 0; i < result.length; i++) {
            for (int j = 0; j < result[0].length; j++) {
                System.out.print(result[i][j] + "     ");
            }
            System.out.println();
        }
        int result2[][] = new int[weight.length][W + 1];
        for(int i = 0; i < weight.length; ++i) {
            for(int j = 0; j < W + 1; ++j) {
                result2[i][j] = 0;
            }
        }
        //从第一个物品选中开始
        int valueR = bp.MFKTypeBack(result2, values, weight, 4, 5);
        System.out.println("结果值:" + valueR);
    }
    
}

　　

 

结果：