mex

 

# Description
有一个长度为n的数组{a1,a2,...,an}。

m次询问，每次询问一个区间内最小没有出现过的自然数

# Format

## Input
第一行n,m。

第二行为n个数。

从第三行开始，每行一个询问l,r

1<=n,m<=200000

0<=ai<=109

1<=l<=r<=n

## Output
一行一个数，表示每个询问的答案

# Samples

```input1
5 5
2 1 0 2 1
3 3
2 3
2 4
1 2
3 5
```

```output1
1
2
3
0
3
```

 

题解:主席树维护,按权值插入,维护区间最小值,第x颗线段树,区间l,r表示l到r在1到x出现最后的最早一个是哪个位置

 

 

 

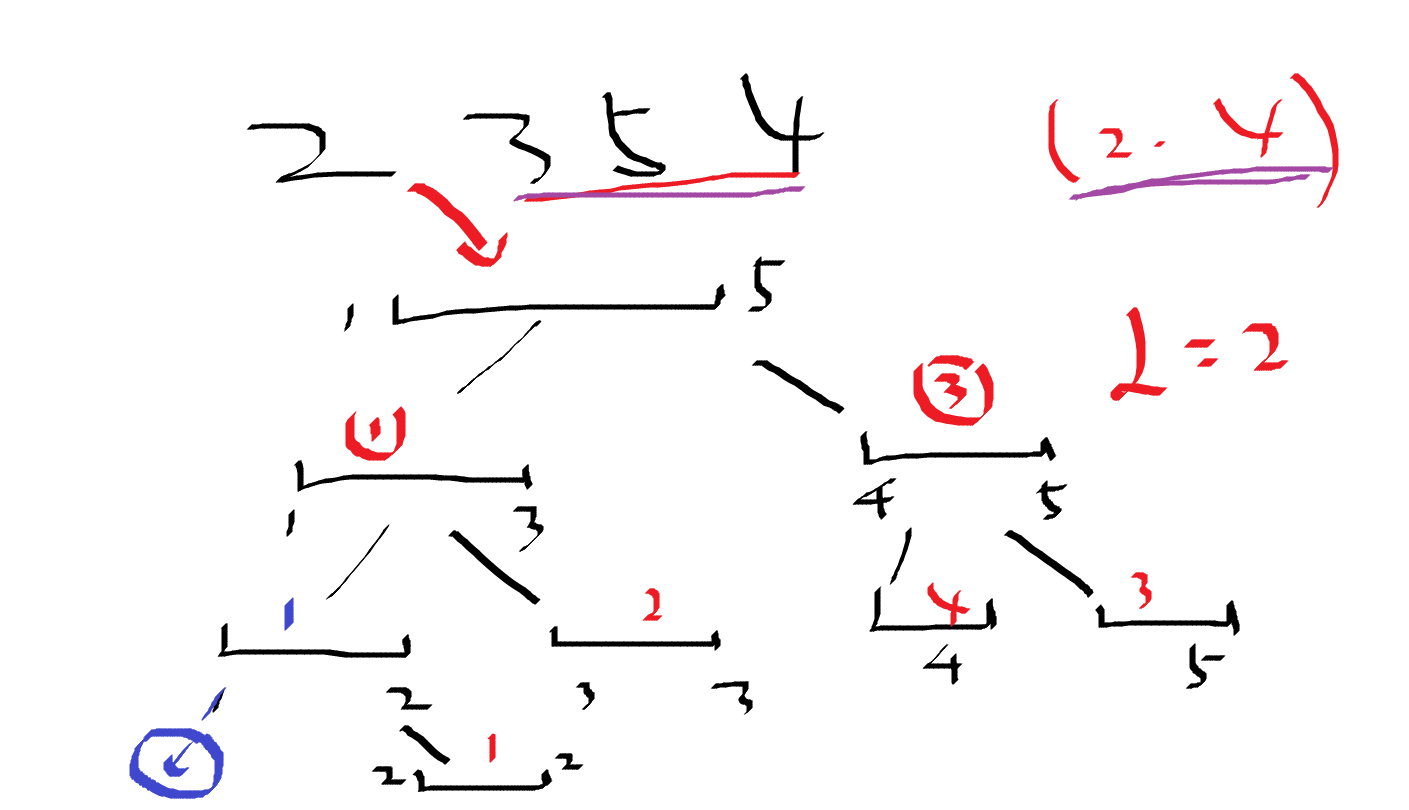
因为是找没出现的最小非负数，其包含了0
所以给所有读入的数字加1

维护数字出现的位置
当询问区间[2,4]时
左子树出现的数字的最小位置为1，其并没有大于等于2
而右子树出现的数字的最小位置为3，而3是大于等于2的
说明结果落在左子树

然后到描述区间[1..3]这个树
发现左子树并没有大于等于2

再到区间[1..2],发现左子树并没有大于等于2
再到其左子树[1.1],找到结果

最终为找到的结果再减去1 ，得到0

 

 

备注：

此题虽然读入的a[i]的值很大，但一段区间的mex是<=N+1的。

所以a[i]的值可以很大，但仍可加入到权值线段树中，例如将数字6，加入到值域为[1..5]之间的权值线段树中，这样6会加到5的那个位置，并且，它也不是成为答案。

 

其实也可以维护区间出现的数字个数，与区间值域是否相等。

例如区间[1..5]出现了多少个数字，如果没有5个数字，就说明少了一个数字。。。

#include<bits/stdc++.h>
#define fio ios::sync_with_stdio(false);cin.tie(0)
template<typename T>inline T const& MAX(T const &a,T const &b) {
	return a>b?a:b;
}
template<typename T>inline T const& MIN(T const &a,T const &b) {
	return a<b?a:b;
}

using namespace std;

const long long INF=0x3f3f3f3f3f3f3f3f;
const int N=200000+10,maxn=200000+10,inf=0x3f3f3f3f;

int a[N],root[N*20],ls[N*20],rs[N*20],mi[N*20],cnt;
void pushup(int o) 
{
	mi[o]=min(mi[ls[o]],mi[rs[o]]);
}
void update(int last,int &o,   int pos,   int v,int l,int r) 
//   update(root[i-1],root[i], a[i],      i,      1,  n);
{
	o=++cnt;
	mi[o]=mi[last];
	ls[o]=ls[last];
	rs[o]=rs[last];
	if(l==r) 
	{
		mi[o]=v;
		return ;
	}
	int m=(l+r)>>1;
	if(pos<=m)
	    update(ls[last],ls[o],pos,v,l,m);
	else 
	    update(rs[last],rs[o],pos,v,m+1,r);
	pushup(o);
}
int query(int o,int v,int l,int r) 
{
	if(l==r)return l;
	int m=(l+r)>>1;
	if(mi[ls[o]]>=v)
	    return query(rs[o],v,m+1,r);
	else 
	    return query(ls[o],v,l,m);
}
int main() {
	int n,m;
	scanf("%d%d",&n,&m);
	for(int i=1; i<=n; i++) 
	{
		scanf("%d",&a[i]);
		a[i]++;
		update(root[i-1],root[i],a[i],i,1,n);
	}
	while(m--) {
		int l,r;
		scanf("%d%d",&l,&r);
		printf("%d\n",query(root[r],l,1,n)-1);
	}
	return 0;
}