树的染色

 

Description
有一个N个结点的有根树，R是这个树的根。

现在要对这N个结点依次进行染色，每个结点染色要花费1个单位的时候，

同时要满足一个结点仅在其父亲被染色后才可被染色，每个结点有个权值Ci,

如果我们在第Ti时间对i号结点染色，则付出总代价为Sigma(Ti*Ci),1<=i<=N.

现在给出这个树和每个点的权值，请构造一种染色顺序，使得总代价最小.

Format
Input
第一行正整数N.R

第二个给出N个数字，代表每个点的权值ci

接下来N-1描述这个树

Output
最小的总代价

Samples
输入数据 1
4 1
1 3 2 6
1 2
1 3
2 4
输出数据 1
33
Hint

先染1号点，代价为1 * 1 =1

再染2号点，代价为2 * 3 = 6

再染4号点，代价为3 * 6 =18

再染3号点，代价为4 * 2 =8

总代价为33

 

 

首先明确以下几点：

0:因为先要染根，再来染其它点。所以我们先假设根被染过了。代价量是多少先不管。

1:当需要对某个点进行染色的时候，必然是其父亲点被染过了，才来染它的

2:如果某个点有父亲点，有兄弟点，则有可能是染完父亲点，再染兄弟点，再来染它
为了记录下染的“序号”，即它是第几个被染的，我们可以将兄弟点被染过后，将兄弟点所在块的个数加到父亲点上。
这样就好了。

3：如果是先染树中间的某一个点，则将这个点并到它父亲点上去，并且将它的子结点全变成它父亲的子结点。

于是：

经过上述操作，根下面的各个子树，会变成一砣砣的“合并点”

 

接下来，我们必须找出一种染的策略，则先染谁，再染谁。
不妨设1为根，其左子树总权值为Vy,总点数为Sy,其右子树总权值为Vx,总点数为Sx,

 

 

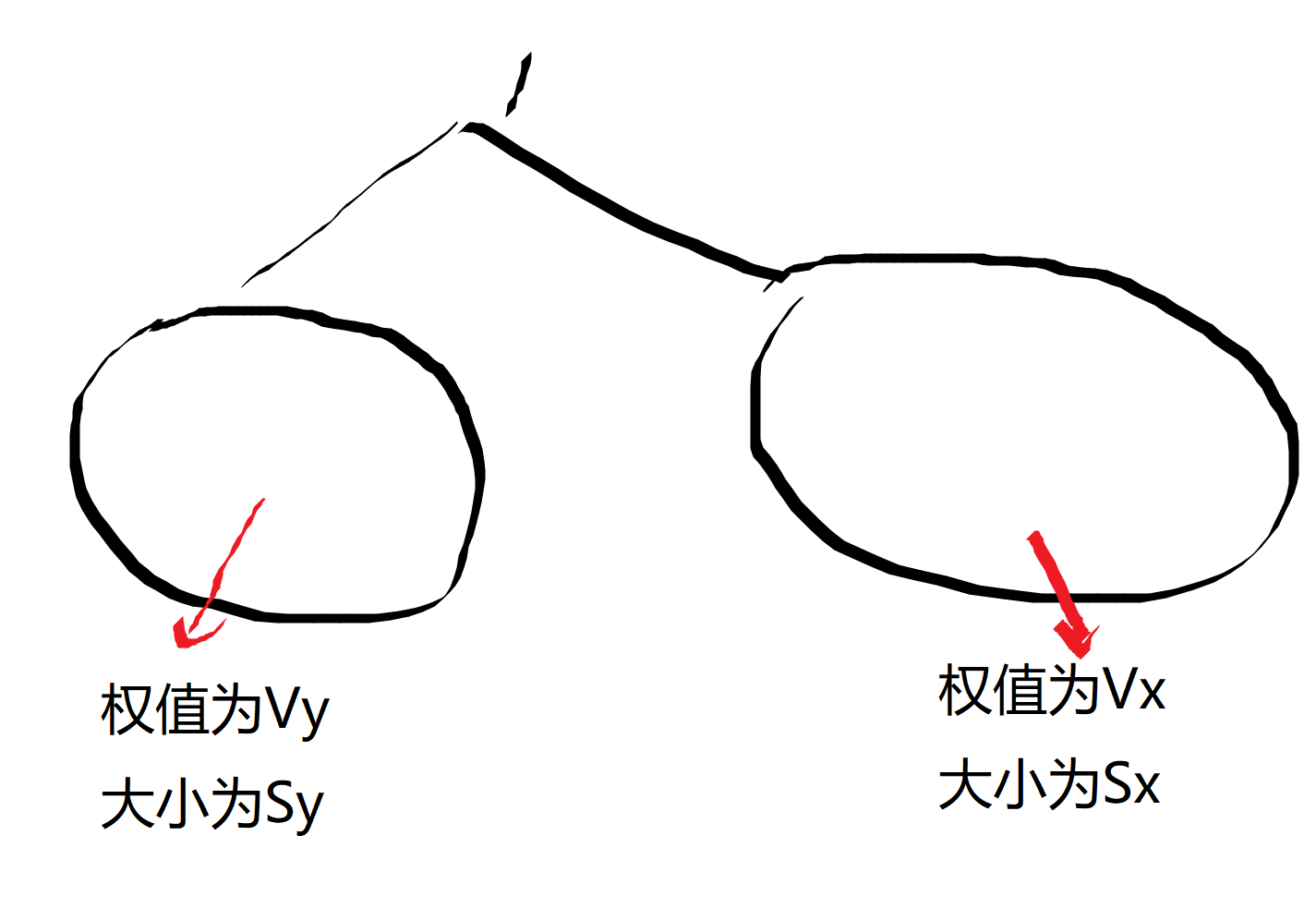
如果先左再右，则总代价为
1*vy+(Sy+1)*Vx
如果先右再左，则总代价为
1*Vx+(Sx+1)*Vy
如果前者更优
则
Vy+(Sy+1)*Vx<Vx+(Sx+1)*Vy
SyVx<SxVy
Vx/Sx<Vy/Sy
即哪个块的总权值/总点数更大，谁就应该被先染.

拿数据
4 1
1 3 2 6
1 2
1 3
2 4

 

 

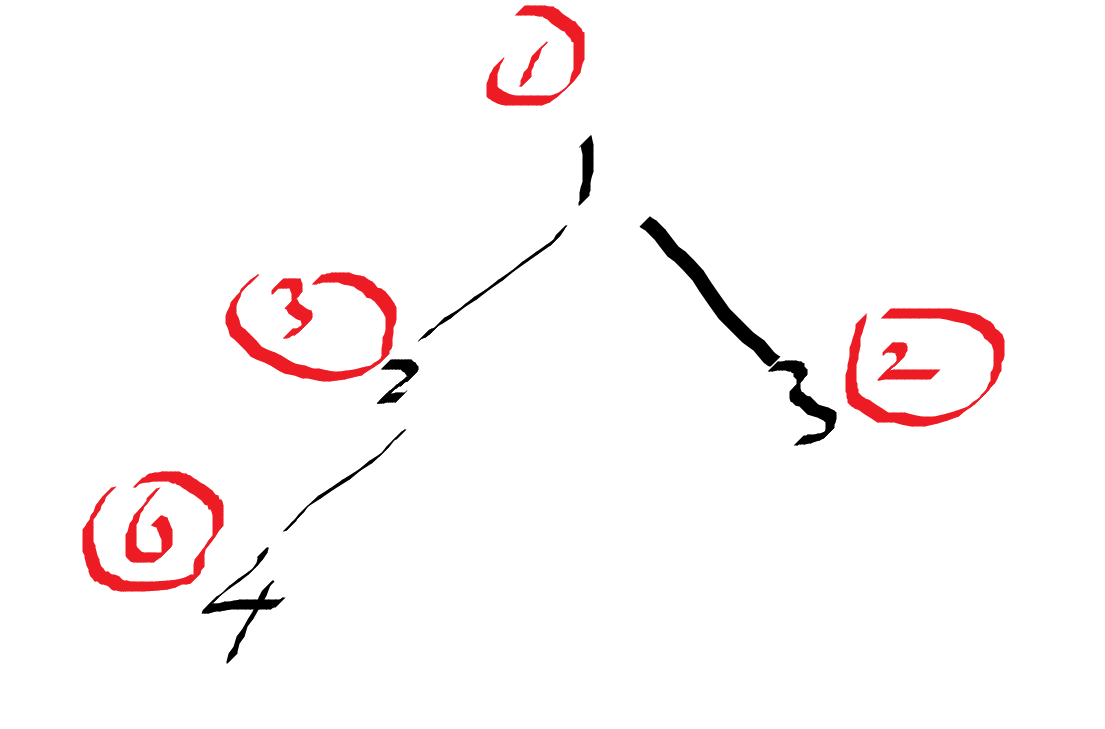
来说

先令每个点权值为其自身权值，块大小为1
先染4，代价为6*1，其中6为其自身权值，1为其父亲点2的块的大小。
染完后，将4的权值及块大小，并到2中去。
再染2，代价为9*1，其中9为其自身权值，1为其父亲点1的块的大小。
染完后，将2的权值及块大小，并到1中去。
再染3，代价为2*3，其中2为其自身权值，3为其父亲点1的块的大小。
染完后，将3的权值及块大小，并到1中去。
最后一次，代价为所有点权值之和*1，1相当于1的父亲点0的大小。

最终结果为（下式中的乘法，都是权值在前，次数在后）

6*1+(6+3)*1+2*3+(1+2+3+6)*1
=1*1+3*2+6*3+2*4
即按1,2,4,3这样的顺序染下来。

 

 最后我们要将最开始少加的量加上去，即在染根的时候，其代价值应该是所有点之和。

因为在后面的计算中，我们都会对每个点染的时间点提前1个时间点。

即本来是第二个被染色的，但是我们算成了第1个被染色的了。

于是这个量都要在最后加进来。。

 

当然我们也可以理解成最后所有点并在根那去了

然后根的上面还有一个父亲点0号点，0号点的大小为1.。。

 

#include<bits/stdc++.h>
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
int n,r,x,y,fa[1010],v[1010];
double t[1010];
int main()
{
        scanf("%d%d",&n,&r);
        int ans=0,sum;
        double mx;
        for(int i=1;i<=n;i++)
        {
            scanf("%d",&v[i]);
            ans+=v[i];  //假设每个点都被首先染色过
            t[i]=1;
        }
        for(int i=1;i<n;i++)
        {
            scanf("%d%d",&x,&y);
            fa[y]=x;
        }
        for(int i=1;i<=n;i++)
        {
            mx=sum=0;
            for(int j=1;j<=n;j++)
            if(v[j]/t[j]>mx&&j!=r)
                    mx=v[j]/t[j],sum=j;
            ans+=v[sum]*t[fa[sum]];
             //取出这个点的权值，及它父亲点的t值，注意是父亲点的..
             //也就是说当它父亲点染过后，它才被染，所以父亲点所在连通块有多少个点，它被染的序号就是乘上多少
            v[fa[sum]]+=v[sum];
            t[fa[sum]]+=t[sum];
            v[sum]=0;
            for(int j=1;j<=n;j++) //将所有点，如果其父亲从前是sum,现在的父亲点改为fa[sum]
                if(fa[j]==sum)
                   fa[j]=fa[sum];
       
        }
        printf("%d\n",ans);
   
    return 0;
}

　　

 

数据加强版在这

[HNOI/AHOI2018]排列

 

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=1000010;
int n,a[N],w[N],head[N],nxt[N],to[N],num=0,in[N],fa[N];
inline void link(int x,int y){nxt[++num]=head[x];to[num]=y;head[x]=num;}
inline bool topsort(){
    queue<int>Q;
    Q.push(0);
    while(!Q.empty()){
        int x=Q.front();Q.pop();
        for(int i=head[x];i;i=nxt[i]){
            int u=to[i];
            if(!(--in[u]))Q.push(u);
        }
    }
    for(int i=1;i<=n;i++)if(in[i]>0)return false;
    return true;
}
struct data{
    ll w;int s,x;
    bool operator <(const data &p)const{
        if(w*p.s!=p.w*s)return w*p.s<p.w*s;
        return x<p.x;
    }
}p[N];
set<data>Q;
int cnt=0,b[N];
inline int find(int x){return b[x]==x?x:b[x]=find(b[x]);}
int main(){
  scanf("%d",&n);
  for(int i=1;i<=n;i++)
        scanf("%d",&a[i]),link(a[i],i),in[i]++,fa[i]=a[i];
  for(int i=1;i<=n;i++)scanf("%d",&w[i]);
  if(!topsort()){puts("-1");return 0;}
  for(int i=1;i<=n;i++){
      p[i]=(data){w[i],1,i};
      Q.insert(p[i]);b[i]=i;
  }
  cnt=n;p[0].s=1;
  ll ans=0;
  data t;
  while(!Q.empty()){
      t=*Q.begin();Q.erase(t);
      int y=find(fa[t.x]);
      ans+=t.w*p[y].s;
      if(y){
          Q.erase(p[y]);
          data e=t;
          e.w+=p[y].w;e.s+=p[y].s;e.x=++cnt;
          b[cnt]=cnt;b[y]=cnt;b[find(t.x)]=cnt;
          fa[cnt]=fa[y];fa[t.x]=cnt;
          p[cnt]=e;
          Q.insert(e);
      }
      else b[find(t.x)]=0,p[0].s+=t.s;
  }
  cout<<ans<<endl;
  return 0;
}