单调队列优化多重背包问题 + 例题

 例题：https://www.acwing.com/problem/content/6/

 

 

有 N 种物品和一个容量是 V 的背包。

第 i 种物品最多有 si 件，每件体积是 vi，价值是 wi。

求解将哪些物品装入背包，可使物品体积总和不超过背包容量，且价值总和最大。
输出最大价值。

输入格式
第一行两个整数，N，V (0<N≤1000, 0<V≤20000)，用空格隔开，分别表示物品种数和背包容积。

接下来有 N 行，每行三个整数 vi,wi,si，用空格隔开，分别表示第 i 种物品的体积、价值和数量。

输出格式
输出一个整数，表示最大价值。

数据范围
0<N≤1000
0<V≤20000
0<vi,wi,si≤20000

输入样例
4 5
1 2 3
2 4 1
3 4 3
4 5 2
输出样例：
10

 

https://blog.csdn.net/weixin_43191865/article/details/100108582?spm=1001.2101.3001.6650.1&utm_medium=distribute.pc_relevant.none-task-blog-2~default~CTRLIST~default-1.highlightwordscore&depth_1-utm_source=distribute.pc_relevant.none-task-blog-2~default~CTRLIST~default-1.highlightwordscore

 https://www.cnblogs.com/-guz/p/9866118.html

Sol:

正常的多重背包的dp方程：
dp[i][k]=max(dp[i-1][s]+(k-s)/v*w,dp[i][k])
k代表一共使用的空间
s代表前i-1个物品占用的空间
(k-s)为第i个物品占用的空间
v为第i个物品的体积，w为其权值

对于K来说，其决策点与K之间的差必然为v的若干倍
也就是说
如果k=12,v=3
则K是从体积为3,6,9这样的点转移过来的。
如果k=15
则K是从体积为3,6,9,12这样的点转移过来的。

于是将K进行分类,分类的依据就是当前物品的体积v
任何数字mod v只有J种可能，从0 到v-1
对于每一类，开一个单调队列出来.

也就是说我们从前的计算是从小到大枚举K，按顺序算过去。

现在则是一段一段的算，仍以物品体积为3来说

先算0,3,6,9,12......

再算1,4,7,10,13.......

再算2,5,8,11,14........

总的时间复杂度为O(n∗V)

 

 

 

 

 

 

 

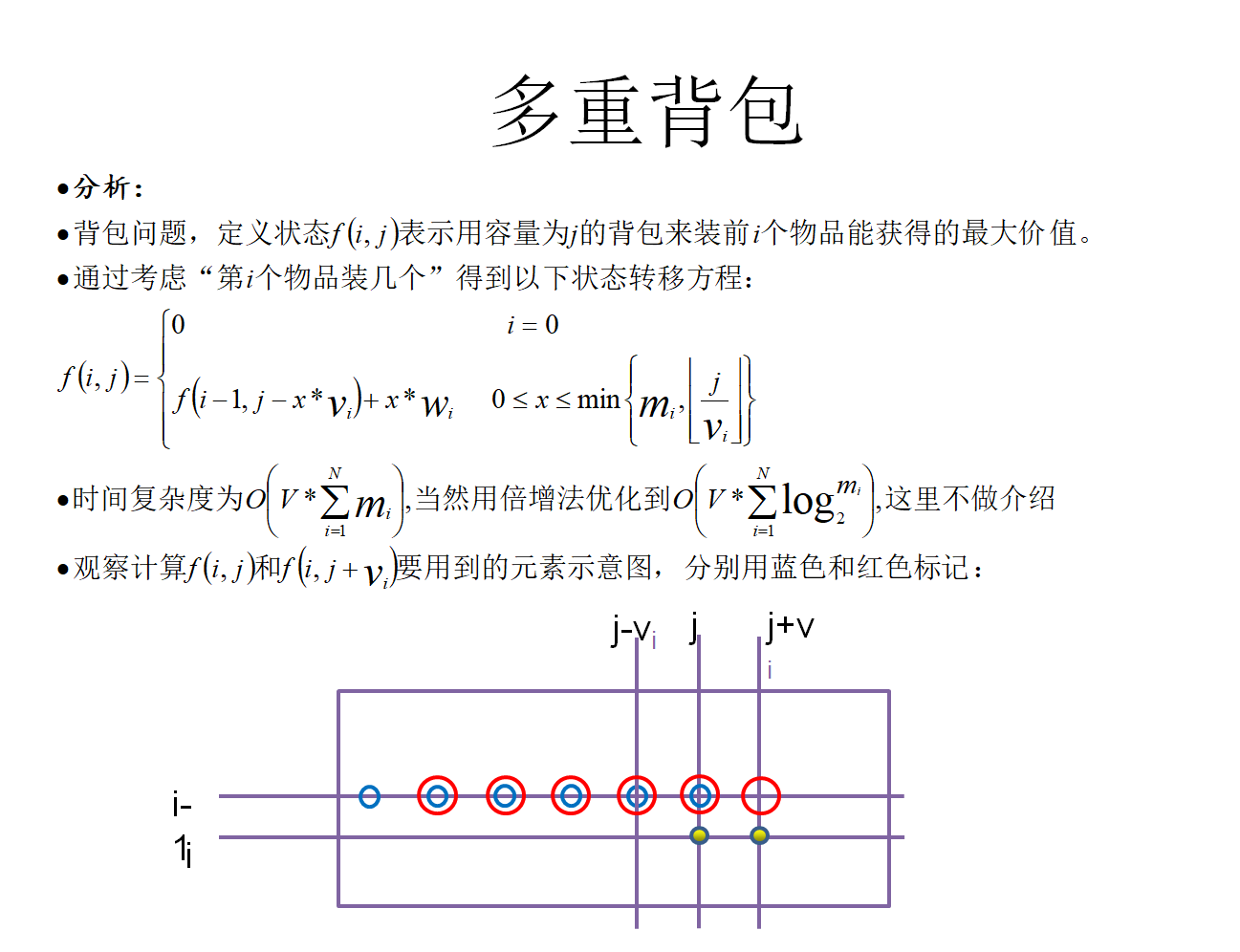
计算f[i,j]有两个可选决策x1,x2
如果x2>x1时，下面条件如果成立
f(i-1,j-x2*vi)+x2*Wi>=f(i-1,j-x1*vi)+x1*Wi
则当我们计算状态j+k*Vi时
这两个决策点也可平移至x1+k,x2+k
而式1
f(i-1,j+K*Vi-(x2+k)*vi)+(x2+k)*Wi
=f(i-1,j-x2*vi)+(x2+k)*Wi

仍大于式2
f(i-1,j+K*Vi-(x1+k)*vi)+(x1+k)*Wi
=f(i-1,j-x1*vi)+(x1+k)*Wi

 

 

#include<bits/stdc++.h>
using namespace std;
const int maxn = 2e4 + 7;
int dp[2][maxn], q[maxn]; // dp 为滚动数组， q为优先队列辅助数组
#define calc(t,i) (dp[t^1][q[i]]+((k-q[i])/v)*w)
int main() {
	int n, m;
	cin >> n >> m;
	//N个物品，M为总体积 
	int t = 0;
	for (int i = 1; i <= n; i++) 
	{
		int v, w, s;
		scanf("%d %d %d", &v, &w, &s);
		//v--体积,w--价值,s--数量 
		t ^= 1; //数组滚动
		for (int j = 0; j < v; j++) 
		//枚举余数 
		{
			int l = 1, r = 0;
			for (int k = j ; k <= m; k += v) 
			//所占用的体积,k与j是同余的. 
			{
				while (l <= r && (k-q[l])/v > s) 
				        l++; // 排除太远的，其超过了能提供的份数了
				if(l<=r) 
			        dp[t][k] = max(dp[t^1][k], calc(t,l));
				while (l <= r && dp[t ^ 1][q[r]] - (q[r] - j) / v * w <= dp[t ^ 1][k] - (k - j) / v * w)
				        r--;//消除距离影响
				q[++r] = k;
			}
		}
	}
	cout << dp[t][m] << endl;
	return 0;
}