黑暗城堡

在顺利攻破Lord lsp的防线之后，lqr一行人来到了Lord lsp的城堡下方。Lord lsp黑化之后虽然拥有了强
大的超能力，能够用意念力制造建筑物，但是智商水平却没怎么增加。现在lqr已经搞清楚黑暗城堡有N个房间
，M条可以制造的双向通道，以及每条通道的长度。lqr深知Lord lsp的想法，为了避免每次都要琢磨两个房间
之间的最短路径，Lord lsp一定会把城堡修建成树形的；但是，为了尽量提高自己的移动效率，Lord lsp一定会
使得城堡满足下面的条件：设Di为如果所有的通道都被修建，第i号房间与第1号房间的最短路径长度；而Si
为实际修建的树形城堡中第i号房间与第1号房间的路径长度，对于所有满足1≤i≤N的整数i，有Si=Di
。为了打败Lord lsp，lqr想知道有多少种不同的城堡修建方案。于是lqr向applepi提出了这个问题。由于a
pplepi还要忙着出模拟赛，所以这个任务就交给你了。当然，你只需要输出答案对2^31–1取模之后的结果就
行了.
Input
第一行有两个整数N和M。
之后M行，每行三个整数X，Y和L，表示可以修建X和Y之间的一条长度为L的通道。
2≤N≤1000，N–1≤M≤N(N–1)/2，1≤L≤100
Output
输出一个整数，表示答案对2^31–1取模之后的结果。

Sample Input
3 3
1 2 2
1 3 1
2 3 1
Sample Output
2

Sol:

此题要求找出有多少种最短树径生成树

则设出发点为1.于是1到它之前的点，也就是它自己有1种方式

然后对于点J，2<=j<=N,其实就是找J有多少种方式连向它左边的点，即最短路小于J的最短路的点。

最后乘起来即可。

 

 

于是在跑最短路的时候，每当找到一个中转点mini,它使用它进行迭代更新点J的时候

如果发现找到了一条新的最短路，则j有一种方式连向它前面的点（这个前面是指最短路的值小于J的）

如果新路径与J从前的最短路一样，则加加即可。

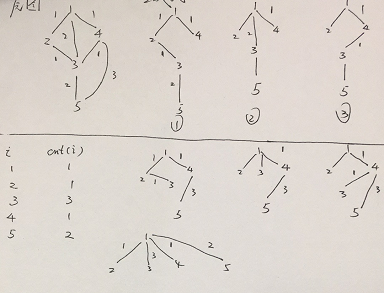
拿上面这个图来说

最开始找到中转点为1，于是在更新2，3，4的最短路的时候，这三个点都可以有1种方式连向前面的点

然后找到中转点2，在更新3的时候，3又可以与2相连，多了一种方式

然后找到中转点4，在更新3的时候，3又可以与4相连，多了一种方式，在更新5的时候，5可以与4相连。。。

 

 

 

 

 

跑一次最短路，同时记下从1出发到每个点的最短图，并统计出有多少条。在构建后面的最短路径树时，乘起来就好了。

 

#include <bits/stdc++.h>
 
using namespace std;
typedef long long ll;
const int maxn = 1e3 + 100;
const int inf = 0x3f3f3f3f;
const int mod = (1 << 31) - 1;
int mapp[maxn][maxn];
int vis[maxn], dis[maxn],sum[maxn];
int n, m;
struct node {
    int id, d;
} s[maxn];
 
bool cmp(node a, node b) 
{
    return a.d < b.d;
}
 
void dij() 
{
    memset(vis, 0, sizeof(vis)); //每个点都没有找到最短路 
    memset(dis, 0x3f, sizeof(dis));  //每个点到1的距离为无限大 
    dis[1] = 0;
    sum[1]=1;
    for (int i = 1; i < n; i++) 
	{
        int p = 0;
        for (int j = 1; j <= n; j++) 
		{
            if (!vis[j] && (p == 0 || dis[j] < dis[p])) 
			    p = j; //找出一个中转点P出来  
        }
        vis[p] = 1;  //打上标志，代表P已经充当过中转点了 
        for (int j = 1; j <= n; j++) //更新其它点到1的最短路 
        if (vis[j]==false) //如果这个点没有更新过 
            if (dis[j]>dis[p] + mapp[p][j])
            //找到一个新的最短路，可以从从前的某个点连接起来 
                  {
                         dis[j]=dis[p] + mapp[p][j];
                         sum[j]=1;
                  }  
            else
                if (dis[j]==dis[p] + mapp[p][j])
                //又多了一个点 
                    sum[j]=sum[j]+1;
}
}
int main() {
 
    scanf("%d%d", &n, &m);
    memset(mapp, 0x3f, sizeof(mapp));
    int u, v, c;
    for (int i = 1; i <= m; i++) 
	{
        scanf("%d%d%d", &u, &v, &c);
        mapp[u][v] = mapp[v][u] = min(mapp[u][v], c);
    }
    dij();
    ll ans = 1;
    for (int i = 1; i <= n; i++) 
	{
         if (sum[i]!=0)
                ans = ans * sum[i] % mod;
    }
    printf("%lld\n", ans);
    return 0;
}

　　

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
#include<cmath>
#include<map>
#include<queue>
#include<set>
#define ll long long
#define llu unsigned ll
using namespace std;
const int mod=(1ll<<31)-1;
const int maxn=1000100;
const int maxx=1200;
const int inf=0x3f3f3f3f;
int head[maxx],edge[maxn],ver[maxn],nt[maxn];
int d[maxx];
int ha[maxx];
int cnt[maxx];
int tot=1,n,m;
void add(int x,int y,int z)
{
    ver[++tot]=y,edge[tot]=z;
    nt[tot]=head[x],head[x]=tot;
}
void Dij(void)
{
    memset(d,0x3f,sizeof(d));
    memset(ha,0,sizeof(ha));
    d[1]=0;
    priority_queue<pair<int,int> >q;
    q.push(make_pair(0,1));
    while(q.size())
    {
        int x=q.top().second;
        q.pop();
        if(ha[x]) continue;
        ha[x]=true;
        for(int i=head[x];i;i=nt[i])
        {
            int y=ver[i],z=edge[i];
            if(d[y]>d[x]+z) //更新最短路 
            {
                d[y]=d[x]+z;
                cnt[y]=1;//从出发点到y的最短路有1条了 
                q.push(make_pair(-d[y],y));
            }
            else if(d[y]==d[x]+z)//找到另一条到y的最短路 
            {
                cnt[y]++;
            }
        }
    }
    return ;
}
int main(void)
{
    scanf("%d%d",&n,&m);
    int x,y,z;
    for(int i=1;i<=m;i++)
    {
        scanf("%d%d%d",&x,&y,&z);
        add(x,y,z);
        add(y,x,z);
    }
    Dij();
    cnt[1]=1;
    ll ans=1;
    for(int i=1;i<=n;i++)
    {
		//cout<<i<<"   "<<cnt[i]<<endl;
        ans=ans*cnt[i]%mod;
    }
    printf("%lld\n",ans);
    return 0;
}

input 

5 7
1 2 1
1 3 2
1 4 1
2 3 1
4 3 1
3 5 2
4 5 3

output
6