电梯调度问题
题目在qoj上,原题是英文的
https://qoj.ac/problem/8142
用户名: linyide 密码 : qwer1234
题目描述
一栋 $ m $ 层的楼里有 $ n $ 架电梯,标号分别为 $ 1 \sim n $。
初始所有电梯都在第 1 层,第 $ i $ 架电梯会在时刻 $ a_i $ 启动,电梯启动后每个时刻会上升 1 层。
你可以在一开始按下 $ 2 \sim m $ 中一些楼层的按钮,这会使第一个到达这个楼层的编号最小的电梯在这一层停留一个时刻。
对于每架电梯,输出最少要按多少个楼层的按钮才能使它第一个登顶。(若同时登顶,则它需要是编号最小的)
输入格式
第一行两个整数 $ n, m $。
接下来一行 $ n $ 个整数表示 $ a_{1 \sim n} $。
输出格式
输出 $ n $ 个整数,每个数占一行,第 $ i $ 个整数表示让第 $ i $ 架电梯最先登顶的最小按键数,如果无论如何它都无法第一个登顶,输出 -1。
输入输出样例
输入1
4 14
25 18 30 31
输出1
7
0
-1
-1
输入2
6 20
3 8 12 6 9 9
输出2
0
8
-1
4
13
14
数据范围
- 对于 10% 的数据,$ n = 2 $
- 对于 30% 的数据,$ n, m \leq 300 $
- 对于 50% 的数据,$ m < 5000 $
- 存在另外 20% 的数据,$ a_i < 50 $
- 对于 100% 的数据,$ 1 < n < 5 \times 10^5 , 1 < m < 10^9 , 1 < a_i < 10^9 $
解析
手工模拟测试样例,就可以找出规律。为了让第 i 架电梯成为“第一名”,我们需要通过按按钮(增加延迟),使得所有原本比它早出发的电梯最终都比它慢。具体分为2种情况:
- 对于 \(j < i\):如果 \(a_j \le a_i\),则 \(j\) 必须被拖慢到至少 \(a_i + 1\) 的时刻。所需代价为 \(a_i - a_j + 1\)。
- 对于 \(j > i\):如果 \(a_j \le a_i\),则 \(k\) 必须被拖慢到至少 \(a_i\) 的时刻。所需代价为 \(a_i - a_j\)。
将所有电梯按 \(a_i\) 从小到大排序,按排序顺序对每个电梯求按键次数 \(R_i\):
\[R_i=\sum_{a_j\le a_i}(a_i-a_j)+\#\{j<i \mid a_j\le a_i\}
\]
\[其中 \#\{j<i \mid a_j\le a_i\} 表示已经处理过的、下标 ≤ x 的电梯个数,可以用树状数组统计
\]
参考代码
#include <bits/stdc++.h>
using namespace std;
// 使用 long long 防止按键总数累加时溢出
// 因为 tot 可能会变得非常大
#define int long long
#define endl '\n'
const int MAXN = 1e6 + 5;
const int INF = 0x3f3f3f3f3f3f3f3f;
// 树状数组 (Fenwick Tree) 数组
// tr[i] 将用来存储电梯的“原始编号”出现的次数
vector<int> tr(MAXN);
void solve()
{
int n, m;
cin >> n >> m;
// --- 树状数组基础函数 ---
// lowbit: 获取二进制最低位的 1
auto lowbit = [&](int x) -> int
{
return x & (-x);
};
// add: 单点修改,在位置 x 加上 v
// 这里用于将某个电梯的编号加入集合
auto add = [&](int x, int v)
{
for (int i = x; i <= n; i += lowbit(i))
tr[i] += v;
};
// query: 前缀求和,查询 [1, x] 的总和
// 这里用于查询有多少个已处理的电梯编号小于等于 x
auto query = [&](int x)
{
int sum = 0;
for (int i = x; i; i -= lowbit(i))
sum += tr[i];
return sum;
};
// a: 存储初始启动时间
// pos: 存储电梯的原始编号,用于排序后追踪是谁
// ans: 存储最终答案
vector<int> a(n + 1), pos(n + 1), ans(n + 1);
for (int i = 1; i <= n; ++i)
{
cin >> a[i];
pos[i] = i; // 初始化原始编号
}
// --- 核心步骤 1: 排序 ---
// 按照“谁最先登顶的自然优势最大”进行排序。
// 优先按启动时间 a[x] 从小到大排(越早启动越快)。
// 如果时间相同,按原始编号 x 从小到大排(编号小有优先权)。
sort(pos.begin() + 1, pos.end(), [&](int x, int y)
{
if(a[x] != a[y])
return a[x] < a[y];
return x < y;
});
// --- 处理排名第 1 的电梯 ---
// 它是最快的,天然就是第一名,不需要按键。
ans[pos[1]] = 0;
// 将它的原始编号加入树状数组,表示这个编号的对手已经出现过
add(pos[1], 1);
int tot = 0; // tot: 记录将前面所有电梯拖慢到“当前处理电梯的时间”所需的总按键数
// --- 核心步骤 2: 线性扫描 ---
// 从排名第 2 的电梯开始遍历到最后一名
for (int i = 2; i <= n; i++)
{
// a[pos[i]]: 当前电梯的启动时间
// a[pos[i-1]]: 上一个(比当前略快或同速)电梯的启动时间
// 差值 diff = a[pos[i]] - a[pos[i-1]]
// 既然 pos 数组已经排好序了,说明前面 i-1 个电梯原本都比当前电梯快(或同速)。
// 为了让当前电梯 pos[i] 有机会赢,我们至少得把前面那 i-1 个电梯都拖慢到和 pos[i] 同一个起跑线。
// 所以,前面的 i-1 个电梯,每个人都需要增加 diff 的等待时间。
tot += (a[pos[i]] - a[pos[i - 1]]) * (i - 1);
// --- 计算最终代价 ---
// ans[pos[i]] 由两部分组成:
// 1. tot: 基础代价。把所有对手的时间都拉平到了 a[pos[i]]。
// 2. query(pos[i]): 额外代价。
// 现在所有强力对手的时间都和当前电梯一样了。
// 根据规则:时间相同时,编号小的优先。
// 如果我们(pos[i])的编号比对手大,那就算时间一样,我们也输了。
// 所以,必须对那些“编号比 pos[i] 小”的对手再多按 1 次键,让它们比我们慢 1 秒。
// query(pos[i]) 就是在已处理的电梯中,查找编号小于 pos[i] 的数量。
ans[pos[i]] = tot + query(pos[i]);
// 将当前电梯的编号加入树状数组,供后续更慢的电梯计算时将其视为对手
add(pos[i], 1);
}
// --- 输出 ---
// 有效按键层数为 2 到 m-1,共 m-2 层。 第m层按已经太迟了
// ans[i] > m - 2 时输出 -1。
for (int i = 1; i <= n; i++)
cout << (ans[i] > m - 2 ? -1 : ans[i]) << endl;
}
signed main()
{
// 开启 IO 优化
ios_base::sync_with_stdio(0);
cin.tie(0);
int T = 1;
// cin >> T; // 如果有多组数据解开注释
while (T--)
{
solve();
}
return 0;
}
关键代码:
tot += (a[pos[i]] - a[pos[i - 1]]) * (i - 1);
这是一个巧妙而重要的数学技巧。
它的作用:
维护下面这个值:
\[\sum_{k=1}^{i-1}(a[pos[i]] - a[pos[k]])
\]
也就是:
当前电梯 “与之前所有电梯的差值和”
为什么这么更新?
假设 a 排序后为:
a1 ≤ a2 ≤ a3 ≤ ... ≤ an
对于 ai:
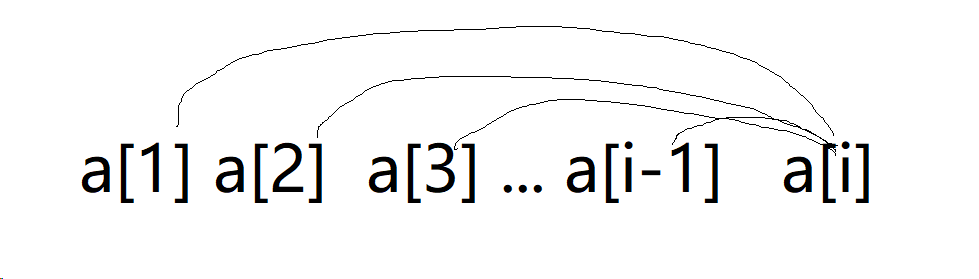
\[\sum_{k < i} (a_i - a_k) = (a_i - a_{i-1})*(i-1) + (a_{i-1}-a_{i-2})*(i-2)+...
\]
所以写成差分方式:
当 i 增加到 i+1:
\[\Delta = (a_{i+1}-a_i) * (i)
\]
这就是:
tot += (a[pos[i]] - a[pos[i-1]]) * (i - 1);
(4)最终答案:
ans[pos[i]] = tot + query(pos[i]);
query(pos[i])也就是编号更小且值不大的电梯数量(这些电梯需要额外 +1 延迟,因为编号小要严格被压过)。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号