B3611 【模板】传递闭包
传递闭包两种写法,bitset方法必须理解掌握
B3611 【模板】传递闭包
https://www.bilibili.com/video/BV1sM411Z7d6
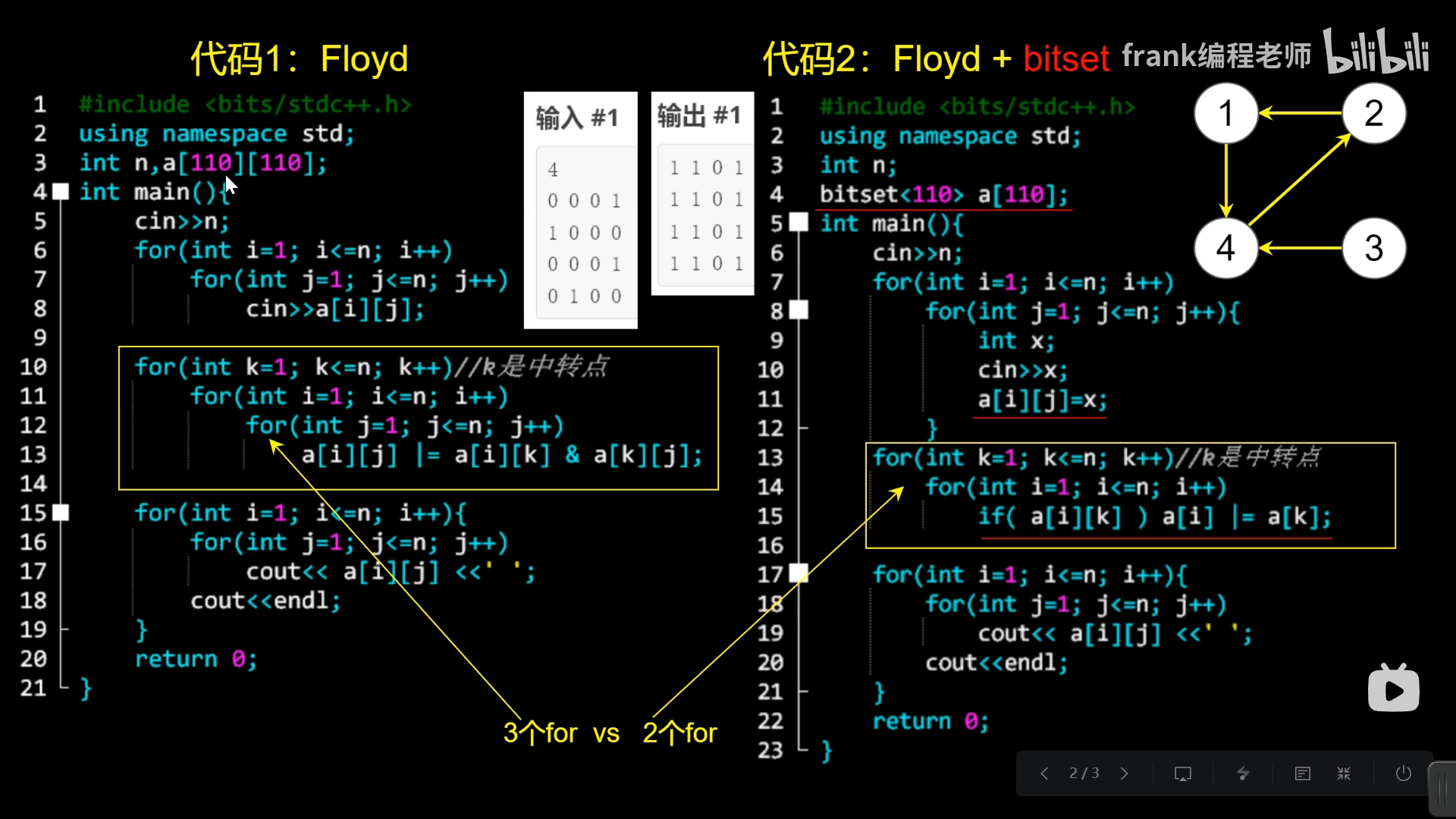
传递闭包加强版本
算法思路
1️⃣ 本质:求每个点的可达集合
这道题要求的是:
\[\text{Ans} = \sum_{i=1}^n |\text{reachable}(i)|
\]
也就是说,我们要知道「从 i 出发能到哪些点」。
2️⃣ 直接 Floyd 太慢!
普通 Floyd 算法是 \(O(n^3)\) ,
而这里 \(n \le 2000\) , \(2000^3 = 8 \times 10^9\) ,根本不可行。
我们需要优化!
3️⃣ 关键优化:位集(bitset)优化传递闭包
思路:
- 把每一行的邻接关系(可达性)用
bitset<N>来表示; - 然后模拟传递闭包的思想(类似 Floyd):
对于每个中间点 \(k\) :
如果 \(i\) 可以到达 \(k\) ,那么 \(i\) 也可以到达所有 \(k\) 能到的点。
也就是说:
\[\text{reachable}[i] |= \text{reachable}[k]
\]
代码上就是:
if (reach[i][k])
reach[i] |= reach[k];
这样复杂度从 \(O(n^3)\) 优化成了大约 \(O(\frac{n^3}{w})\) ,
其中 \(w=64\) (一个 unsigned long long 有 64 位)
4️⃣ 算法流程总结
- 读入邻接矩阵;
- 初始化
reach[i][j]; - 自己能到自己:
reach[i][i] = 1; - 位集优化版传递闭包:
for k in 1..n: for i in 1..n: if reach[i][k]: reach[i] |= reach[k]; - 统计所有
reach[i]的 1 的个数之和。
C++ 实现(OI风格 + 详细注释)
#include <bits/stdc++.h>
using namespace std;
const int N = 2005;
bitset<N> reach[N]; // reach[i][j] 表示 i 是否能到 j
int n;
int main() {
ios::sync_with_stdio(0);
cin.tie(0);
cin >> n;
for (int i = 1; i <= n; i++) {
string s;
cin >> s;
for (int j = 1; j <= n; j++) {
if (s[j - 1] == '1')
reach[i][j] = 1;
}
reach[i][i] = 1; // 自身可达
}
// Floyd 思想 + 位运算优化
for (int k = 1; k <= n; k++) {
for (int i = 1; i <= n; i++) {
if (reach[i][k]) // 如果 i 可以到 k
reach[i] |= reach[k]; // 那么 i 可达集合扩充为 i + k 的可达集合
}
}
// 统计答案
long long ans = 0;
for (int i = 1; i <= n; i++)
ans += reach[i].count(); // bitset 提供 count() 统计 1 的数量
cout << ans << '\n';
return 0;
}
复杂度分析
- 时间复杂度:
\(O(\frac{n^3}{w}) \approx O(\frac{2000^3}{64}) = 1.25 \times 10^8\) ,可接受。 - 空间复杂度:
\(O(n^2)\) ,约 2000² ≈ 4MB,安全。
总结
| 步骤 | 思想 | 技术点 |
|---|---|---|
| 建图 | 邻接矩阵 | 直接读字符串 |
| 求可达性 | Floyd 传递闭包 | 位运算加速 |
| 统计结果 | bitset.count() | 高效计算 |
用tarjan缩点 + 逆拓扑排序
思路
- 缩点(Tarjan)
把强连通分量(SCC)收缩成一个超点。因为在 SCC 内任意两点互相可达,缩点后超点内部的任意原点可达关系就都包含在一起了。设第 \(i\) 个 SCC 的大小为 \(\text{sz}[i]\) 。 - 构建压缩图(DAG)
原图中若有边 \(u\to v\) ,且它们属于不同 SCC( \(\text{bel}[u]\neq\text{bel}[v]\) ),则在压缩图中加一条边 \(\text{bel}[u]\to\text{bel}[v]\) 。压缩图是有向无环图(DAG)。 - 在 DAG 上求每个超点能到达哪些超点
我们需要对每个超点 \(x\) 求出「能从 \(x\) 到达的所有超点集合」。注意:不同子树可能重合(多个子节点可以到达同一个后代),不能直接把各子节点的「可达数量」相加,那样会重复计数。正确的方法是维护每个超点的可达集合(表示为bitset),按照拓扑序从后往前合并:\[\text{reach}[x] = \{x\}\ \cup\ \bigcup_{(x\to y)} \text{reach}[y] \]使用bitset做集合并(按位或),效率很高。 - 把超点的可达集合转换为原点数目
对于每个超点 \(x\) ,若 \(\text{reach}[x]\) 中包含超点 \(j\) ,则它能到达的原点数增加 \(\text{sz}[j]\) 。设 \(R[x]\) 为超点 \(x\) 能到达的原点总数,则答案就是\[\text{Ans} = \sum_{x} \text{sz}[x] \cdot R[x] \]因为超点 \(x\) 内的每个原点都能到达这 \(R[x]\) 个原点,总计为 \(\text{sz}[x]\cdot R[x]\) 。
复杂度
- Tarjan: \(O(n + m)\) (这里 \(m\) 是边数,原始输入最多 \(n^2\) )。
- 构建压缩图 + 去重: \(O(n + m)\) (用
bitset标记或后处理)。 - 在压缩 DAG 上
bitset合并:每次合并是按位或,复杂度约为 \(O\big(\frac{S^2}{w}\big)\) ,其中 \(S\) 是 SCC 数( \(S\le n\) ), \(w\) 为字长(比如 64)。对 \(n\le 2000\) 的限制下可接受。 - 总体能在题目限制下顺利通过。
完整代码(OI 风格,注释详细)
#include <bits/stdc++.h>
using namespace std;
const int MAXN = 2005; // 最大顶点数(题目给出 n <= 2000)
int n;
// 原图使用邻接表(只存 '1' 的边)
vector<int> g[MAXN];
// --- Tarjan SCC 相关 ---
int dfn[MAXN], low[MAXN], ts = 0;
int stk[MAXN], top = 0;
bool inStack[MAXN];
int bel[MAXN], scc_cnt = 0; // bel[u] = u 所属的 SCC 编号(1..scc_cnt)
int scc_size[MAXN];
void tarjan(int u) {
dfn[u] = low[u] = ++ts;
stk[++top] = u;
inStack[u] = true;
for (int v : g[u]) {
if (!dfn[v]) {
tarjan(v);
low[u] = min(low[u], low[v]);
} else if (inStack[v]) {
low[u] = min(low[u], dfn[v]);
}
}
if (low[u] == dfn[u]) {
++scc_cnt;
int x;
do {
x = stk[top--];
inStack[x] = false;
bel[x] = scc_cnt;
++scc_size[scc_cnt];
} while (x != u);
}
}
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
cin >> n;
for (int i = 1; i <= n; ++i) {
string s;
cin >> s;
for (int j = 1; j <= n; ++j) {
if (s[j-1] == '1') g[i].push_back(j);
}
}
// 1. Tarjan 找 SCC
for (int i = 1; i <= n; ++i)
if (!dfn[i]) tarjan(i);
// 如果整图就是若干 SCC,编号是 1..scc_cnt
if (scc_cnt == 0) {
cout << 0 << "\n";
return 0;
}
// 2. 构建压缩图(SCC 层面)
// 使用 bitset 标记从一个 SCC 到另一个 SCC 是否有边(去重)
static bitset<MAXN> comp_edge[MAXN]; // comp_edge[i][j] = 1 表示 i -> j 有边(i,j 为 SCC 编号)
for (int u = 1; u <= n; ++u) {
int su = bel[u];
for (int v : g[u]) {
int sv = bel[v];
if (su != sv) comp_edge[su].set(sv);
}
}
// 构建压缩图的邻接表以及入度
vector<vector<int>> comp_adj(scc_cnt + 1);
vector<int> indeg(scc_cnt + 1, 0);
for (int i = 1; i <= scc_cnt; ++i) {
for (int j = 1; j <= scc_cnt; ++j) {
if (comp_edge[i].test(j)) {
comp_adj[i].push_back(j);
indeg[j]++;
}
}
}
// 3. 对压缩 DAG 做拓扑排序(Kahn)
queue<int> q;
vector<int> topo; topo.reserve(scc_cnt);
for (int i = 1; i <= scc_cnt; ++i)
if (indeg[i] == 0) q.push(i);
while (!q.empty()) {
int u = q.front(); q.pop();
topo.push_back(u);
for (int v : comp_adj[u]) {
if (--indeg[v] == 0) q.push(v);
}
}
// 4. 使用 bitset 在拓扑序的逆序上合并可达集合
// reach[i] 表示以 SCC i 为起点能到达的 SCC 集合(包含 i 自身)
static bitset<MAXN> reach[MAXN];
// 先全部清零(静态数组一般初始为 0,但显式写更清晰)
for (int i = 1; i <= scc_cnt; ++i) reach[i].reset();
// 逆拓扑序:从后往前,保证子节点已经计算完
for (int idx = (int)topo.size() - 1; idx >= 0; --idx) {
int u = topo[idx];
reach[u].set(u); // 能到达自己
for (int v : comp_adj[u]) {
reach[u] |= reach[v]; // 合并子节点的可达集合
}
}
// 5. 计算每个 SCC 起点能到达的原点总数 R[u],以及最终答案
vector<long long> R(scc_cnt + 1, 0);
for (int i = 1; i <= scc_cnt; ++i) {
long long cnt = 0;
// 遍历所有 SCC j,若 reach[i][j] 为 1,则加上 scc_size[j]
for (int j = 1; j <= scc_cnt; ++j)
if (reach[i].test(j)) cnt += scc_size[j];
R[i] = cnt;
}
// 答案 = sum over SCC i: scc_size[i] * R[i]
long long ans = 0;
for (int i = 1; i <= scc_cnt; ++i) ans += 1LL * scc_size[i] * R[i];
cout << ans << "\n";
return 0;
}
精简代码
如果不做scc去重边, 并知道scc编号顺序就是拓扑逆序,代码还可以进一步精简,
忘记可参考这个文章:tarjan强联通分量和缩点
#include <bits/stdc++.h>
using namespace std;
const int N=2e3+10;
int n;
vector<int> g[N];
int dfn[N], low[N], t;
int stk[N], ins[N], top;
int scc_id[N], scc_cnt, scc_size[N];
void tarjan(int u){
dfn[u]=low[u]=++t;
stk[++top]=u; ins[u]=1;
for(auto v:g[u]){
if(!dfn[v]){
tarjan(v);
low[u]=min(low[u], low[v]);
}else if(ins[v]){
low[u]=min(low[u], dfn[v]);
}
}
if(dfn[u]==low[u]){
scc_cnt++;
while(true){
int x=stk[top--];
ins[x]=0;
scc_id[x]=scc_cnt;
scc_size[scc_cnt]++;
if(x==u) break;
}
}
}
int main()
{
cin>>n;
for(int i=1;i<=n;i++){
for(int j=1;j<=n;j++){
char x;cin>>x;
if(x=='1') g[i].push_back(j);
}
}
// 1. Tarjan缩点
for(int i=1;i<=n;i++)
if(!dfn[i]) tarjan(i);
// 2. 建DAG
vector<int> dag[N];
for(int u=1;u<=n;u++){
for(auto v:g[u]){
if(scc_id[u]!=scc_id[v]){
dag[scc_id[u]].push_back(scc_id[v]);// 正边
//dag[scc_id[v]].push_back(scc_id[u]);// 反边
}
}
}
// 3. 使用 bitset 在拓扑序的逆序上合并可达集合
bitset<N> reach[N];// reach[i] 表示以 SCC i 为起点能到达的 SCC 集合(包含 i 自身)
for(int i=1;i<=scc_cnt;i++){
reach[i][i]=1;// 自己可达自己
}
// 逆拓扑序:从后往前,保证子节点已经计算完
// scc编号即逆拓扑序
for(int i=1;i<=scc_cnt;i++){
for(auto v:dag[i]){
//reach[v]|=reach[i];
reach[i]|=reach[v];
}
}
// 4. 计算答案
long long ans=0;
for(int i=1;i<=scc_cnt;i++){
for(int j=1;j<=scc_cnt;j++)
if(reach[i][j])
ans+=1LL * scc_size[i] * scc_size[j];
}
cout<<ans<<"\n";
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号