线段树懒标记模板

线段树懒标记模板

P3373 【模板】线段树 2

题目描述

如题，已知一个数列 \(a\)，你需要进行下面三种操作：

• 将某区间每一个数乘上 \(x\)；
• 将某区间每一个数加上 \(x\)；
• 求出某区间每一个数的和。

输入格式

第一行包含三个整数 \(n,q,m\)，分别表示该数列数字的个数、操作的总个数和模数。

第二行包含 \(n\) 个用空格分隔的整数，其中第 \(i\) 个数字表示数列第 \(i\) 项的初始值 \(a_i\)。

接下来 \(q\) 行每行包含若干个整数，表示一个操作，具体如下：

操作 \(1\)： 格式：1 x y k 含义：将区间 \([x,y]\) 内每个数乘上 \(k\)。

操作 \(2\)： 格式：2 x y k 含义：将区间 \([x,y]\) 内每个数加上 \(k\)。

操作 \(3\)： 格式：3 x y 含义：输出区间 \([x,y]\) 内每个数的和对 \(m\) 取模所得的结果。

输出格式

输出包含若干行整数，即为所有操作 \(3\) 的结果。

输入输出样例 #1

输入 #1

5 5 38
1 5 4 2 3
2 1 4 1
3 2 5
1 2 4 2
2 3 5 5
3 1 4

输出 #1

17
2

说明/提示

【数据范围】

对于 \(30\%\) 的数据：\(n \le 8\)，\(q \le 10\)。
对于 \(70\%\) 的数据：$n \le 10^3 \(，\)q \le 10^4$。
对于 \(100\%\) 的数据：\(1 \le n \le 10^5\)，\(1 \le q \le 10^5,1\le a_i,k\le 10^4\)。

除样例外，\(m = 571373\)。

（数据已经过加强 ^_）

样例说明：

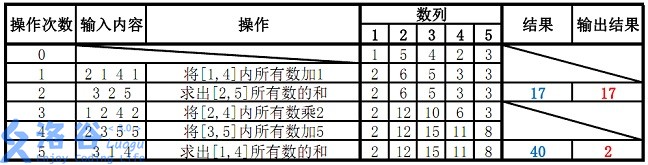
故输出应为 \(17\)、\(2\)（\(40 \bmod 38 = 2\)）。

Response:

这道题是典型的线段树 + 懒标记模板题，不过难度在于：既有「加法」的区间操作，又有「乘法」的区间操作，而且两者会互相影响。

我来一步步讲清楚思路，然后给出带详细注释的 C++ 代码。

---

一、核心思路

我们需要支持三种操作：

1. 区间乘法（所有元素都乘 \(k\) ）
2. 区间加法（所有元素都加 \(k\) ）
3. 区间求和

显然是 线段树区间操作 的场景。

1. 线段树节点信息

• sum：区间和，对 \(m\) 取模保存。

2. 懒标记

为了高效处理「区间加」「区间乘」操作，我们引入两个懒标记：

• mul：表示当前区间的所有元素需要乘的因子。
• add：表示当前区间的所有元素需要加的值。

注意：初始时，mul = 1（不改变值），add = 0。

---

3. 区间更新公式

假设我们要更新一个区间 \([l, r]\) ，长度为 len = r-l+1：

• 区间乘法（乘 \(k\) ）：
  \[\text{sum} = \text{sum} \times k \pmod m \]
  同时要修改懒标记：
  \[\text{mul} \gets \text{mul} \times k \pmod m \]
  \[\text{add} \gets \text{add} \times k \pmod m \]

• 区间加法（加 \(k\) ）：
  \[\text{sum} = \text{sum} + k \times \text{len} \pmod m \]
  懒标记更新：
  \[\text{add} \gets \text{add} + k \pmod m \]

---

4. 懒标记下传（pushdown）

当递归到子区间时，需要把父节点的懒标记分发给两个儿子。

假设当前节点的懒标记是 mul, add，传递到子区间时：

• 儿子的 sum 先整体乘 mul，再整体加 add * 子区间长度。
• 儿子的懒标记也要更新：
  • son.mul = son.mul * mul % m
  • son.add = (son.add * mul + add) % m

最后清空父节点的懒标记：mul=1, add=0。

---

二、完整代码（OI风格，详细注释）

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;

const int MAXN = 1e5 + 5;

struct Node {
    ll sum;   // 区间和
    ll mul;   // 乘法懒标记
    ll add;   // 加法懒标记
} seg[MAXN << 2];

int n, q;
ll mod;
ll a[MAXN];

#define ls (p<<1)
#define rs (p<<1|1)

// 建树
void build(int p, int l, int r) {
    seg[p].mul = 1; // 初始乘法标记为1
    seg[p].add = 0; // 初始加法标记为0
    if (l == r) {
        seg[p].sum = a[l] % mod;
        return;
    }
    int mid = (l + r) >> 1;
    build(ls, l, mid);
    build(rs, mid + 1, r);
    seg[p].sum = (seg[ls].sum + seg[rs].sum) % mod;
}

// 下传懒标记
void pushdown(int p, int l, int r) {
    int mid = (l + r) >> 1;
    int llen = mid - l + 1;   // 左子区间长度
    int rlen = r - mid;       // 右子区间长度

    // 左儿子更新
    seg[ls].sum = (seg[ls].sum * seg[p].mul % mod + seg[p].add * llen % mod) % mod;
    seg[ls].mul = seg[ls].mul * seg[p].mul % mod;
    seg[ls].add = (seg[ls].add * seg[p].mul % mod + seg[p].add) % mod;

    // 右儿子更新
    seg[rs].sum = (seg[rs].sum * seg[p].mul % mod + seg[p].add * rlen % mod) % mod;
    seg[rs].mul = seg[rs].mul * seg[p].mul % mod;
    seg[rs].add = (seg[rs].add * seg[p].mul % mod + seg[p].add) % mod;

    // 清空父节点懒标记
    seg[p].mul = 1;
    seg[p].add = 0;
}

// 区间乘法
void update_mul(int p, int l, int r, int L, int R, ll k) {
    if (L <= l && r <= R) {
        seg[p].sum = seg[p].sum * k % mod;
        seg[p].mul = seg[p].mul * k % mod;
        seg[p].add = seg[p].add * k % mod;
        return;
    }
    pushdown(p, l, r);
    int mid = (l + r) >> 1;
    if (L <= mid) update_mul(ls, l, mid, L, R, k);
    if (R > mid)  update_mul(rs, mid + 1, r, L, R, k);
    seg[p].sum = (seg[ls].sum + seg[rs].sum) % mod;
}

// 区间加法
void update_add(int p, int l, int r, int L, int R, ll k) {
    if (L <= l && r <= R) {
        seg[p].sum = (seg[p].sum + k * (r - l + 1)) % mod;
        seg[p].add = (seg[p].add + k) % mod;
        return;
    }
    pushdown(p, l, r);
    int mid = (l + r) >> 1;
    if (L <= mid) update_add(ls, l, mid, L, R, k);
    if (R > mid)  update_add(rs, mid + 1, r, L, R, k);
    seg[p].sum = (seg[ls].sum + seg[rs].sum) % mod;
}

// 区间查询
ll query(int p, int l, int r, int L, int R) {
    if (L <= l && r <= R) return seg[p].sum;
    pushdown(p, l, r);
    int mid = (l + r) >> 1;
    ll ans = 0;
    if (L <= mid) ans = (ans + query(ls, l, mid, L, R)) % mod;
    if (R > mid)  ans = (ans + query(rs, mid + 1, r, L, R)) % mod;
    return ans;
}

int main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);

    cin >> n >> q >> mod;
    for (int i = 1; i <= n; i++) cin >> a[i];

    build(1, 1, n);

    while (q--) {
        int op, x, y;
        ll k;
        cin >> op;
        if (op == 1) {
            cin >> x >> y >> k;
            update_mul(1, 1, n, x, y, k % mod);
        } else if (op == 2) {
            cin >> x >> y >> k;
            update_add(1, 1, n, x, y, k % mod);
        } else {
            cin >> x >> y;
            cout << query(1, 1, n, x, y) % mod << "\n";
        }
    }
    return 0;
}

---

三、总结

• 这题的关键是 同时维护加法和乘法懒标记，并且注意两者之间的影响。
• 懒标记的更新顺序必须清晰：
  • 「乘」操作会同时影响 mul 和 add。
  • 「加」操作只改变 add。
• 每次更新都要对模数取余，避免溢出。

这样就能在 \(O(\log n)\) 时间内完成所有操作，足以应对 \(10^5\) 的数据规模。

要不要我帮你画一个懒标记传递的流程图，直观展示「父标记」怎么影响到「子标记」？

Prompt:

懒标记的更新顺序必须清晰： * 「乘」操作会同时影响 `mul` 和 `add`。 * 「加」操作只改变 `add`。

为什么

Response:

好问题 👍
这个点正是这道题的 核心难点。我来通俗地解释为什么 乘法操作会影响 mul 和 add，而加法操作只影响 add。

---

1. 懒标记的本质

懒标记的含义是：

“如果以后需要把某个区间里的所有数更新，就按这个规则去更新。”

我们用了两个标记：

• mul：乘法因子（初始为 1，不改变值）
• add：加法因子（初始为 0，不改变值）

某个区间的真实值（设原值是 \(v\) ）会变成：

\[v \;\;\mapsto\;\; v \times \text{mul} + \text{add} \]

---

2. 思考两种操作

（1）区间乘法

假设原来的懒标记是：

\[v \mapsto v \times mul + add \]

现在我们要再「乘上 \(k\) 」，则新的值变成：

\[(v \times mul + add) \times k = v \times (mul \times k) + (add \times k) \]

结论：

• mul 要变成 mul * k
• add 要变成 add * k

所以 乘法会同时改变 mul 和 add。

---

（2）区间加法

假设原来的懒标记是：

\[v \mapsto v \times mul + add \]

现在我们要再「加上 \(k\) 」，则新的值变成：

\[(v \times mul + add) + k = v \times mul + (add + k) \]

结论：

• mul 不变
• add 变成 add + k

所以 加法只影响 add。

---

3. 小例子验证

假设某个位置的值是 \(v=5\) ，初始 mul=2, add=3，即：

\[v \mapsto v \times 2 + 3 \]

• 如果现在对区间再「乘 4」：
  \((5 \times 2 + 3) \times 4 = 52\)
  对应懒标记变化：mul=2*4=8, add=3*4=12。
• 如果现在对区间再「加 7」：
  \((5 \times 2 + 3) + 7 = 20\)
  对应懒标记变化：mul=2 不变, add=3+7=10。

和公式完全一致 ✅。

---

4. 总结

• 乘法操作会把整个「线性变换」放大，所以必须同时作用在 mul 和 add 上。
• 加法操作只是单纯在结果后面再加个数，所以只修改 add。

---