最短路相关题目

P5683 [CSP-J2019 江西] 道路拆除
https://www.luogu.com.cn/problem/P5683

错误做法

#include<bits/stdc++.h>
using namespace std;
const int N=3e3+100,M=3e3+100;
struct edge{
	int nex,to;
}e[M*2];
int h[N],top;
int n,m,t1,t2,e1,e2,st=1;
int dis[N],vis[N],pre[N],ans,used[N];
void add(int u,int v){
	e[++top]={h[u],v};
	h[u]=top;
}
void BFS(int s){
	queue<int> q;
	q.push(s);
	vis[s]=1;
	pre[s]=-1;
	while(!q.empty()){
		int x=q.front(); q.pop();
		for(int i=h[x];i;i=e[i].nex){
			int to=e[i].to;
			if(vis[to]) continue;
			dis[to]=dis[x]+1;
			pre[to]=x;
			vis[to]=1;
			q.push(to);
		}
	}
}
void dfs(int x){
	if(used[x]) {
		return;
	}
	
	used[x]=1;
	if(pre[x]==-1) return;
	ans++;
    #ifndef ONLINE_JUDGE
    cout<<x<<" ";
    #endif
	dfs(pre[x]);
}
int main(){
	cin>>n>>m;
	for(int i=1;i<=m;i++){
		int u,v;
		cin>>u>>v;
		add(u,v);
		add(v,u);
	}
	cin>>e1>>t1>>e2>>t2;
	BFS(st);
	if(dis[e1]>t1||dis[e2]>t2||(!vis[e1])||(!vis[e2])){
		cout<<-1<<endl;
		return 0;
	}
    #ifndef ONLINE_JUDGE
    cout<<"dfs(e1)\n";
    #endif
	dfs(e1);
    #ifndef ONLINE_JUDGE
    cout<<"\ndfs(e2)\n";
    #endif
	dfs(e2);
	cout<<m-ans<<endl;
    return 0;
}

该做法在bfs中记录路径。但最短路可能多条，bfs只能记录最早访问的那条（后续访问的由于vis标记，不会进去）
这就导致了问题，比如下面这个测试用例
input:

5 5
1 2
2 5
2 3
3 4
4 5
5 3 4 3

output:

2

该错误算法会输出1。原因是dfs回溯时候走了2个不同的路径（有运气因数，有可能不会走不同路径，这要看bfs时候的遍历顺序），导致路径复用数变少。如下图

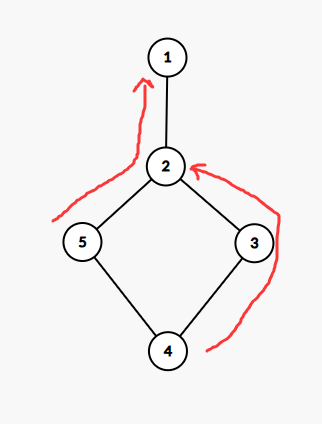
所以正确的做法是：

#include <bits/stdc++.h>
using namespace std;
const int N=3e3+10, M=N;
struct edge{
	int nxt, to;
}e[M*2]; 
int h[N], cnt;
void add(int u, int v)
{
	e[++cnt]={h[u], v};
	h[u]=cnt;
}
int n, m, x, y, s1, t1, s2, t2;
int d[N], d1[N], d2[N];
bool vis[N];
void bfs(int s, int d[]){
	queue<int> q;
	q.push(s);
	memset(vis, 0, sizeof vis);
    memset(d, 0x3f, sizeof d);
	vis[s]=1;
	d[s]=0;
	while(!q.empty()){
		int u=q.front(); q.pop();
		for(int i=h[u]; i; i=e[i].nxt){
			int to=e[i].to;
			if(!vis[to]){
				vis[to]=1;
				d[to]=d[u]+1;
				q.push(to);
			}
		}
	}
}
int main(){
	cin>>n>>m;
	for(int i=1;i<=m;i++){
		cin>>x>>y;
		add(x, y); add(y,x);
	}
	cin>>s1>>t1>>s2>>t2;
	bfs(1, d);
	if(d[s1]>t1||d[s2]>t2) {
		cout<<-1; return 0;
	}
//	cout<<d[s1]<<endl<<d[s2]<<endl;
	bfs(s1, d1);
	bfs(s2, d2);
	
	int ans=INT_MAX;
	for(int i=1;i<=n;i++)
		if(d[i]+d1[i]==d[s1]&&d[i]+d2[i]==d[s2])
            ans=min(ans, d[i]+d1[i]+d2[i]);				
	cout<<m-ans;
	return 0;
} 

升级版：
CF543B Destroying Roads
https://www.luogu.com.cn/problem/CF543B

正难则反。 要求摧毁最多，就是要保留最少。如果是一对顶点，保留最少其实就是求最短路径。 m-最短路径长度就是答案。

回到原问题。

1、路径不交叉。以这种方式，我们可以用以下值更新答案：m - d[s 0 ][t 0 ] - d[s 1 ][t 1 ]（只要路径长度的条件满足）

2、否则路径交叉，正确的答案看起来像字母'H'。更正式地说，开始时两条路径将包含不同的边，之后路径将包含相同的边，并以不同的边结束。让我们迭代对(i, j)—路径相同部分的起始和结束顶点。然后我们可以用以下值更新答案：m - d[s 0 ][i] - d[i][j] - d[j][t 0 ] - d[s 1 ][i] - d[j][t 1 ]（只要路径长度的条件满足）。

请注意，我们需要交换顶点 s 0 和 t 0 ，并重新检查第二种情况，因为在某些情况下将顶点 t 0 与顶点 i 连接，将顶点 s 0 与顶点 j 连接更好。

本题可以理解为：求一张图上的两条受限的最短路，答案为所有边的个数m减去两条最短路的长度和。因为两条最短路有可能存在重叠部分，所以要枚举选出最多的重叠部分，从而保证最短路长度最短。重要的是要求任意两点的最短路，结合本题数据范围\(3000\)，不适合使用\(Floyd(O(n^3))\)算法，观察到边权都为1，因此可以使用bfs求最短路。

#include<bits/stdc++.h>
using namespace std;
#define maxn 3010
int n,m,s1,t1,l1,s2,t2,l2;
int head[maxn],num;
struct node{
	int to,nxt;
}es[maxn<<1];

void insert_edge(int u,int v){//建图-无向图
	es[++num].to=v;
	es[num].nxt=head[u];
	head[u]=num;
}

int dis[maxn][maxn];
bool vis[maxn<<1];
queue<int>q;
void bfs(){//bfs求最短路 
	memset(dis,0x3f,sizeof dis);
	for(int i=1;i<=n;i++){
		memset(vis,false,sizeof vis);
		q.push(i);
		dis[i][i]=0;
		vis[i]=true; 
		while(!q.empty()){
			int u=q.front();
			q.pop();
			for(int j=head[u];j;j=es[j].nxt){
				int v=es[j].to;
				if(!vis[v]){
					dis[i][v]=dis[i][u]+1; 
					q.push(v);
					vis[v]=true;
				}
			}
		}
	}
}

int main(){
	ios::sync_with_stdio(false);
	cin.tie(0);cout.tie(0);
	cin>>n>>m;
	for(int i=1;i<=m;i++){
		int u,v;
		cin>>u>>v;
		insert_edge(u,v);
		insert_edge(v,u);
	}
	bfs();
	cin>>s1>>t1>>l1>>s2>>t2>>l2;
	if(dis[s1][t1]>l1 || dis[s2][t2]>l2){
		cout<<-1;
		return 0;
	}
	int dist1,dist2,ans=min(m,dis[s1][t1]+dis[s2][t2]);
	for(int i=1;i<=n;i++){
		for(int j=1;j<=n;j++){//处理两条最短路的重复边-枚举任意两点之间的最短路作为重边 
			dist1=dis[i][j]+dis[i][s1]+dis[j][t1];
			dist2=dis[i][j]+dis[i][s2]+dis[j][t2];
			if(dist1<=l1 && dist2<=l2)
				ans=min(ans,dist1+dist2-dis[i][j]);
				
			dist1=dis[i][j]+dis[i][s1]+dis[j][t1];//重边有可能是相反的路径 
			dist2=dis[i][j]+dis[i][t2]+dis[j][s2];
			if(dist1<=l1 && dist2<=l2)
				ans=min(ans,dist1+dist2-dis[i][j]);
		}
	} 
	cout<<m-ans<<endl;
	return 0;
}