F - Sorting a Matrix 矩阵定序

但如果对每一行暴力连边，一行内的边数最多是C(m,2)的，总数n*C(m,2)，不能接受

假设有两列的值是1，两列的值是2，考虑按如下图示，优化建边数

优化后，总的点数大致在2e6级别，而边数也大致在4e6级别，直接topo排序即可

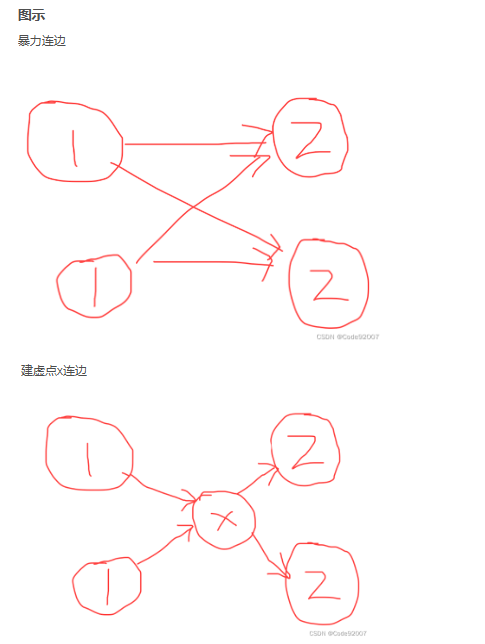
虚点的做法
之前只是在最短路中搞过虚点，实际这题说明，
需要连n*m条边的场合，都可以考虑尝试是不是能优化成n+m条边的

#include <bits/stdc++.h>
using namespace std;

int main() {
    ios::sync_with_stdio(0); cin.tie(0);
    int H, W;
    cin >> H >> W;
    vector<int> A(H * W);
    for (int i = 0; i < H * W; i++)
        cin >> A[i];

    // 1. 行排序：计算每行非零元素的 [min, max] 区间，检查区间是否两两不交叉
    vector<pair<int,int>> rows;
    rows.reserve(H);
    for (int i = 0; i < H; i++) {
        int mn = INT_MAX, mx = INT_MIN;
        for (int j = 0; j < W; j++) {
            int v = A[i * W + j];
            if (v > 0) {
                mn = min(mn, v);
                mx = max(mx, v);
            }
        }
        if (mn <= mx) rows.emplace_back(mn, mx);
    }
    sort(rows.begin(), rows.end());
    for (int i = 1; i < (int)rows.size(); i++) {
        // 若前一行的最大值 > 下一行的最小值，则无解
        if (rows[i-1].second > rows[i].first) {
            cout << "No\n";
            return 0;
        }
    }

    // 2. 列依赖图：节点 1..W 为原列，后面节点为动态分配的“虚拟节点”
    int nextId = W;                              // 下一个可用节点编号
    int maxNodes = W + H * W + 5;                // 保证足够空间
    vector<vector<int>> G(maxNodes);
    vector<int> indeg(maxNodes, 0);

    // 对每一行构造依赖
    for (int i = 0; i < H; i++) {
        // 收集本行的 (value, col)
        vector<pair<int,int>> v;
        v.reserve(W);
        for (int j = 0; j < W; j++) {
            int x = A[i * W + j];
            if (x > 0) v.emplace_back(x, j+1);
        }
        if (v.empty()) continue;
        sort(v.begin(), v.end());  // 按值升序

        // 在相邻不同值之间插入虚拟节点，连接块间依赖
        for (int k = 1; k < (int)v.size(); k++) {
            if (v[k-1].first != v[k].first) {
                int smallVal = v[k-1].first;
                int vnode = ++nextId;  // 分配新虚拟节点

                // 小值块所有列 -> vnode
                for (int t = k-1; t >= 0 && v[t].first == smallVal; t--) {
                    G[v[t].second].push_back(vnode);
                }
                // vnode -> 大值块所有列
                int largeVal = v[k].first;
                for (int t = k; t < (int)v.size() && v[t].first == largeVal; t++) {
                    G[vnode].push_back(v[t].second);
                }
            }
        }
    }

    // 3. 构造入度并检测环（Kahn 算法）
    int N = nextId;
    for (int u = 1; u <= N; u++) {
        for (int v : G[u]) {
            indeg[v]++;
        }
    }

    queue<int> q;
    for (int u = 1; u <= N; u++) {
        if (indeg[u] == 0) q.push(u);
    }

    int seen = 0;
    while (!q.empty()) {
        int u = q.front(); q.pop();
        seen++;
        for (int v : G[u]) {
            if (--indeg[v] == 0) {
                q.push(v);
            }
        }
    }

    // 如果能访问 N 个节点，无环；否则有环
    cout << (seen == N ? "Yes\n" : "No\n");
    return 0;
}