P2680 [NOIP 2015 提高组] 运输计划

题目背景

NOIP2015 Day2T3

题目描述

公元 \(2044\) 年，人类进入了宇宙纪元。

L 国有 \(n\) 个星球，还有 \(n-1\) 条双向航道，每条航道建立在两个星球之间，这 \(n-1\) 条航道连通了 L 国的所有星球。

小 P 掌管一家物流公司，该公司有很多个运输计划，每个运输计划形如：有一艘物流飞船需要从 \(u_i\) 号星球沿最快的宇航路径飞行到 \(v_i\) 号星球去。显然，飞船驶过一条航道是需要时间的，对于航道 \(j\)，任意飞船驶过它所花费的时间为 \(t_j\)，并且任意两艘飞船之间不会产生任何干扰。

为了鼓励科技创新， L 国国王同意小 P 的物流公司参与 L 国的航道建设，即允许小 P 把某一条航道改造成虫洞，飞船驶过虫洞不消耗时间。

在虫洞的建设完成前小 P 的物流公司就预接了 \(m\) 个运输计划。在虫洞建设完成后，这 \(m\) 个运输计划会同时开始，所有飞船一起出发。当这 \(m\) 个运输计划都完成时，小 P 的物流公司的阶段性工作就完成了。

如果小 P 可以自由选择将哪一条航道改造成虫洞，试求出小 P 的物流公司完成阶段性工作所需要的最短时间是多少？

输入格式

第一行包括两个正整数 \(n, m\)，表示 L 国中星球的数量及小 P 公司预接的运输计划的数量，星球从 \(1\) 到 \(n\) 编号。

接下来 \(n-1\) 行描述航道的建设情况，其中第 \(i\) 行包含三个整数 \(a_i, b_i\) 和 \(t_i\)，表示第 \(i\) 条双向航道修建在 \(a_i\) 与 \(b_i\) 两个星球之间，任意飞船驶过它所花费的时间为 \(t_i\)。

接下来 \(m\) 行描述运输计划的情况，其中第 \(j\) 行包含两个正整数 \(u_j\) 和 \(v_j\)，表示第 \(j\) 个运输计划是从 \(u_j\) 号星球飞往 \(v_j\)号星球。

输出格式

一个整数，表示小 P 的物流公司完成阶段性工作所需要的最短时间。

输入输出样例 #1

输入 #1

6 3
1 2 3
1 6 4
3 1 7
4 3 6
3 5 5
3 6
2 5
4 5

输出 #1

说明/提示

所有测试数据的范围和特点如下表所示

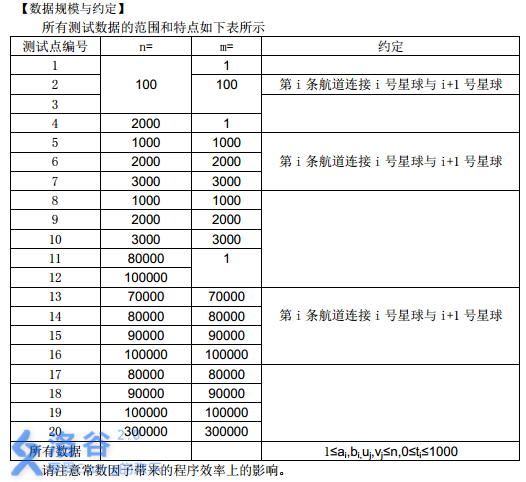
请注意常数因子带来的程序效率上的影响。

对于 \(100\%\) 的数据，保证：\(1 \leq a_i,b_i \leq n\)，\(0 \leq t_i \leq 1000\)，\(1 \leq u_i,v_i \leq n\)。思路：

Response:

二分，倍增与树上差分。

考虑二分答案，设所有运输计划的时间的最大的最小值为 k，判断是否能够改一条边权值为 0 使得所有运输路径的权值小于等于 k。

首先可以将运输计划分类：

路径权值小于 k；
路径权值大于 k。
改造的边一定是在第二类运输计划的路径的公共边上，否则不可能使所有运输路径的权值小于等于 k，因为这一条边不在其中一个第二类运输计划的路径上，那么这一个运输计划就不会改变路径权值之和。

接下来考虑如何选择边。用一个数组记录 x 与它父节点组成的边被覆盖的次数，当然不能直接算，这里用差分优化。最终被覆盖的总次数为第二种运输计划的数量就是可以选择修改的边。

求出所有可以修改的边的最大权值，再判断最大的运输路径的权值和减去可以修改的边的最大权值是否小于等于 k。

最后，求路径权值和肯定不能暴力，可以用一个数组记录从根节点到当前节点的权值和，再预处理一个倍增表，就可以比较快速求出两点之间的路径权值和。

一、算法思路

问题等价
我们要在一棵有权重的树上，给定 \(m\) 条路径，每条路径的“执行时间”是该路径上所有边权之和。可以把任意一条边改造成“虫洞”（权重变为 0），希望在最坏（最长）一条运输路径的时间最少。
二分答案
设答案为 \(T\) 。若对于某个 \(T\) ，能够通过改造一条边，使得每条路径的时间都 \(\le T\) ，则称该 \(T\) 是可行的。目标是找到最小的可行 \(T\) ，可对 \(T\) 做二分搜索。
预处理：深度、父节点、到根的距离与倍增 LCA
- 任取节点 1 作为根，DFS 预处理每个节点的深度 deep[u]、父节点 fa[u][0]，以及从根到该节点的距离 dist[u]（边权和）。
- 构建倍增表 fa[u][k]，用来 \(O(\log n)\) 求两点 LCA。
对于给定 \(T\) 的可行性检查（check(T)）
- 先遍历所有 \(m\) 条路径，计算其原始长度 \(d_i\) 。若 \(d_i \le T\) ，此路径无需调整；否则称其为“要压缩”的路径。
- 只有落在所有“要压缩”路径的公共边上的那条边，才能同时影响这些路径的长度。于是我们要统计每条边被多少个“要压缩”路径所经过。
- 用树上差分技巧：对每条要压缩路径的端点 \(u\) 与 \(v\) ，在 cnt[u]++，cnt[v]++，cnt[LCA] -= 2；DFS 回退汇总后，若一条边连接子节点 \(x\) 与其父 \(p\) ，则 cnt[x] 就是这条边被多少路径覆盖。
- 记“要压缩”的路径中最大原始长度为 \(\max d_i\) 。若存在一条被所有这类路径覆盖的边，其重量为 \(w\) ，则将这条边改虫洞后，最长路径的新长度为 \(\max d_i - w\) 。只要满足
  
  \[ \max d_i - w \;\le\; T \]
  即可。
整体复杂度
- 建树与一次 DFS： \(O(n)\) 。
- 倍增表预处理： \(O(n\log n)\) 。
- 二分答案区间在 \([0,\max d_i]\) ，每次可行性检查需要一次对 \(m\) 条路径的遍历和一遍差分 DFS，复杂度 \(O\bigl((n+m)\bigr)\) 。
- 总体： \(O\bigl((n+m)\log(\max d_i) + n\log n\bigr)\) ，满足 \(n,m\le3\times10^5\) 。

二、C++ 代码实现

#include <bits/stdc++.h>
using namespace std;
using ll = long long;

// 最大节点数和路径数
const int MAXN = 300000 + 5;

// 邻接表存图
struct Edge { int to, w; };
vector<Edge> G[MAXN];

// LCA 二倍增、深度、从根到节点距离
int fa[MAXN][20], lg2[MAXN], depth[MAXN];
ll distRoot[MAXN];

// 差分计数数组
int cnt[MAXN];

// 运输计划
int U[MAXN], V[MAXN], LCAij[MAXN];
ll pathLen[MAXN];

int n, m;

// 第一次 DFS：求 depth[], fa[][0], distRoot[]
void dfs1(int u, int p) {
    fa[u][0] = p;
    depth[u] = depth[p] + 1;
    for (auto &e : G[u]) {
        int v = e.to;
        if (v == p) continue;
        distRoot[v] = distRoot[u] + e.w;
        dfs1(v, u);
    }
}

// 计算 LCA（O(log n)）
int lca(int x, int y) {
    if (depth[x] < depth[y]) swap(x, y);
    // 抬 x 到同深度
    int d = depth[x] - depth[y];
    for (int k = 0; k <= lg2[d]; ++k)
        if (d >> k & 1) x = fa[x][k];
    if (x == y) return x;
    // 同时向上抬
    for (int k = lg2[depth[x]]; k >= 0; --k) {
        if (fa[x][k] != fa[y][k]) {
            x = fa[x][k];
            y = fa[y][k];
        }
    }
    return fa[x][0];
}

// 第二次 DFS：汇总差分，cnt[x] 累加其子树
void dfs2(int u, int p) {
    for (auto &e : G[u]) {
        int v = e.to;
        if (v == p) continue;
        dfs2(v, u);
        cnt[u] += cnt[v];
    }
}

// 检查给定 T 是否可行
bool check(ll T) {
    // 清零
    fill(cnt, cnt + n + 1, 0);

    int need = 0;      // 要压缩的路径数量
    ll maxLen = 0;     // 这些路径中最大原始长度

    // 标记差分
    for (int i = 1; i <= m; ++i) {
        if (pathLen[i] > T) {
            ++need;
            int a = U[i], b = V[i], c = LCAij[i];
            cnt[a]++; cnt[b]++; cnt[c] -= 2;
            maxLen = max(maxLen, pathLen[i]);
        }
    }
    if (need == 0) return true;  // 全部路径已 ≤ T

    // 汇总差分到 cnt[]
    dfs2(1, 0);

    // 寻找被所有路径覆盖的边
    for (int v = 2; v <= n; ++v) {
        // 边 (fa[v][0], v) 被 cnt[v] 条路径覆盖
        if (cnt[v] == need) {
            ll w = distRoot[v] - distRoot[fa[v][0]];  // 边权
            // 如果去掉这条边，最长压缩后 ≤ T
            if (maxLen - w <= T) return true;
        }
    }
    return false;
}

int main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);

    // 读入
    cin >> n >> m;
    for (int i = 1; i < n; ++i) {
        int a, b, w;
        cin >> a >> b >> w;
        G[a].push_back({b, w});
        G[b].push_back({a, w});
    }

    // 预处理 lg2[]
    lg2[1] = 0;
    for (int i = 2; i <= n; ++i)
        lg2[i] = lg2[i >> 1] + 1;

    // DFS1 建立 depth[], fa[][0], distRoot[]
    dfs1(1, 0);

    // 倍增表 fa[][k]
    for (int k = 1; k <= lg2[n]; ++k) {
        for (int u = 1; u <= n; ++u) {
            fa[u][k] = fa[ fa[u][k-1] ][k-1];
        }
    }

    // 读路径，求 LCA 及长度
    ll lo = 0, hi = 0;
    for (int i = 1; i <= m; ++i) {
        cin >> U[i] >> V[i];
        int c = lca(U[i], V[i]);
        LCAij[i] = c;
        pathLen[i] = distRoot[U[i]] + distRoot[V[i]] - 2 * distRoot[c];
        hi = max(hi, pathLen[i]);
    }

    // 二分答案区间 [0, hi]
    ll ans = hi, L = 0, R = hi;
    while (L <= R) {
        ll mid = (L + R) >> 1;
        if (check(mid)) {
            ans = mid;
            R = mid - 1;
        } else {
            L = mid + 1;
        }
    }

    cout << ans << "\n";
    return 0;
}

代码要点说明：

使用两次 DFS，一次预处理深度和父节点，第二次汇总差分。
差分技巧可以在 \(O(n)\) 内统计每条边覆盖的路径数量。
二分答案并在每次检查时遍历所有路径与一次 DFS，总体复杂度符合要求。

这样就能求出将哪条边改造成虫洞后，所有运输计划完成所需的最短时间。

posted @ 2025-05-22 16:15 katago 阅读(52) 评论(0) 收藏举报

刷新页面返回顶部

Just run

P2680 [NOIP 2015 提高组] 运输计划

P2680 [NOIP 2015 提高组] 运输计划

题目背景

题目描述

输入格式

输出格式

输入输出样例 #1

输入 #1

输出 #1

说明/提示

Response:

一、算法思路

二、C++ 代码实现

公告