树形动态规划
树形动态规划实现
在树形结构中,我们可以利用树形动态规划(Tree DP)高效地在 \(O(n)\) 时间内计算每个节点的一些信息,比如:
-
每个节点子树中节点的数量(包括它自己);
-
从每个节点出发,到达叶子节点的最长路径长度(也叫深度);
一、问题背景
我们处理的是一棵 有根树(Rooted Tree),也就是我们指定了一个根节点(比如 1 号节点),然后我们要从这个根开始向下递归处理。如果是无根树,随便选一个点作为根。
我们采用 DFS(深度优先搜索)+ 记忆/递推的方式来做,也就是所谓的树形 DP。
🌲 子树大小计算
思路说明
- 每个节点的子树大小 = 所有子节点的子树大小之和 + 1(加上自己)
C++ 代码(树的子节点用邻接表存)
#include <iostream>
#include <vector>
using namespace std;
const int N = 1e5 + 10; // 最大节点数,根据题目调整
vector<int> tree[N]; // 邻接表表示树
int sz[N]; // sz[u] 表示 u 的子树大小(包括 u 自己)
// dfs 函数,当前节点是 u,父亲是 fa
void dfs(int u, int fa) {
sz[u] = 1; // 自己先算一个
for (int v : tree[u]) {
if (v == fa) continue; // 避免走回父亲
dfs(v, u); // 递归处理子节点
sz[u] += sz[v]; // 把子节点的子树大小加进来
}
}
int main() {
int n; cin >> n;
for (int i = 1; i < n; i++) {
int u, v; cin >> u >> v;
tree[u].push_back(v);
tree[v].push_back(u); // 无向边
}
dfs(1, 0); // 从根节点 1 开始,父亲设为 0 表示无
for (int i = 1; i <= n; i++) {
cout << "节点 " << i << " 的子树大小为: " << sz[i] << endl;
}
return 0;
}
🌿 从每个节点出发的最长路径(深度)
思路说明
- 每个节点的深度 = 它的所有子节点的深度的最大值 + 1
C++ 代码
#include <iostream>
#include <vector>
using namespace std;
const int N = 1e5 + 10;
vector<int> tree[N];
int depth[N]; // depth[u] 表示从 u 到叶子最长路径长度
void dfs(int u, int fa) {
depth[u] = 0; // 先设为0,如果没有子节点就是叶子
for (int v : tree[u]) {
if (v == fa) continue;
dfs(v, u);
depth[u] = max(depth[u], depth[v] + 1); // 选最长的子路径
}
}
int main() {
int n; cin >> n;
for (int i = 1; i < n; i++) {
int u, v; cin >> u >> v;
tree[u].push_back(v);
tree[v].push_back(u);
}
dfs(1, 0); // 从根节点 1 开始
for (int i = 1; i <= n; i++) {
cout << "从节点 " << i << " 出发到叶子的最长路径长度为: " << depth[i] << endl;
}
return 0;
}
✅ 总结
这些都是典型的**“子问题合并到父问题”的自底向上 DP”**,树形 DP 的核心就是:
-
从叶子往上处理;
-
子节点的信息合并到父节点;
-
**每条边只走一遍,时间复杂度为 \(O(n)\) **。
树形DP求树的直径:
首先,先证明一些结论:
树上任意两节点之间最长的简单路径即为树的「直径」
因为树上两点直接简单路径只有一条,这个问题就转为 两点之间距离。
又因为要求最长的简单路径,那么直径肯定就是两个叶子节点的路径。因为如果两点不是叶子节点,那么肯定可以往叶子扩展,就会更长。
两个叶子节点路径 => LCA ??
或者反过来考虑,从LCA这个根节点,计算它到两个不同的叶子的路径长度之和的最大值。
利用上面的知识,就能得到如下代码:
#include <bits/stdc++.h>
using namespace std;
const int N=1e5+5;
vector<int> g[N];
int n;
int ans=0;
int dp[N];// dp[i]表示以i为根的子树从i到叶子节点的最长路径
// dp求树的直径
void dfs(int u, int fa){
int max1=0,max2=0;// 存当前节点 u 的前两大的子树深度
for(auto v:g[u]){
if(v==fa) continue; // 避免走回父节点
dfs(v,u);
int t=dp[v]+1;// 子树的深度 + 当前边(边权为1)
if(t>max1){
max2=max1;
max1=t;
}
else if(t>max2){
max2=t;
}
}
dp[u] = max1; // 当前点向下的最大深度
ans = max(ans, max1 + max2); // 更新树的直径(两个最长子树路径相加)
}
int main()
{
cin>>n;
for(int i=1;i<n;i++)
{
int u,v;
cin>>u>>v;
g[u].push_back(v);
g[v].push_back(u);
}
dfs(1,0);
cout<<ans<<endl;
return 0;
}
#include <bits/stdc++.h>
using namespace std;
const int N = 1e5 + 5;
vector<int> g[N];
int n;
int ans = 0;
int dp[N]; // dp[i] 表示以 i 为根的子树,从 i 出发能到达的最深叶子节点的最大长度
// 一次 DFS 计算 dp[u],并在过程中更新全局直径 ans
void dfs(int u, int fa) {
dp[u] = 0; // 初始化:尚未处理任何子节点
for (auto v : g[u]) { // 遍历 u 的每个邻居 v
if (v == fa) continue; // 避免回到父节点
dfs(v, u); // 递归处理子树
// —— 更新直径 ans ——
// dp[u](此时是所有已处理子节点中的最大深度)
// + dp[v] + 1(v 子树的深度加上 u-v 这条边)
ans = max(ans, dp[u] + dp[v] + 1);
// —— 更新 dp[u] ——
// 若 v 子树加 1(边长)能够构成更深的路径,就更新 dp[u]
dp[u] = max(dp[u], dp[v] + 1);
}
}
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
cin >> n;
for (int i = 1; i < n; i++) {
int u, v;
cin >> u >> v;
g[u].push_back(v);
g[v].push_back(u);
}
dfs(1, 0);
cout << ans << "\n";
return 0;
}
这里的 dp[u] 是「在之前已经处理过的子树中,能得到的最大深度」,dp[v] + 1 是「当前子树 v 提供的深度加上 u→v 的这条边」。
两条最长向下路径加起来,正好对应「某一条经过 u 的最长路径」——我们在遍历每个子节点时,都在尝试把一条新路径和已知的最大路径配对。
最后,再更新 dp[u]
好好想想,为什么这个更新需要放在最后。
输出直径
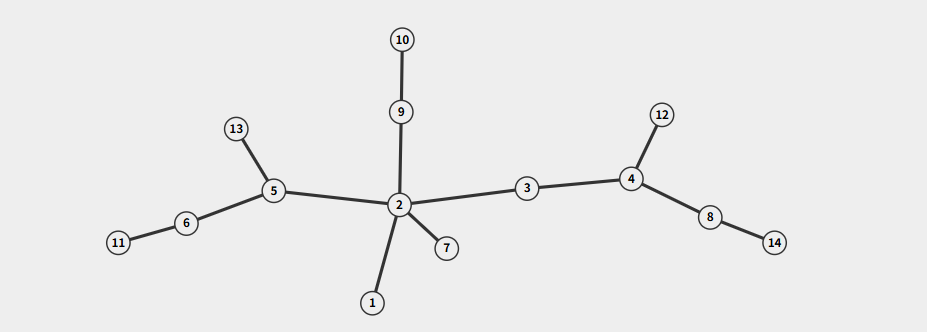
15
1 2
2 3
2 5
2 7
2 9
3 4
4 8
4 12
5 6
5 13
6 11
8 14
9 10
参考oiwiki, 则可以在 DP 的过程中,记录下每个节点能向下延伸的最长路径与次长路径(定义同上)所对应的子节点,在求
d(直径) 的同时记下对应的节点 u
参考代码如下:
#include <bits/stdc++.h>
using namespace std;
const int N=1e5+5;
vector<int> g[N];
int n;
int ans=0;
int dp[N];// dp[i]表示以i为根的子树从i到叶子节点的最长路径
// dp求树的直径
int son1[N], son2[N], father;
void dfs(int u, int fa){
int max1=0,max2=0;
for(auto v:g[u]){
if(v==fa) continue;
dfs(v,u);
int t=dp[v]+1;
if(t>max1){
max2=max1;
max1=t;
son2[u]=son1[u];//记录次长路径的儿子
son1[u]=v;//记录最长路径的儿子
}
else if(t>max2){
max2=t;
son2[u]=v;//记录次长路径的儿子
}
}
dp[u]=max1;
if(max1+max2>ans)
{
ans=max1+max2;
father=u;//记录最长路径中点
}
}
//打印直径
void print_diameter(){
int s1=son1[father], s2=son2[father];
cout<<"father: "<< father<<" ";
cout<<"son1: ";
while(s1)
{
cout<<s1<<" ";
s1=son1[s1];
}
cout<<"son2: ";
while(s2)
{
cout<<s2<<" ";
s2=son1[s2];
}
}
int main()
{
cin>>n;
for(int i=1;i<n;i++)
{
int u,v;
cin>>u>>v;
g[u].push_back(v);
g[v].push_back(u);
}
dfs(1,0);
cout<<ans<<endl;
print_diameter();
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号