P3916 图的遍历

https://www.luogu.com.cn/problem/P3916

在有向图中，找出每个点所能到达的最大编号的点。

方法一：反向图 + 从大到小 DFS/BFS

• 原图中的“能到”关系，在反向图中就变成了“能被到达”。

• 从编号最大的点开始，标记它能通过反向边走到的所有点 ⇒ 这些点最大可达编号就是它。

• 然后往下处理编号更小的点，跳过已经被更大编号覆盖的。

优点：

• 代码简单，不需要强连通分量；

• 时间复杂度 \(O(N+M)\)，适合大数据。

C++ 实现

#include <bits/stdc++.h>
using namespace std;

int main(){
    ios::sync_with_stdio(false);
    cin.tie(nullptr);

    int N, M;
    cin >> N >> M;
    vector<vector<int>> rG(N+1);
    for(int i = 0; i < M; i++){
        int u, v;
        cin >> u >> v;
        // 原图 u->v，反向图加 v->u
        rG[v].push_back(u);
    }

    vector<int> A(N+1, 0);
    queue<int> q;

    // 从大到小枚举作为 BFS 根
    for(int i = N; i >= 1; i--){
        if(A[i] != 0) continue;      // 已被更大编号的 BFS 标记过，跳过
        A[i] = i;
        q.push(i);
        while(!q.empty()){
            int u = q.front(); q.pop();
            for(int v : rG[u]){
                if(A[v] == 0){
                    A[v] = i;
                    q.push(v);
                }
            }
        }
    }

    // 输出 A[1..N]
    for(int v = 1; v <= N; v++){
        cout << A[v] << (v==N?'\n':' ');
    }
    return 0;
}

---

为什么它是线性的、且正确？

• 线性复杂度：

  • 每条反向边最多被遍历一次（当它的头节点首次被标记并入队时）；

  • 每个节点也只会被标记、入队一次。
    因此总的时间是 \(O(N+M)\)，和 SCC + 拓扑 DP 一样。

• 正确性直观：

  • 我们先处理最大的根 i=N，把所有能反向到达 N 的节点都标记为 N。

  • 再处理 i=N-1，跳过已经标记过的，剩下所有还没被更大编号覆盖的，恰好就是那些从 i 出发无法到达任何更大节点，所以它们的最大可达编号就是 i。

  • 依次类推，一次 BFS 就填好了所有节点的答案。

方法二：SCC + DAG + 拓扑 DP

思路概览

1. 求 SCC
   利用 Tarjan 算法，把原图分解成若干个强连通分量。

   • 在同一个 SCC 中，任意两点互相可达，因此它们的 \(A(v)\) 值都是相同的。

   • 对每个 SCC，记录其中点编号的最大值，记为 scc_val[i]。

2. 构造 SCC DAG

3. 在 DAG 上 DP
   记 dp[i] 为从分量 \(i\) 出发，能到达的节点编号最大值。

   • 初始化 dp[i]=scc_val[i]。

   • 对 DAG 做拓扑排序，得到序列 topo[]。

   • 逆序遍历 topo：对于每个节点 \(u\)，枚举它的每条出边 \(v\)，更新

     \[ dp[u]=\max(dp[u],\;dp[v])\;. \]

   • 这样就能把“后面可达的最大编号”向前传递回去。

4. 输出
   对于原图中的每个顶点 \(v\)，答案就是 dp[ scc[v] ]。

#include <bits/stdc++.h>
using namespace std;
using ll = long long;

const int MAXN = 100000;

int N, M;
vector<int> G[MAXN+1];

// ---- Tarjan 算法求 SCC ----
int dfn[MAXN+1], low[MAXN+1], dfs_clock = 0;
bool in_stack[MAXN+1];
stack<int> stk;
int scc[MAXN+1], scc_cnt = 0;
int scc_val[MAXN+1];  // scc_val[i] = 第 i 号分量内的最大顶点编号

void tarjan(int u) {
    dfn[u] = low[u] = ++dfs_clock;
    stk.push(u);
    in_stack[u] = true;
    for (int v : G[u]) {
        if (!dfn[v]) {
            tarjan(v);
            low[u] = min(low[u], low[v]);
        } else if (in_stack[v]) {
            low[u] = min(low[u], dfn[v]);
        }
    }
    // 发现一个 SCC
    if (low[u] == dfn[u]) {
        ++scc_cnt;
        while (true) {
            int x = stk.top(); stk.pop();
            in_stack[x] = false;
            scc[x] = scc_cnt;
            scc_val[scc_cnt] = max(scc_val[scc_cnt], x);
            if (x == u) break;
        }
    }
}

int main(){
    ios::sync_with_stdio(false);
    cin.tie(nullptr);

    cin >> N >> M;
    for (int i = 0; i < M; i++) {
        int u, v;
        cin >> u >> v;
        G[u].push_back(v);
    }

    // 1. 找 SCC
    for (int i = 1; i <= N; i++) {
        if (!dfn[i]) {
            tarjan(i);
        }
    }
    // 2. 构造 SCC DAG
    vector<vector<int>> dag(scc_cnt + 1);
    for (int u = 1; u <= N; u++) {
        for (int v : G[u]) {
            int cu = scc[u], cv = scc[v];
            if (cu != cv) {
                dag[cu].push_back(cv);
            }
        }
    }
    // 3. 拓扑排序 ，这里省略了，应为scc编号就是拓扑排序的逆序
    // 4. DAG 上逆序 DP
    vector<int> dp(scc_cnt+1, 0);
    for(int i=1;i<=scc_cnt;i++){
        dp[i]=scc_val[i];
    }

    for(int i=1;i<=scc_cnt;i++){
        for(int j:dag[i])
        {
            dp[i]=max(dp[j], dp[i]);
        }
    }
    
    // 5. 输出答案
    // 对每个原节点 v，输出 dp[ scc[v] ]
    for (int v = 1; v <= N; v++) {
        cout << dp[ scc[v] ] << (v == N ? '\n' : ' ');
    }

    return 0;
}

补充个测试用例：
input

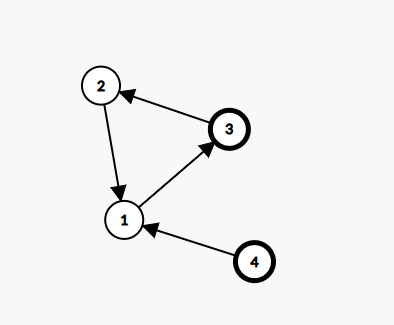
4 4
3 2
4 1
1 3
2 1

output

3 3 3 4