哈夫曼树与哈夫曼编码
哈夫曼树
哈夫曼树又称最优二叉树,是带权路径长度最短的树,可用来构造最优编码,用于信息传输、数据压缩等方面,是一种应用广泛的二叉树。 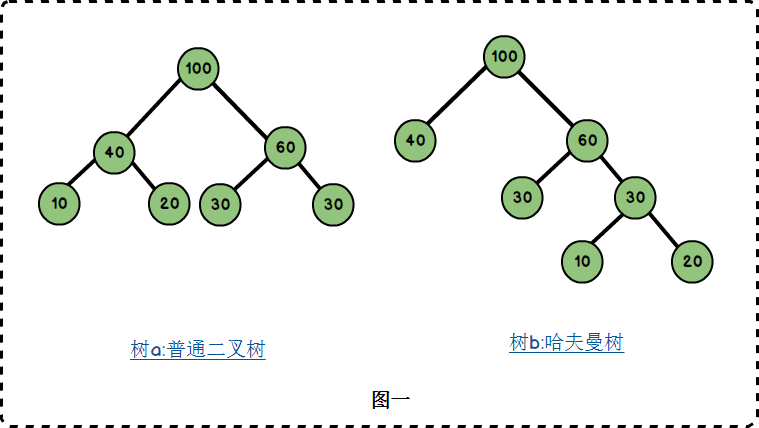
几个相关的基本概念:
1.路径:从树中一个结点到另一个结点之间的分支序列构成两个节点间的路径
2.路径长度:路径上的分支的条数称为路径长度
3.树的路径长度:从树根到每个结点的路径长度之和称为树的路径长度
4.结点的权:给树中结点赋予一个数值,该数值称为结点的权
5.带权路径长度:结点到树根间的路径长度与结点的权的乘积,称为该结点的带权路径长度
6.树的带权路径长度:树中所有叶子结点的带权路径长度之和,通常记为WPL
7.最优二叉树:在叶子个数n以及各叶子的权值确定的条件下,树的带权路径长度WPL值最下的二叉树称为最优二叉树。
哈夫曼树的建立
由哈夫曼最早给出的建立最优二叉树的带有一般规律的算法,俗称哈夫曼算法。描述如下:
1):初始化:根据给定的n个权值(W1,W2,…,Wn),构造n棵二叉树的森林集合F={T1,T2,…,Tn},其中每棵二叉树Ti只有一个权值为Wi的根节点,左右子树均为空。
2):找最小树并构造新树:在森林集合F中选取两棵根的权值最小的树做为左右子树构造一棵新的二叉树,新的二叉树的根结点为新增加的结点,其权值为左右子树的权值之和。
3):删除与插入:在森林集合F中删除已选取的两棵根的权值最小的树,同时将新构造的二叉树加入到森林集合F中。
4):重复2)和3)步骤,直至森林集合F中只含一棵树为止,这颗树便是哈夫曼树,即最优二叉树。由于2)和3)步骤每重复一次,删除掉两棵树,增加一棵树,所以2)和3)步骤重复n-1次即可获得哈夫曼树。
下图展示了有4个叶子且权值分别为{9,6,3,1}的一棵最优二叉树的建立过程。

哈夫曼编码(编码译码都从根开始)
哈夫曼树的应用很广,哈夫曼编码就是其在电讯通信中的应用之一。广泛地用于数据文件压缩的十分有效的编码方法。其压缩率通常在20%~90%之间。
例:如果需传送的电文为 ‘ABACCDA’,它只用到四种字符,用两位二进制编码便可分辨。假设 A, B, C, D 的编码分别为 00, 01,10, 11,则上述电文便为 ‘00010010101100’(共 14 位),译码员按两位进行分组译码,便可恢复原来的电文。
能否使编码总长度更短呢?
实际应用中各字符的出现频度不相同,用短(长)编码表示频率大(小)的字符,使得编码序列的总长度最小,使所需总空间量最少
数据的最小冗余编码问题
在上例中,若假设 A, B, C, D 的编码分别为 0,00,1,01,则电文 ‘ABACCDA’ 便为 ‘000011010’(共 9 位),但此编码存在多义性:可译为: ‘BBCCDA’、‘ABACCDA’、‘AAAACCACA’ 等。
译码的惟一性问题
要求任一字符的编码都不能是另一字符编码的前缀,这种编码称为前缀编码(其实是非前缀码)。 在编码过程要考虑两个问题,数据的最小冗余编码问题,译码的惟一性问题,利用最优二叉树可以很好地解决上述两个问题
以电文中的字符作为叶子结点构造二叉树。
将二叉树中结点引向其左孩子的分支标 ‘0’,引向其右孩子的分支标 ‘1’; 每个字符的编码即为从根到每个叶子的路径上得到的 0, 1 序列。如此得到的即为二进制前缀编码。

编码: A:0, C:10,B:110,D:11
任意一个叶子结点都不可能在其它叶子结点的路径中。
用哈夫曼树设计总长最短的二进制前缀编码
假设各个字符在电文中出现的次数(或频率)为 wi ,其编码长度为 li,电文中只有 n 种字符,则电文编码总长为:

设计电文总长最短的编码,设计哈夫曼树(以 n 种字符出现的频率作权),
由哈夫曼树得到的二进制前缀编码称为哈夫曼编码
例:如果需传送的电文为 ‘ABCACCDAEAE’,即:A, B, C, D, E 的频率(即权值)分别为0.36, 0.1, 0.27, 0.1, 0.18,试构造哈夫曼编码。

编码: A:11,C:10,E:00,B:010,D:011 ,则电文 ‘ABCACCDAEAE’ 便为 ‘110101011101001111001100’(共 24 位,比 33 位短)。

电文为 “1101000” ,译文只能是“CAT”
#include<stdio.h>
#include<string.h>
#define MAXNODE 20
#define leafNum 3 //叶子节点数
#define nodeNum (2*leafNum-1) //总节点数 根据二叉树性质,n0=n2+1
#define MAXVALUE 99999
#define BITMAX 20//编码最大长度
typedef struct HTree
{
int weight;
char ch;
int parent,lchild,rchild;
}HTree;
typedef struct HCode
{
int bit[BITMAX];
int start;
char ch;
}HCode;
void select(HTree tree[],int newNum,int *node1,int *node2)//因为要返回两个值,将这两个值的
{
//找到第一小和第二小的,并将两者返回
int small1,small2;
*node1=*node2=0;
small1=small2=MAXVALUE;
int i;
for(i=0;i<newNum;i++)
{
if(tree[i].weight<small1)
{
small2=small1;
small1=tree[i].weight;
*node2=*node1;
*node1=i;
}
else if(tree[i].weight<small2)//一不满足了才会走到这里,
//也就是说此时在大于small1的里面找最小的
{
small2=tree[i].weight;
*node2=i;
}
}
}
void createHTree(HTree tree[])
{
int i,j;
int node1,node2;
int w;
char ch;
for(i=0;i<nodeNum;i++)
{
tree[i].weight=0;
tree[i].parent=-1;
tree[i].lchild=-1;
tree[i].rchild=-1;
}
printf("共有%d个字符\n ",leafNum);
for(i=0;i<leafNum;i++)
{
printf("请输入第%d个字符和权值",i+1);
scanf("%c%d",&ch,&w);
getchar();
tree[i].ch=ch;
tree[i].weight=w;
}
for(i=leafNum;i<nodeNum;i++)//构造虚拟节点,有m-n个
{
select(tree,i,&node1,&node2);
tree[node1].parent=i;
tree[node2].parent=i;
tree[i].lchild=node1;
tree[i].rchild=node2;
tree[i].weight=tree[node1].weight+tree[node2].weight;
}
}
void getCode(HTree tree[],HCode code[])
{
createHTree(tree);
int i;
HCode cd;
int tmp;
int par;
for(i=0;i<leafNum;i++)
{
cd.start=leafNum;// //对于有n个叶子节点的赫夫曼树,各叶子节点的编码长度最长不超过n-1
tmp=i;
cd.ch=tree[i].ch;
par=tree[i].parent;
while(par!=-1)//如果没到根结带
{
cd.start--;
if(tree[par].lchild==tmp)
cd.bit[cd.start]='0';
else
cd.bit[cd.start]='1';
tmp=par;//替换上层节点
par=tree[tmp].parent;
}
code[i]=cd;
// printf(&cd[start]);
}
}
void print(HTree tree[],HCode code[])
{ int i;
for ( i= 0; i < leafNum; i++)
{
printf("%c\n",tree[i].ch);
printf("%d\n",code[i].bit);
}
}
int main()
{
HTree tree[MAXNODE];
HCode code[MAXNODE];
memset(tree,0,sizeof(tree));
memset(code,0,sizeof(code));
createHTree(tree);
getCode(tree,code);
print(tree,code);
return 0;
}
参考资料:
http://blog.csdn.net/tanswer_/article/details/52794335
https://www.cnblogs.com/kubixuesheng/p/4397798.html
http://blog.csdn.net/qq_29187355/article/details/71247791




 浙公网安备 33010602011771号
浙公网安备 33010602011771号